
3 Skaitiniai metodai vienam kintamajam
Svarbiausios vieną kintamąjį aprašančios statistikos ir kitos skaitinės suvestinės pateiktos pav. 3.1.

3.1 Imties dydis
Imties dydis – tai imtyje esančių elementų (pvz., tiriamųjų, pacientų, stebėjimų ar pan.) skaičius.
Imties dydį reiktų nurodyti visais atvejais: ir kai tiriame vieną, ir kai – daugiau nei vieną kintamąjį.
Imties dydis yra absoliutusis dydis, apibūdinantis į analizę patekusių elementų skaičių, tad kitaip nei sveikuoju skaičiumi jo nurodyti ir neišeitų. Bet nagrinėjant grupių bei pogrupių dydžius, juos galima apibūdinti įvairesniais būdais. Apie tai bus rašoma poskyryje 3.3. Bet prieš tai pakalbėkime apie trūkstamas reikšmes.
3.2 Trūkstamų reikšmių skaičius
3.2.1 Trūkstamos reikšmės – kas tai?
Dirbdami su tikrais duomenimis neretai susiduriame su situacija, kai duomenų lentelėje kai kurių duomenų reikšmių tiesiog nėra. Tokiai situacijai apibūdinti sukurtas specialus terminas:
- Trūkstama reikšmė arba praleista reikšmė (angl. missing value) – tai nežinoma, negalima arba neegzistuojanti kintamojo reikšmė.
Dalis statistinės analizės metodų neduoda rezultatų, jei yra trūkstamų reikšmių. Pvz., kaip apskaičiuoti vidurkį, kai duomenyse yra bent viena nežinoma (t.y., bet kokia) reikšmė? Dėl to pačioje analizės pradžioje bei pertvarkius duomenis (tarkime, sujungus 2 duomenų lenteles) yra svarbu patikrinti, ar duomenyse yra/atsirado trūkstamų reikšmių.
Trūkstamų reikšmių buvimą reiktų tikrinti visada (ir kai tiriame vieną, ir kai – daugiau nei vieną kintamąjį), bet jei su šia charakteristika problemų nėra, tai apie tai mokslinio darbo analizės ataskaitoje įprastai nekalbama.
Prieš atlikdami aprašomąją statistiką, patikrinkite, ar jūsų duomenyse yra trūkstamų reikšmių.
Pilnieji stebėjimai (pilnieji atvejai; angl. complete cases) – tai duomenų lentelės eilučių (stebėjimų, atvejų) skaičius be trūkstamų reikšmių. Jei žiūrėsime į visas eilutes, lentelėje 3.1 yra 3 tokios eilutės: Nr. 1, 3 ir 5. Taigi, šis terminas apibūdina tik tuos atvejus, kuriuos galima naudoti analizei be jokių papildomų apdorojimų. Jei visos eilutės – pilnieji atvejai, vienos iš galimų problemų neturite.
NA) pavyzdys.| Eil.nr. | A | B | C | D |
|---|---|---|---|---|
| 1 | 0,2 | 4 | 2 | 124 |
| 2 | 0,4 | NA | NA | 185 |
| 3 | 0,5 | 6 | 5 | 132 |
| 4 | 0,3 | 1 | NA | 149 |
| 5 | 0,3 | 3 | 2 | 122 |
3.2.2 Kaip tikrinti dėl trūkstamų reikšmių?
Trūkstamų reikšmių paieška įprastai atliekama tokiu eiliškumu:
- patikrinama, ar duomenys apskritai turi bent vieną trūkstamą reikšmę;
- jei turi, nustatoma, kuriuose stulpeliuose ir koks skaičius;
- jei turi, įvertinama pilnųjų stebėjimų skaičius;
- jei reikia, atliekama išsamesnė trūkstamų reikšmių analizė (pvz., analizuojama, ar matomos kokios nors tendencijos, ar galima įtarti, kad visų trūkstamų reikšmių atsiradimo priežastis yra ta pati, o gal yra kelios priežastys).
Plačiau apie sudėtingesnę trūkstamų reikšmių analizę šiame kurse nesimokysime. Bet būtinai patikrinkite, ar trūkstamų reikšmių yra apskritai, o kai yra, tada nustatykite kur ir kiek.
Trūkstamų reikšmių paieškos pavyzdys pateiktas lentelėje 3.2.
| Kintamojo pavadinimas | NA skaičius | Pilnųjų stebėjimų skaičius pašalinus šioje eilutėje nurodytą kintamąjį |
|---|---|---|
| Eil.nr. | 0 ( 0.0%) | 3 (60.0%) |
| A | 0 ( 0.0%) | 3 (60.0%) |
| B | 1 (20.0%) | 3 (60.0%) |
| C | 2 (40.0%) | 4 (80.0%) |
| D | 0 ( 0.0%) | 3 (60.0%) |
* Stebėjimų skaičius iš viso 5, pilnieji stebėjimai – 3.
3.2.3 Žymėjimas
Tuščia reikšmė (pvz., tuščia teksto eilutė) ir trūkstama reikšmė yra skirtingi dalykai: tuščia reikšmė yra konkreti žinoma reikšmė (nors gal neįprasta), o trūkstama – nežinomas (tad galimai bet koks) duomuo. Įvedant duomenis, kartais pamirštama įrašyti reikšmę, todėl langelis lieka tuščias. Norint pažymėti, jog duomenų suvedimo specialistas nepadarė klaidos (nepamiršo įvesti), arba atkreipti dėmesį, naudojami specialūs simboliai ar žodžiai. Skirtinguose tyrimuose šis žymėjimas gali skirtis (pvz. lentelėje 3.3), sakykime:
- simboliai, kurių nėra tarp įprastinių reikšmių, tokie kaip „
?“ ar „–“; - specifiniai užrašai, tokie kaip „
UNKNOWN“ (lt. nežinoma), „(nežinoma)“, „(neatlikta)“, „(netirta)“, „N/A“ ar „n.a.“ (angl. not available); - aiškiai į akis krentančios negalimos reikšmės, sakykime,
-99ar-1tiriamojo amžių nurodančiame stulpelyje; - kompiuterinės programos dažnai turi joms standartinius žymėjimus, pvz., „
NA“ (programa „R“), „#N/A“ (programa „Excel“), „n/a“ ar panašiai (pavyzdys lentelėje 3.4).
Šiame vadovėlyje trūkstamas reikšmes įprastai žymėsime NA.
Idealu, kai trūkstamų reikšmių žymėjimo būdas įvardintas duomenų lentelės ar kintamųjų aprašyme. Kitu atveju gali būti sunku jas atpažinti.
| ID | Amžius | Svoris, kg | Lytis | Tyrimo rezultatas | Kraujo grupė |
|---|---|---|---|---|---|
| 1 | 23 | 68 | Vyras | - | B |
| 2 | -1 | 80 | Vyras | Neigiamas | ? |
| 3 | 35 | -99 | (nežinoma) | Teigiamas | 0 |
| 4 | 29 | 52 | Moteris | - | AB |
| 5 | -1 | -99 | Moteris | Neigiamas | AB |
NA. P.S.: vyrams mėnesinės nevyksta.| ID | Amžius | Svoris, kg | Lytis | Ar mėnesinės reguliarios? | Kraujo grupė |
|---|---|---|---|---|---|
| 1 | 23 | 68 | Vyras | NA | B |
| 2 | NA | 80 | Vyras | NA | NA |
| 3 | 35 | NA | NA | NA | 0 |
| 4 | 29 | 52 | Moteris | Taip | AB |
| 5 | NA | NA | Moteris | Ne | AB |
3.2.4 NA atsiradimo priežastys
Keletas paaiškinimų, dėl ko gali atsirasti trūkstamos reikšmės:
- respondentas atsisakė atsakyti į vieną ar kelis klausimus, nors likusius atsakymus pateikė;
- prietaisas, sugedo, tad vieno iš 5 tyrimo pakartojimų su keliais tiriamaisiais neatlikome. Likę tiriamieji buvo ištirti pilnai;
- tam tikro tipo duomenis surinkti sunku (pvz., dėl didelės kainos ar galimybių stokos), todėl jie renkami tik daliai tiriamųjų;
- konkretus tiriamasis tos savybės neturi, pvz., vyras į klausimą „kada jums paskutinį kartą vyko mėnesinės“ atsakyti negali;
- suvedant, į vieną ar kelis lentelės langelius duomenys nesuvesti (tyrėjas buvo pavargęs) arba įvesta reikšmė neišsisaugojo;
- skaičiavimų rezultatas – negalima reikšmė (pvz., atliekant dalybą iš nulio ar logaritmuojant neigiamus skaičius rezultatas užrašomas kaip trūkstama, t.y., negalima, reikšmė);
- sujungiant kelis duomenų rinkinius, kai skirtingi rinkiniai turi informacijos tik apie dalį tiriamųjų;
- pertvarkant duomenis, pvz., kai duomenys pertvarkomi iš plačiojo formato į ilgąjį (apie tai plačiau mokysitės praktinių užsiėmimų metu);
- dėl kitų priežasčių.
3.2.5 Ką daryti su NA?
Kaip galima elgtis su trūkstamomis reikšmėmis:
- Surasti ir įrašyti tikrąsias reikšmes, jei tai įmanoma.
- Pašalinti visą eilutę, kurioje yra bent viena trūkstama reikšmė:
- tokiu atveju mažėja imties dydis, o tai ne visada priimtina;
- jei eilutėje tik trūkstamos reikšmės – tai tuščia eilutė ir ją būtina pašalinti;
- jei trūkstama reikšmė atsirado dėl techninių priežasčių ir tai dirbtinai padidina lentelės eilučių skaičių, tada tokias eilutes pašalinti privaloma.
- Pašalinti stulpelį, kur yra trūkstamų reikšmių:
- tokiu atveju mažėja kintamųjų skaičius, o tai ne visada priimtina;
- jei analizei reikalingi/naudingi ne visi stulpeliai, tada kai kuriuos stulpelius galime šalinti;
- jei stulpelyje beveik visos reikšmės trūkstamos (pvz., >90%), tada, tikėtina, tokį stulpelį reiktų pašalinti. Nebent jame iš tiesų svarbi informacija.
- Naudoti metodus, kurie patys moka susidoroti su trūkstamomis reikšmėmis.
- Laikinai ignoruoti trūkstamas reikšmes, jei tai įmanoma. Pvz., skaičiuojant vidurkį laikinai pašalinti trūkstamas reikšmes ir skaičiavimus atlikti su likusiomis.
- Užpildyti (angl. impute) trūkstamas reikšmes:
- įrašyti konkrečią reikšmę. Pvz., jei žinoma, jog trūkstama reikšmė reiškia, kad tiriamųjų nebuvo, tada galime įrašyti 0. Kartais žinome, kad galima įrašyti kitokį skaičių;
- įrašyti reikšmę, apskaičiuotą iš duomenų. Pvz., stulpelio vidurkio ar medianos reikšmė;
- sumodeliuoti (bandyti atspėti) pagal kitų stulpelių reikšmes:
- pirmiausia pagal eilutes, kur nėra trūkstamų reikšmių, apmokomas modelis;
- po to tas modelis bando atspėti, ką įrašyti vietoje trūkstamų reikšmių.
- Pagal stulpelį su trūkstamomis reikšmėmis susikurti indikatorinį stulpelį (žr. lentelėje 3.5). Naujajame stulpelyje:
1arbataipreiškia, kad pradinis stulpelis turėjo trūkstamą reikšmę;0arbanereiškia, kad buvo konkreti žinoma reikšmė.
Koncentracija) ir naujas indikatorinis stulpelis, rodantis, kurios jo reikšmės yra trūkstamos (Koncentracija nenustatyta).| Eil.nr. | Koncentracija | Koncentracija nenustatyta |
|---|---|---|
| 1 | NA | Taip |
| 2 | 8 | Ne |
| 3 | NA | Taip |
| 4 | NA | Taip |
| 5 | 5 | Ne |
| 6 | 2 | Ne |
Šiame kurse mes mokysimės suskaičiuoti, kiek kiekvienas stulpelis turi trūkstamų reikšmių, kai reikės – trūkstamas reikšmes ignoruoti arba pašalinti atitinkamas eilutes. Sudėtingesni metodai kurso metu nebus analizuojami ir čia pateikti tik dėl bendro išprusimo.
3.3 Dažniai
Dažnis (angl. frequency, žymėsime f) statistikoje – tai reikšmių skaičius arba pasikartojimo dažnumas. Pvz., sakinyje „tyrime dalyvavo penkiolika vyrų iš kurių 60% nevartoja kavos“ skaičiai „15“ ir „60%“ yra dažniai. Pasikartoti gali tiriamieji, reiškiniai, tam tikros reikšmės, kategorijos, reikšmių grupės, reikšmių intervalai bei jų kombinacijos. O terminai „pasitaikymo dažnumas“ arba „skaičius“ neretai gali būti vartojami kaip termino „dažnis“ sinonimai.
Dažnis (statistikoje) = (reikšmės) pasikartojimų dažnumas.
Atsako į klausimą „Kiek?“(Kiek vienetų? Kiek procentų? Kuri dalis?)
Nulinis dažnis – tai situacija, kai reikšmė (kategorija, kombinacija, intervalas) nei karto nepasikartojo (f = 0).
3.3.1 Žymėjimai
Dažnius galima suskirstyti pagal keletą kriterijų. Prieš kalbėdami apie juos, susipažinkime su poskyriuose apie dažnius naudojamais matematiniais žymėjimais:
- n – visų duomenų eilutės elementų skaičius (imties dydis),
- k – skirtingų reikšmių skaičius (k ≤ n),
- i – reikšmės eilės numeris unikalių reikšmių sąraše (1 ≤ i ≤ k),
- x_i – viena iš galimų skirtingų (unikalių) duomenų reikšmių (i-toji),
- f_i – absoliutusis dažnis (i-tosios unikalios reikšmės),
- f_{i}^{\rm{sukauptasis}} – sukauptasis absoliutusis dažnis (i-tosios unikalios reikšmės).
3.3.2 Absoliutieji ir santykiniai dažniai
Pagal tai, ar atsižvelgiama į visumą (pvz., grupės dydį), dažniai būna:
absoliutieji dažniai (angl. absolute frequencies) – tai grupės narių ar reikšmės pasikartojimų skaičius, išreikštas kaip sveikasis skaičius, priklausantis intervalui nuo 0 iki +\infty. Pvz., „10 žaliaakių.“ Matematiškai griežtesnis apibrėžimas: absoliutusis reikšmės x_i dažnis f_i – tai skaičius, nurodantis, kiek kartų reikšmė x_i pasikartojo duomenų eilutėje.
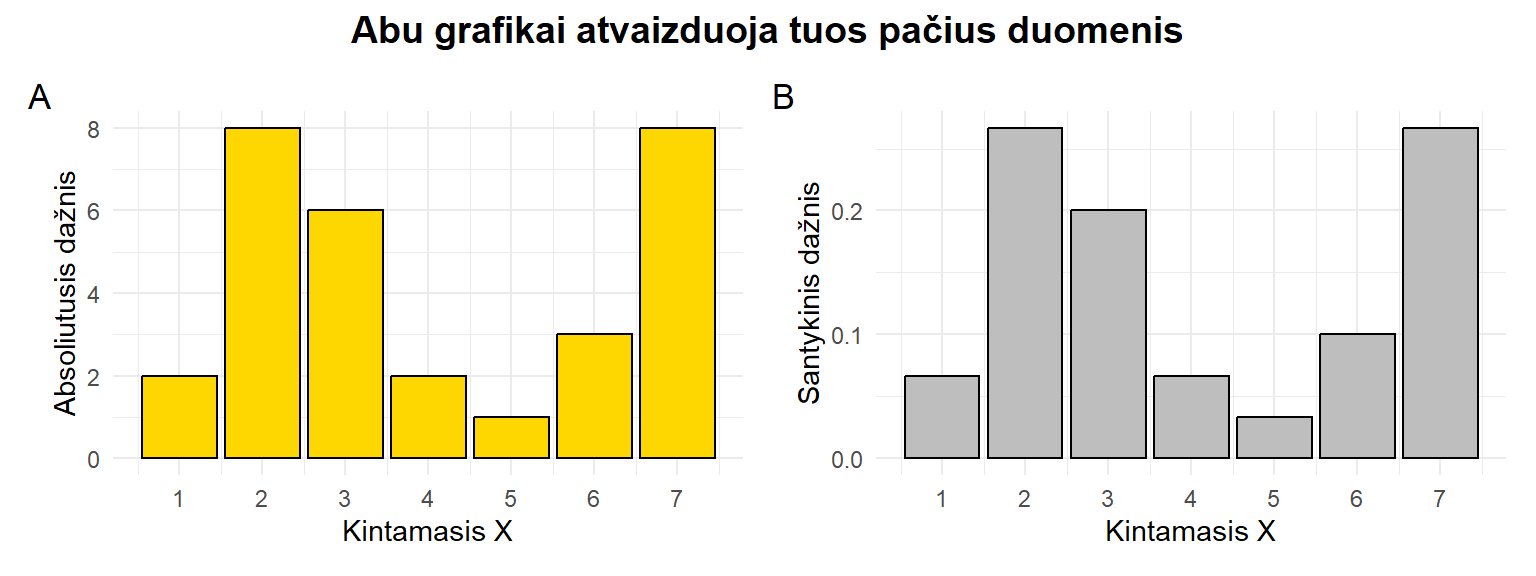
santykiniai dažniai (angl. relative frequencies) – tai pagal grupės dydį sunormuoti dažniai, parodantys, kuri visumos dalis yra apibūdinama. Matematiškai griežčiau galime apsibrėžti, kad kintamojo reikšmės santykinis dažnis \frac{f_i}{n} – tai skaičius, nurodantis, kurią duomenų sekos dalį sudaro reikšmė x_i.
Santykiniai dažniai gali būti pateikti kaip:
proporcijos, arba dalys, (angl. fraction) – tai santykiniai dažniai, įprastai išreikšti kaip skaičius tarp 0 ir 1 \left(0 \le \frac{f_i}{n} \le 1 \right). Pvz., „3/10 dalyvių buvo aukštesni nei 175 cm“; čia \frac{3}{10}=0{,}3 ir yra apibūdinamų tiriamųjų dalis. Proporcijos dažniau naudojamos matematiniuose skaičiavimuose (ypač tarpiniuose).
procentai (procentinė dalis, angl. percentage) – tai procentais išreikšti santykiniai dažniai, pvz., „30% dalyvių buvo aukštesni nei 175 cm“. Procentai dažniau nurodomi galutiniam vartotojui skirtuose dokumentuose, pvz., straipsniuose ar tyrimų ataskaitose.
Jei pateikti absoliutieji dažniai, tada iš jų galime apsiskaičiuoti bendrą imties dydį. Jei pateikti santykiniai dažniai, tada žinodami imties dydį galime bent apytiksliai apskaičiuoti absoliučiuosius dažnius. Kodėl tik apytiksliai? Nes neretai santykiniai dažniai pateikiami suapvalintai.
3.3.3 Sukauptieji dažniai
Pagal tai, ar skaičiavimuose atsižvelgiama į prieš tai buvusius dažnius, dažniai būna:
- paprastieji – kai į kitus dažnius neatsižvelgiama. Tai ir yra įprastiniai mums geriausiai žinomi dažniai. Aprašydami paprastuosius dažnius žodžio „paprastasis“ neminime. Tokių dažnių pvz.:
- 6, 2, 4 (absoliutieji dažniai);
- 20%, 10%, 70% (santykiniai dažniai).
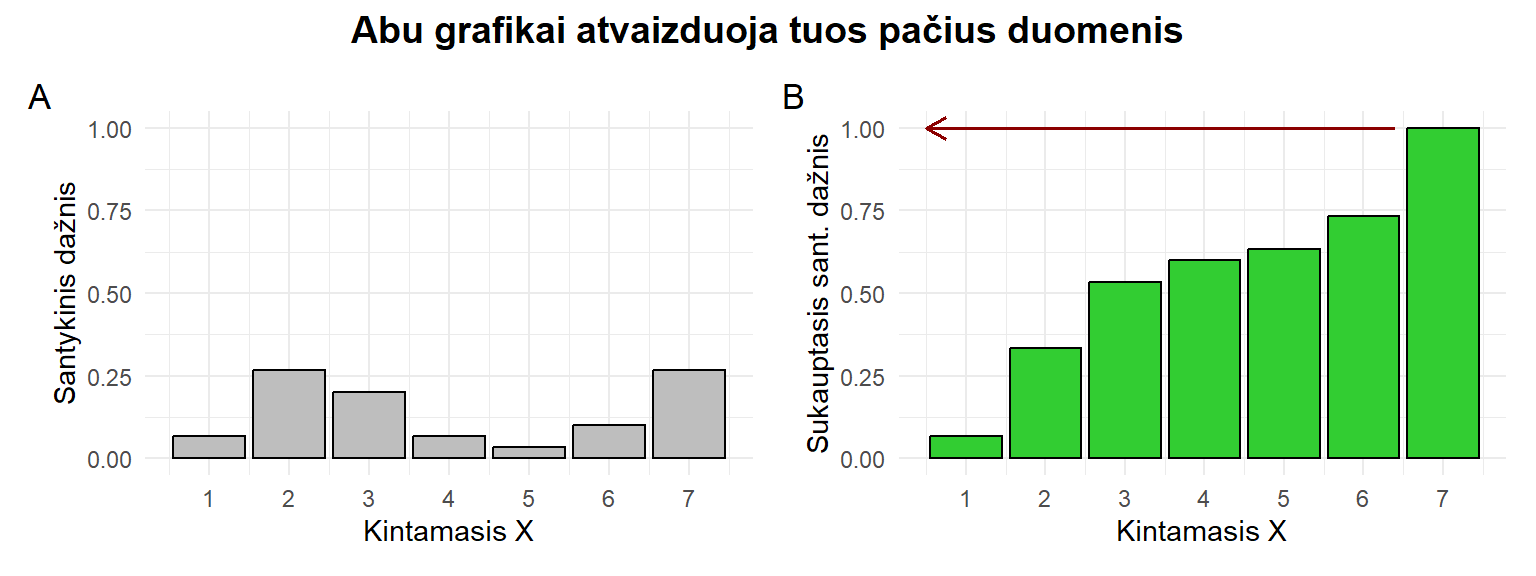
- sukauptieji1 (angl. cumulative) – kai, skaičiuojant reikšmės dažnį, pridedami prieš tai buvusių reikšmių dažniai. f_i^{\rm{sukauptasis}} = \sum_{j=1}^{i}f_j = f_1 + ...+f_i \tag{3.1} Sukauptieji gali būti tiek absoliutieji, tiek santykiniai dažniai. Įprastai sukauptieji dažniai yra prasmingi natūralią eilės tvarką turinčioms (pvz., kiekybinėms diskrečiosioms) reikšmėms, kurioms galima sudaryti variacines sekas. Tokių dažnių pvz.:
- 6, 8, 12 (t.y., 6, 6+2, 6+2+4; sukauptieji absoliutieji dažniai);
- 20%, 30%, 100% (t.y., 20%, 20+10%, 20+10+70%; sukauptieji santykiniai dažniai).
Kaip pastebite, sukauptieji dažniai yra didėjantys (arba bent jau nemažėjantys): f_i^{\rm{sukauptasis}} \le f_{i+1}^{\rm{sukauptasis}} \tag{3.2} O santykiniai dažniai susikaupia į 1, t.y., 100%: f_n^{\rm{sukauptasis}} = n \tag{3.3} \frac{f_n^{\rm{sukauptasis}}}{n} = 1 \tag{3.4}
3.3.4 Reikšmių intervalų dažniai
Pagal tai, ar skaičiuojami pavienėms reikšmėms, ar jų grupėms, dažniai skirstomi į:
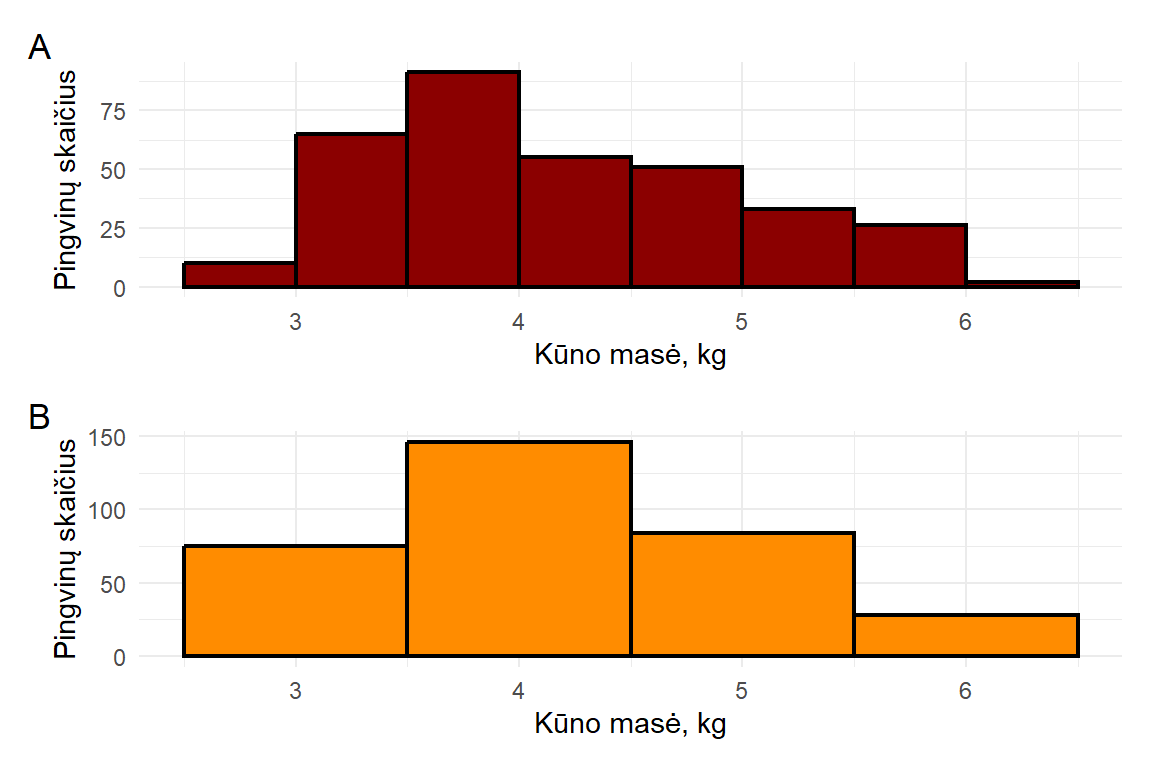
atskirų (pavienių) reikšmių dažnius – skaičiuojami kiekvienai reikšmei atskirai. Tai įprasta daryti diskrečiųjų savybių turintiems duomenims (pvz., nominaliesiems). Tačiau tolydiesiems, kuriems imtyje turėti sutampančių teoriškai yra nykstamai maža tikimybė, beveik visų pavienių reikšmių dažniai bus lygūs vienetui ir sutampančių reikšmių atsiras nebent dėl apvalinimo. Todėl dažnių skaičiavimui reikalinga kitokia metodika.
grupuotųjų reikšmių (angl. binned values), arba reikšmių intervalų, dažnius – kai pirmiausia apibrėžiami reikšmių intervalai ir taip reikšmės sugrupuojamos2, o tada suskaičiuojama, kiek reikšmių pateko į kiekvieną intervalą.
Intervalo kraštinių reikšmių bei pločio3 pasirinkimas – subjektyvus nuo tyrėjo, pasirinktos metodikos ar naudojamo įrankio nustatymų priklausantis dalykas. Tad šioje vietoje yra subjektyvumo. Įprasta pasirinkti vienodo pločio intervalus, kad jų dažnius būtų korektiška lyginti tarpusavyje. Įprastai norima, kad būtų bent 5 intervalai. Jei duomenų vidutiniškai daug, stengiamasi, kad į intervalą patektų bent 5-15 reikšmių, jei duomenų labai daug – intervale gali būti 30 ar daugiau reikšmių. Svarbiausia, kad pasirinktos intervalų savybės atskleistų tendencijas apie duomenis: per plačiuose intervaluose tendencijų nebesimato dėl per didelio suglotninimo, o per siauruose atsiranda daug triukšmo – pavienių išsišokančių reikšmių ar tuščių intervalų. Šie dalykai geriausiai matosi intervalus vizualizavus, tad apie tinkamo intervalų pločio pasirinkimą naudingiausia mokytis nagrinėjant temą apie histogramas.
Atskirų reikšmių dažnius vaizduojantis grafikas vadinamas stulpeline diagrama, o grupuotųjų reikšmių dažnius – histograma. Apie juos plačiau mokysimės skyriuje apie duomenų atvaizdavimą ir grafikus.
3.3.5 Dažnių lentelės
Suvestinėse įprasta pateikti ne pavienių reikšmių dažnius, o visas dažnių kolekcijas, vadinamas dažnių lentelėmis. Dažnių lentelė – tai galimos (unikalios) kintamojo reikšmės ir jų pasitaikymo dažnumą aibėje (pvz., imtyje) apibūdinantys statistiniai dažniai. Tad kai suskaičiuojame ir užrašome, kiek kartų kiekviena kintamojo reikšmė pasikartojo, gauname dažnių lentelę (pav. 3.6).

Reikšmės dažnių lentelėse gali būti:
- atskiros reikšmės (pvz., kategorijų pavadinimai, kai tiriami kategoriniai duomenys, arba pavienės skaitinės reikšmės, kai galimų reikšmių mažai, sakykime, iki 20);
- reikšmių intervalai (kai analizuojami kiekybiniai – ypač tolydieji – kintamieji, kurie turi daug skirtingų galimų reikšmių);
- reikšmių grupės (kai dalis reikšmių apjungiamos į vieną kategoriją, pvz., „pirmakursiai“ ir „visi kiti“);
- reikšmių kombinacijos (kai analizuojami keli kintamieji ir skaičiuojami kiekvienos tų kintamųjų reikšmių kombinacijos dažniai).
Pagal dažnius lentelės gali būti absoliučiųjų, santykinių, sukauptųjų santykinių ir pan. Vienoje lentelėje gali būti ir kelių rūšių dažniai.
Pateiksime kelis dažnių lentelių pavyzdžius.
Pingvinų rūšis Skaičius
1 Adelie 146
2 Chinstrap 68
3 Gentoo 119Pingvinų rūšis
Adelie Chinstrap Gentoo
146 68 119 | Spalva | Skaičius | Dalis |
|---|---|---|
| Juoda | 35 | 0.354 |
| Žalia | 11 | 0.111 |
| Geltona | 30 | 0.303 |
| Raudona | 23 | 0.232 |
Dažnių lentelės – tai pagrindinis kategorinių duomenų statistinio apibendrinimo būdas.
3.4 Centro padėtis
Duomenų centro padėties4 (angl. central tendency) charakteristikos apibūdina, kurioje kintamojo reikšmių srities vietoje (pvz., ties kuria liniuotės žyma, jei matuojamas ilgis) reiktų tikėtis rasti tipinę (centrinę) reikšmę. T.y., nusako, kur yra kintamojo reikšmių centras. Priklausomai nuo duomenų savybių, vienais atvejais „tikrąjį“ centrą tiksliau apibūdina vienos charakteristikos, kitais – kitos.
Duomenų centrą privaloma nurodyti apibūdinant kiekybinius kintamuosius. Galutinėje ataskaitoje įprasta nurodyti tik vieną (tinkamiausią) duomenų centro rodiklį.
3.4.1 Aritmetinis vidurkis
Aritmetinis vidurkis (žymėsime \overline{x}, M, angl. arithmetic mean arba average) – tai tarsi visų reikšmių „svorio“ centras, ties kuriuo išlaikomas balansas tarp mažų ir didelių reikšmių.

Imties vidurkis (statistika) apskaičiuojamas pagal formulę 3.5. Generalinės aibės vidurkis (parametras) dažnai žymimas \mu ir apskaičiuojamas pagal analogišką formulę.
\overline{x} = \frac{1}{n} \sum^n_{i=1}x_i = \frac{x_1+x_2+...+x_n}{n} \tag{3.5}
Žymėjimai: \overline{x} – imties vidurkis, n – imties dydis, x – duomenų seka, x_i – i-toji sekos reikšmė.
Aritmetinis vidurkis tinka, kai duomenys pasiskirstę simetriškai (pvz., pagal normalųjį skirstinį) ir yra be didelių (asimetriškų) išskirčių. Kai imtis maža, net viena smarkiai nuo centro nutolusi reikšmė gali ženkliai paslinkti „svorio centro“ (vidurkio) padėtį į nutolusios reikšmės pusę.
Vidurkį taip pat renkamės, jei taikome parametrinius metodus.
Jei duomenų savybės leidžia, centrui apibūdinti įprastai rinkitės aritmetinį vidurkį.
Iš visų centro padėties statistikų dažniausiai naudojamas aritmetinis vidurkis, nes jį lengva interpretuoti ir jis turi geras matematines ir statistines savybes, įskaitant šias:
- apskaičiavimas palyginus paprastas;
- naudoja visas kintamojo reikšmes, todėl reprezentuoja visą imtį;
- turint kelių grupių vidurkius ir grupių dydžius, galima gauti bendrą vidurkį;
- visas duomenų reikšmes padauginus iš, padalinus iš, pridėjus prie ar atėmus iš tos pačios konstantos analogiškai pasikeičia ir pats vidurkis;
- didelėms imtims imties vidurkis linkęs gerai atitikti GA vidurkį (didžiųjų skaičių dėsnis);
- vidurkis pats linkęs skirstytis normaliai, nors pradinių duomenų skirstinys gali nebūti normalusis (jam galioja centrinė ribinė teorema)5.
Vidurkio trūkumai (lyginant su moda ar mediana):
- jį labiau veikia asimetriškai nukrypusios vertės (išskirtys);
- jis yra jautresnis skirstinio asimetrijos laipsnio pokyčiams.
Aritmetinis (kaip ir geometrinis, harmoninis ar nupjautasis) vidurkis gali būti apskaičiuotas tik kiekybinių savybių turintiems duomenims. Vidurkio matavimo vienetai yra tokie patys kaip duomenų, kuriems jis skaičiuojamas.
Pavyzdys 3.1 Duota seka (masė kilogramais): 9, 4, 5. Jos aritmetinis vidurkis:
\overline{x} = \frac{x_1+x_2+x_3}{n} = \frac{9+4+5}{3} = 6 ~ kg
Pavyzdys 3.2 Duotos 3 sekos – aukštis centimetrais. Dvi paskutinės turi po vieną išskirtį (labai didelę reikšmę):
- Seka I: 1, 2, 3, 5, 5, 6, 6, 6, 8, 8 (cm), n = 10.
- Seka II: 1, 2, 3, 5, 5, 6, 6, 6, 8, 88 (cm), n = 10.
- Seka III: 1, 2, 3, 5, 6, 6, 6, 8, 188 (cm), n = 9.
Šios sekos bus naudojamos pavyzdžiuose.
Pavyzdys 3.3 Naudojami pavyzdžio 3.2 duomenys.
- Sekai I: \overline{x} = 5 cm.
- Sekai II: \overline{x} = 13 cm (viena nukrypusi reikšmė turi daug įtakos).
- Sekai III: \overline{x} = 25 cm (buvo dar labiau nukrypusi reikšmė).
3.4.2 Nupjautasis vidurkis
Nupjautasis vidurkis (angl. trimmed mean) – tai vidurkis, apskaičiuotas pašalinus tam tikrą dalį didžiausių ir mažiausių reikšmių6. Naudojant šį vidurkį privalu nurodyti, kuri dalis reikšmių bus „nupjaunama“ iš kiekvienos pusės (pvz. „10% nupjautasis vidurkis“). Įprastai atmetama po 5-25% reikšmių. O 50% nupjautuoju aritmetiniu vidurkiu gali būti laikoma mediana.
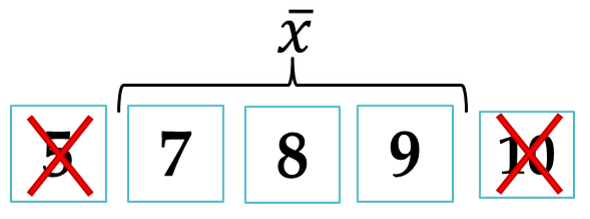
Įprastai terminas „nupjautasis vidurkis“ reiškia „nupjautasis aritmetinis vidurkis“. Šis aritmetinio vidurkio variantas atsparesnis išskirtims nei pats vidurkis (nes jos tiesiog į skaičiavimus neįtraukiamos).
Pavyzdys 3.4 Naudojant 10% nupjautąjį vidurkį prieš skaičiavimus pašalinama po 10% iš kiekvienos pusės. Pirmais dviem atvejais po 1 reikšmę (pabraukta):
- Sekai I (1, 2, 3, 5, 5, 6, 6, 6, 8, 8 cm):
\overline{x}_{10\% ~ nupj.} = 5,125 cm. - Sekai II (1, 2, 3, 5, 5, 6, 6, 6, 8, 88 cm):
\overline{x}_{10\% ~ nupj.} = 5,125 cm.
Paskutiniu – nei viena reikšmė nepašalinta, nes 10% nesusidarė (rezultatas sutampa su įprasto aritmetinio vidurkio atveju):
- Sekai III 1, 2, 3, 5, 6, 6, 6, 8, 188 cm):
\overline{x}_{10\% ~ nupj.} = 25 cm.
Mūsų kurso metu pakanka būti girdėjus apie šį vidurkio variantą.
3.4.3 Geometrinis vidurkis
Geometrinis vidurkis (x_G) – tai n-tosios eilės šaknis iš n reikšmių sandaugos:
x_G = \left({\prod^n_{i=1}x_i}\right)^\frac{1}{n} = \sqrt[{n}]{x_1 x_2 \cdots x_n} \tag{3.6}
Visos reikšmės turi būti teigiamos (x_i > 0).
Geometrinis vidurkis atsparesnis didelių reikšmių ir teigiamos asimetrijos įtakai nei aritmetinis vidurkis.
Jei pamenate logaritmų savybes (pvz., kad sandauga logaritmavus tampa sudėtimi), tai galite pastebėti, kad logaritminėje erdvėje geometrinis vidurkis taptų aritmetiniu vidurkiu.
Pavyzdys 3.5 Duota seka (masė kilogramais): 9, 4, 5. Geometrinis jos vidurkis:
x_G = \sqrt[{n}]{x_1 x_2 x_3} = \sqrt[3]{9·4·5} ≈ 5{,}65 ~ kg
Pavyzdys 3.6 Naudojami pavyzdžio 3.2 duomenys.
- Sekai I: x_G ≈ 4,28 cm.
- Sekai II: x_G ≈ 5,44 cm.
- Sekai III: x_G ≈ 5,98 cm.
Mūsų kurso metu pakanka būti girdėjus apie šį vidurkio variantą.
3.4.4 Harmoninis vidurkis
Harmoninis vidurkis (x_H) – tai atvirkštinių reikšmių atvirkštinis vidurkis:
x_H = \frac{n}{\sum^n_{i=1}\frac{1}{x_i}} = \frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}} \tag{3.7}
Visos reikšmės turi būti teigiamos (x_i > 0).
Harmoninis vidurkis tiksliau nei aritmetinis įvertina vidutinį greitį, kai jis skaičiuojamas nukeliauto kelio, o ne praėjusio laiko, atžvilgiu. Arba vidutinį kraujo tėkmės greitį, kai jis skaičiuojamas pratekėjusio kraujo kiekio, o ne tekėjimo trukmės, atžvilgiu. Tam, kad geriau suprastume šiuos teiginius, panagrinėkime tokius pavyzdžius:
- Automobilio greitis pirmą valandą buvo 40 km/h, o antrą – 60 km/h. Koks vidutinis automobilio greitis?
- Pastovus greitis buvo palaikomas tam tikrą laiko tarpą, tad šiam uždaviniui spręsti tinkamas aritmetinis vidurkis.
- Vidutinis greitis = \frac{(40 + 60)}{2} = 50 ~ km/h
- Automobilis pusę kelio važiavo 40 km/h greičiu, o kitą pusę kelio – 60 km/h. Koks vidutinis automobilio greitis?
- Pastovus greitis buvo palaikomas tam tikrą atstumą, tad šiam uždaviniui spręsti tinkamas harmoninis vidurkis.
- Vidutinis greitis = \frac{2}{1/40 + 1/60} = 48 ~ km/h
| Tinkamesnis harmoninis vidurkis | Matavimo vnt. | Tinkamesnis aritmetinis vidurkis |
|---|---|---|
| Skaičiuojant pagal km | km/h | Skaičiuojant pagal h |
| Skaičiuojant pagal ml | ml/min | Skaičiuojant pagal min |
| Skaičiuojant pagal kartus | kartai/s | Skaičiuojant pagal s |
Pavyzdys 3.7 Duota seka (masė kilogramais): 9, 4, 5. Harmoninis jos vidurkis:
x_H = \frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}} = \frac{3}{\frac{1}{9}+\frac{1}{4}+\frac{1}{5}} ≈ 5{,}35 ~ kg
Pavyzdys 3.8 Naudojami pavyzdžio 3.2 duomenys. Skaičiavimų pavyzdžiai:
- Sekai I: x_H ≈ 3,35 cm.
- Sekai II: x_H ≈ 3,48 cm.
- Sekai III: x_H ≈ 3,38 cm.
Mūsų kurso metu pakanka būti girdėjus apie šį vidurkio variantą.
3.4.5 Mediana
Mediana (žymėsime Md arba \tilde{x}, angl. median) – tai reikšmė, variacinę eilutę dalinanti į dvi pagal narių skaičių lygias dalis. Įprastai tai vidurinė variacinės eilutės reikšmė arba dviejų vidurinių reikšmių vidurkis.
- Mediana gali būti apskaičiuota natūralią reikšmių eilės tvarką turintiems duomenims: kiekybiniams ir ranginiams.
- Medianos matavimo vienetai tokie patys, kaip duomenų, kuriems ji skaičiuojama. Pvz., cm, g, santykiniai vienetai, dioptrijos ir pan.
- Tiksliau nei vidurkis įvertina duomenų centrą, jei:
- reikšmių pasiskirstymas smarkiai asimetriškas;
- yra didelių asimetriškų išskirčių.
- Nurodoma vietoje vidurkio, jei tolimesnėje analizėje naudojami neparametriniai metodai.
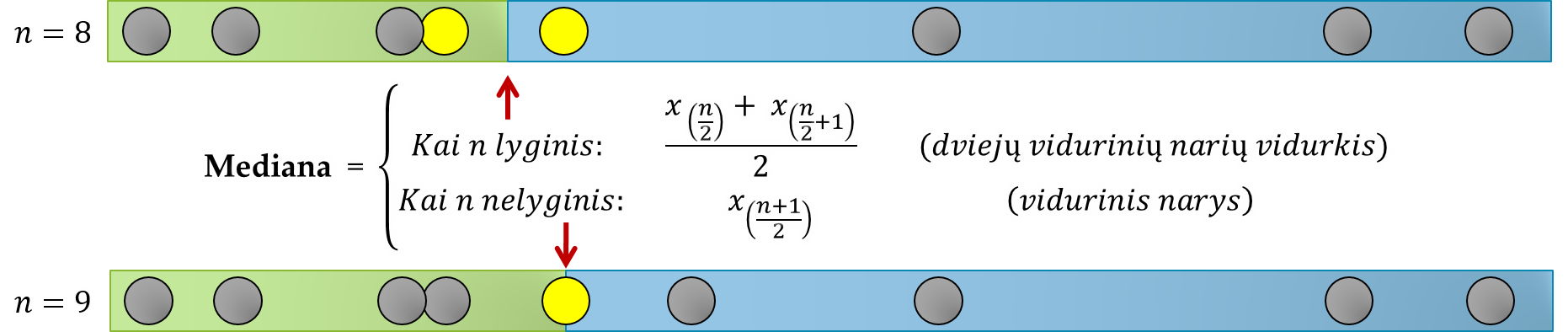
Iš kiekvienos medianos pusės turi būti po vienodą narių skaičių.
Pavyzdys 3.9 Skaičiavimų pavyzdžiai:
- Sekai I (1, 2, 3, 5, 5, 6, 6, 6, 8, 8 cm) Md = (5+6)/2 = 5,5 cm.
- Sekai II (1, 2, 3, 5, 5, 6, 6, 6, 8, 88 cm) Md = (5+6)/2 = 5,5 cm.
- Sekai III (1, 2, 3, 5, 6, 6, 6, 8, 188 cm) Md = 6 cm.
3.4.6 Moda
Moda (žymėsime Mo, angl. mode) – dažniausiai pasitaikanti duomenų eilutės reikšmė.
- Moda gali būti apskaičiuota diskrečiųjų savybių turintiems duomenims (žr. lentelėje 3.11);
- Tolydiesiems galima skaičiuoti tik juos sugrupavus į intervalus (atsiranda subjektyvumo).
- Matavimo vienetai – tokie patys, kaip duomenų, kuriems skaičiuojama moda.
- Iliustracijoje 3.10 tai X ašies („Grupė e“), o ne Y ašies (nurodytas dažnis) reikšmė.
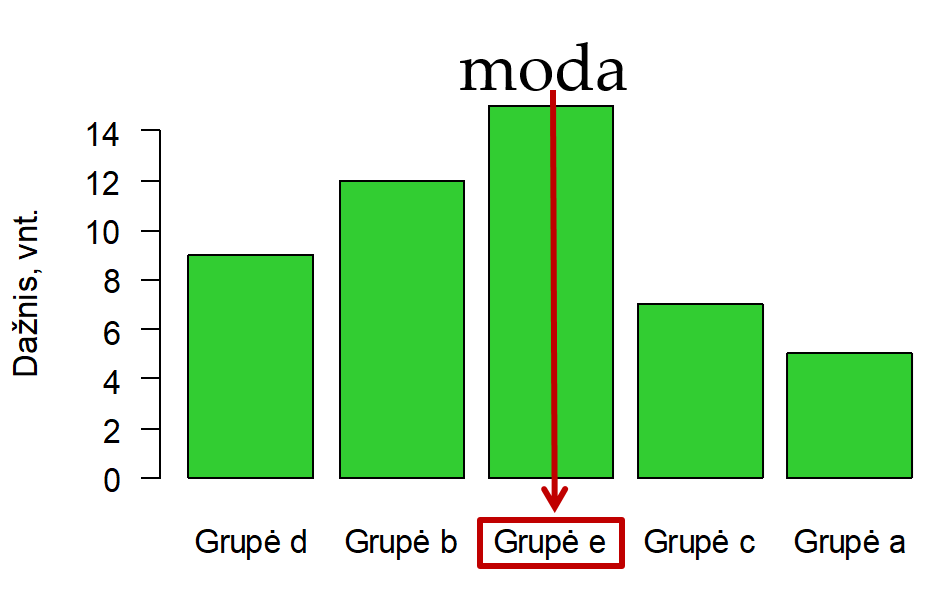
Duomenys gali modos neturėti (jei visos reikšmės pasitaiko vienodai dažnai), arba turėti kelias modas, jei, pvz., dvi reikšmės pasitaiko vienodai dažnai.
Pavyzdys 3.10 Skaičiavimų pavyzdžiai:
- Sekai I (1, 2, 3, 5, 5, 6, 6, 6, 8, 8 cm) Mo = 6 cm.
- Sekai II (1, 2, 3, 5, 5, 6, 6, 6, 8, 88 cm) Mo = 6 cm.
- Sekai III (1, 2, 3, 5, 6, 6, 6, 8, 188 cm) Mo = 6 cm.
3.5 Padėtis: sutartiniai taškai
Duomenyse be centro padėties yra ir kitokių sutartinių taškų, aprašančių duomenų padėtį reikšmių skalėje. Juos ir aptarsime šiame poskyryje. Bet prieš tai atkreipsiu dėmesį į tai, kaip į dalis galima dalinti variacinę seką.
3.5.1 Variacinės sekos dalinimas
Variacinę seką į lygias dalis galima padalinti skirtingais būdais (pav. 3.11):
- į lygias dalis pagal intervalo ilgį:
- tokiu atveju į kiekvieną intervalą pateks nebūtinai vienodas narių skaičius (pvz., sudarant histogramos stulpelius).
- į lygias dalis pagal reikšmių skaičių:
- tokiu atveju kiekvienas intervalas bus nebūtinai vienodo ilgio (pvz., skaičiuojant medianą ir kitus kvantilius).
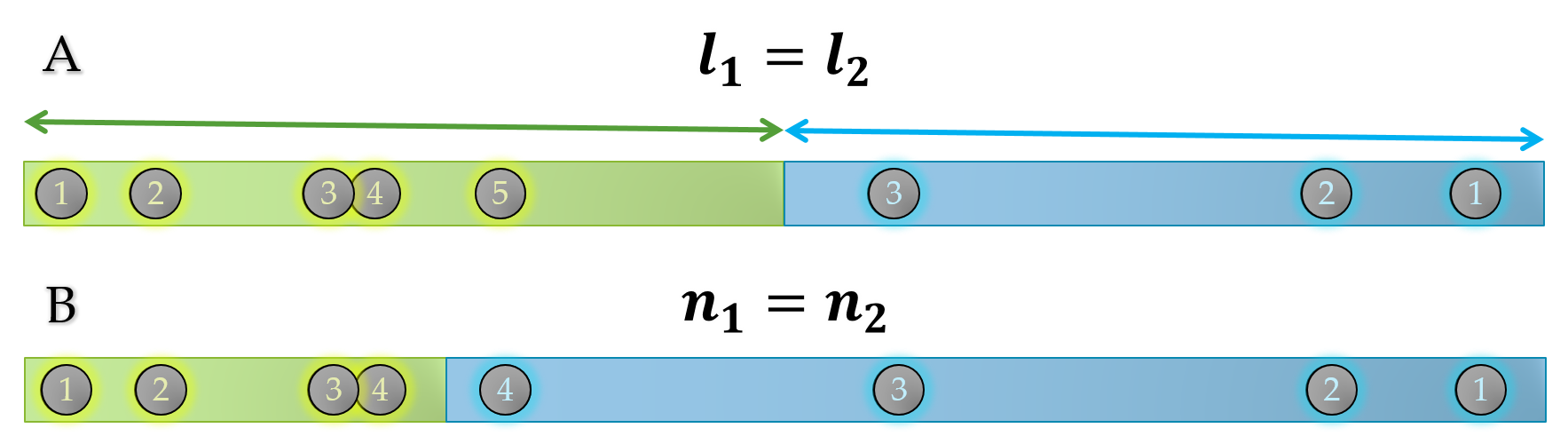
Atkreipkite dėmesį, kad galima dalinti ne tik į lygias, bet ir kitokias dalis (pvz., santykiu 30%:70%).
3.5.2 Didžiausia ir mažiausia reikšmė
Pirmasis variacinės sekos narys (x_{(1)}) yra mažiausia reikšmė (žymėsime x_{min}), o paskutinis (žymėsime x_{(n)}) – didžiausia (žymėsime x_{max}). Atliekant pradinę duomenų peržiūrą rekomenduoju pažvelgti į kelias (tarkime, penkias) didžiausias ir penkias mažiausias reikšmes bei įvertinti, kaip labai skiriasi greta esančios reikšmės. Jei skirtumai nedideli ar tokie, kaip tikitės, tai, matyt, šiuo požiūriu problemos nėra. O jei viena ar kelios reikšmės smarkiai nutolusios, tai gali indikuoti išskirtis arba asimetriją.
3.5.3 Kvantiliai
Reikšmės, kurios variacinę eilutę pagal narių skaičių dalija į tam tikro dydžio dalis, vadinamos kvantiliais (angl. quantiles). Juos galima įsivaizduoti kaip tam tikrus sutartinius taškus – duomenų padėtį apibūdinančias charakteristikas. Jei reiktų griežtesnio apibrėžimo, tai imties q-tosios eilės kvantilis (pažymėkime x_{(q)}, kur q \in [0; 1]) – yra konkreti duomenų eilutės reikšmė (arba dviejų reikšmių funkcija, pvz., vidurkis), kuri pagal narių skaičių variacinę eilutę dalina į dvi dalis: vienoje yra daugmaž q, kitoje – (1-q) narių.
Šiame kurse jau pristatytas ir bene plačiausiai naudojamas kvantilis, kurį galime žymėti q_{(0{,}5)}, kuris taip pat vadinamas antruoju kvartiliu, tad gali būti žymimas Q_2, ir turi specialų pavadinimą – mediana (Md): tai skaičius, variacinę eilutę pagal narių skaičių dalinantis į dvi lygias dalis santykiu 50%:50%. Pastaba: užrašas q_{(0{,}5)} = 63~kg reikštų, kad už vertę 63 kg yra 50% (nes žymima 0,5) mažesnių masių; kvantilio reikšmė yra 63 kg, o ne 50%.
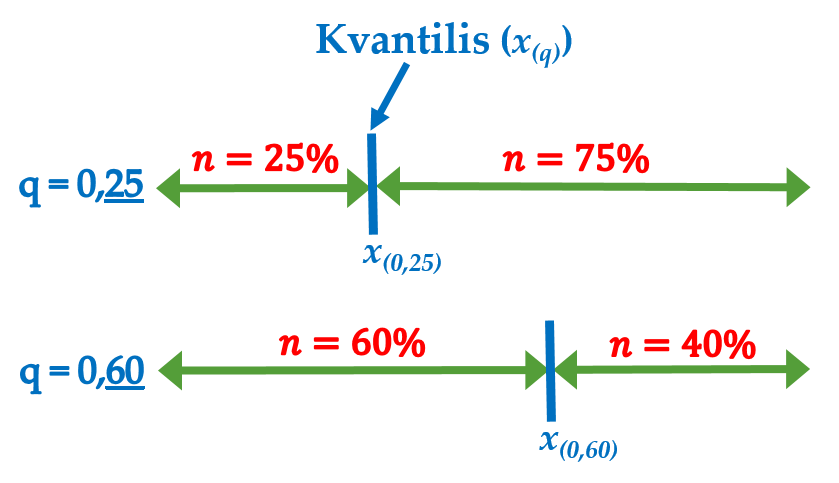
Dar keletas supaprastintų ir matematiškai ne visai tikslių paaiškinimų:
- imties kvantilis yra reikšmė, už kurią yra tam tikra dalis nedidesnių (diskrečiuoju atveju) arba tiesiog mažesnių (tolydžiuoju atveju) reikšmių:
- pvz., tokia grybo masė, už kurią yra 25% pagal masę nedidesnių grybų.
- imties kvantiliu (atsižvelgiant į 1 punkte minimus niuansus) galima laikyti reikšmę ties santykiniu sukauptuoju dažniu.
Jei randant kvantilį reikalingas tikslumas, naudokite lygtimis 3.8, 3.9, 3.10 aprašytą metodą.
Atkreipkite dėmesį, kad kvantilis matuojamas tais pačiais matavimo vienetais, kaip ir tiriamieji duomenys: jei matuojame ilgį centimetrais, tai kvantilis yra tam tikras ilgis centimetrais, jei masę kilogramais, tai ir kvantilis bus tam tikra masė kilogramais. Pvz., jei kvantilis x_{(q=0{,}2)} = 35 \mu m (įprastai bus žymimas tiesiog x_{(0{,}2)} = 35 \mu m), tai reiškia, kad 20% mūsų imtyje esančių tiriamųjų yra nedidesni (įprastai – mažesni) už 35 \mu m ir 80% didesni už šį kvantilį. Tai pat pastebėkite, jog skaičius q šalia kvantilio nurodo, kuri imties narių dalis yra nedidesnė už kvantilio reikšmę.
Kvantilių (kvartilių, procentilių) matavimo vienetai yra tokie patys, kaip duomenų, kuriems jie skaičiuojami.
Kvantilis yra pati bendriausia šio poskyrio sąvoka. Specifiniai kvantiliai turi ypatingus pavadinimus, pvz., kvartiliai ar procentiliai.
Kvartiliai (angl. quartiles) – tai kvantiliai, dalijantys variacinę seką į 4 pagal elementų skaičių lygias dalis. Įprastai žymimi Q_1, Md, Q_3.
- Yra 25% mažesnių reikšmių už Q_1 (t.y., x_{(0{,}25)});
- Yra 50% mažesnių reikšmių už Q_2 (t.y., Md, x_{(0{,}50)});
- Yra 75% mažesnių reikšmių už Q_3 (t.y., x_{(0{,}75)}).
Procentiliai – reikšmės, variacinę seką dalijančios į 100 pagal elementų skaičių lygių dalių.
Dažniausiai vartojamos kvantilius apibūdinančios sąvokos yra „kvantiliai“, „kvartiliai“ ir „procentiliai“. Bet dar egzistuoja ir terciliai, kvintiliai, heksiliai ir kitokie egzotiniai „-iliai“, kurių praktiškai niekur nepamatysite.
3.5.4 Kvantilių skaičiavimas
Kvantilių skaičiavimui yra sugalvota keletas būdų. Didelėms imtims rezultatai būna įprastai panašūs, o didesni skirtumai išryškėja esant mažesnėms imtims. Vieną iš būdų siūlau išmokti. Jo skaičiavimai susideda iš 3 etapų:
- Sudarome kintamojo variacinę seką: x_1, x_2, ..., x_n → x_{(1)}, x_{(2)}, ..., x_{(n)} \tag{3.8} Čia ( ~~~ ) – indeksas (eilės numeris) variacinėje sekoje, o → tiesiog žymi, kad pakeičiama duomenų eilės tvarka.
- Apskaičiuojame indeksą i: i = q × n \tag{3.9} Čia q – kvantilio eilė (nedidesnių reikšmių dalis, pvz., 0,30), n – imties ar grupės dydis.
- Randame kvantilį: x_q = \begin{cases} \text{ kai skaičius } i \text{ yra sveikasis: } ~~~~ \frac{x_{([i])} + x_{([i] + 1)}}{2} \\ \text{ kai skaičius } i \text{ nėra sveikasis: }~~~~~ x_{([i] + 1)} \end{cases} \tag{3.10} Čia [ ~~~] – sveikoji dalis, pvz., [2,2] → 2.
Pavyzdys 3.11 Skaičiavimų pavyzdžiai norint rasti x_{(0{,}3)}:
Sekai I (1, 2, 3, 5, 5, 6, 6, 6, 8, 8 cm):
i = q × n = 0{,}3 × 10 = 3
Rezultatas i yra sveikasis skaičius, tad: \begin{split} x_{0{,}3} & = \frac{x_{([i])} + x_{([i] + 1)}}{2} \\ & = \frac{x_{(3)} + x_{(3 + 1)}}{2} \\ & = \frac{3 + 5}{2} = 4~cm \end{split}Sekai II (1, 2, 3, 5, 5, 6, 6, 6, 8, 88 cm) x_{(0{,}3)} = 4 cm.
Skaičiavimai analogiški sekos II atvejui.Sekai III (1, 2, 3, 5, 6, 6, 6, 8, 188 cm): i = q × n = 0{,}3 × 9 = 2{,}7
Rezultatas i yra trupmeninis skaičius, tad: x_{(0{,}3)} = x_{([i] + 1)} = x_{(2+1)} = x_{(3)} = 3~cm
3.7 Skirstinio forma
Yra dvi pagrindinės duomenų skirstinio formą aprašančios statistikos: asimetrijos ir eksceso koeficientai.
3.7.1 Asimetrijos koeficientas
Asimetrijos koeficientas, g_1 (angl. skewness, trumpinama skew) – vertina skirstinio simetriškumą.
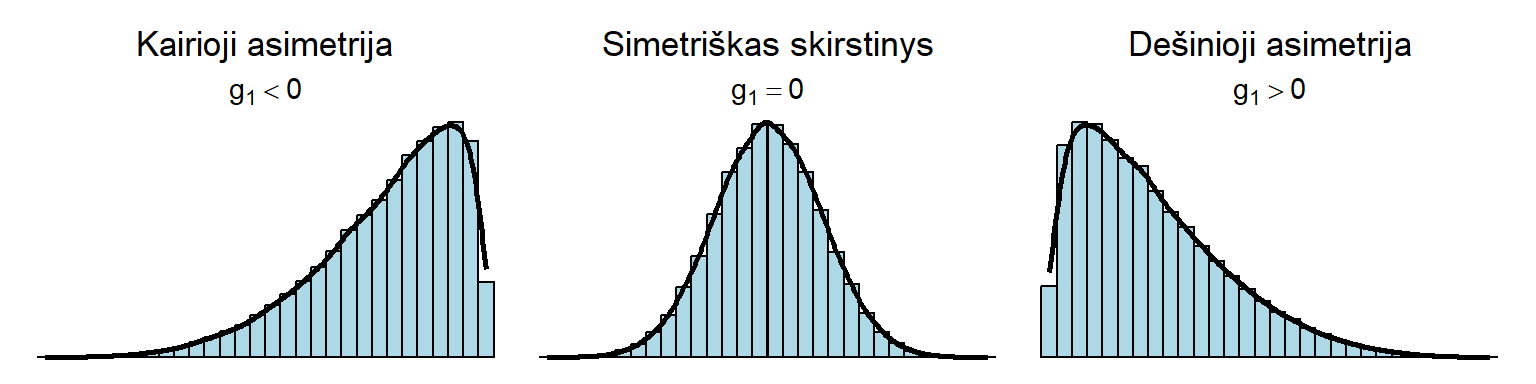
- Koeficiento ženklas nurodo asimetrijos kryptį (pav. 3.14):
- g_1 = 0 – ideali simetrija;
- g_1 < 0 – neigiama (kairioji) asimetrija;
- g_1 > 0 – teigiama (dešinioji) asimetrija. Pastarąją galima bandyti koreguoti logaritmuojant.
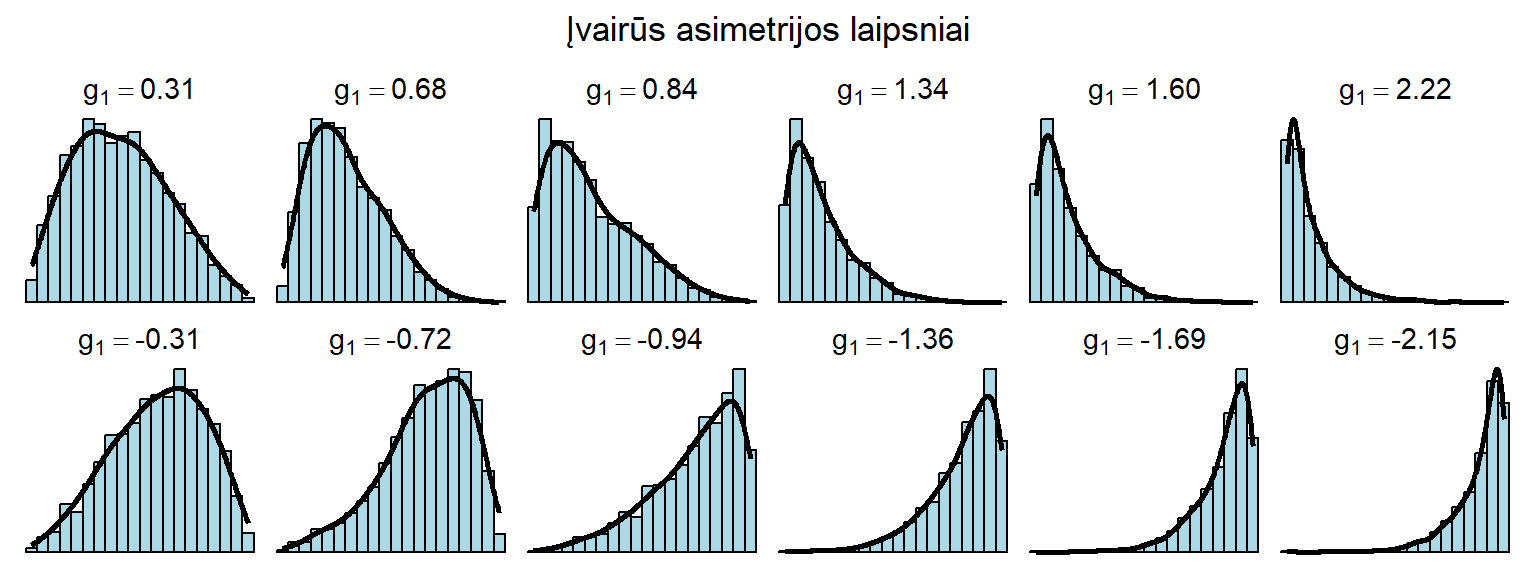
- Absoliutusis koeficiento dydis nurodo asimetrijos stiprumą (pav. 3.15).
- Koeficiento dydžio klasifikacija pagal (Bulmer 1979, p.65):
- g_1 = 0 – ideali simetrija;
- g_1 ∈ [-0{,}5; 0) ~ \cup ~ (0; +0{,}5] – maža asimetrija, beveik simetriška;
- g_1 ∈ [-1; -0{,}5) ~ \cup ~ (+0{,}5; +1] – vidutinio stiprumo asimetrija;
- g_1 ∈ (-∞; -1) ~ \cup ~ (+1; +∞) – stipri asimetrija.
- Koeficiento dydžio klasifikacija pagal (Hair ir kt. 2022, p.66):
- g_1 ∈ [-1; +1] – „puiku“;
- g_1 ∈ [-2; -1) ~ \cup ~ (+1; +2] – „priimtina“;
- g_1 ∈ (-∞; -2) ~ \cup ~ (+2; +∞) – „smarki nenormalumo indikacija“10
- Koeficiento dydžio klasifikacija pagal (Bulmer 1979, p.65):
3.7.2 Eksceso koeficientas
Užtenka būti girdėjus.
Eksceso koeficientas, g_2 (angl. excess kurtosis). Rodo skirstinio formos bukumą/smailumą lyginant su normaliuoju skirstiniu: ar dauguma duomenų taškų yra susitelkę ties keliomis reikšmėmis, ar išsisklaidę variacinėje eilutėje.
- g_2 = 0 – smailumas kaip normaliojo skirstinio;
- g_2 > 0 – centrinė kreivės dalis smailesnė, o duomenų sklaida apie vidurkį didesnė nei normaliosios kreivės;
- g_2 < 0 – centrinė kreivės dalis bukesnė, o duomenų sklaida apie vidurkį mažesnė nei normaliosios kreivės arba skirstinys yra keliaviršūnis.
3.8 Aprašomųjų statistikų parinkimas
3.8.1 Centro padėties rodiklio tinkamumas
Kiekybiniams duomenims dažniausiai naudojamos centro padėties charakteristikos – aritmetinis vidurkis arba mediana. Kai situacija leidžia (duomenys daugmaž simetriški, be didelių asimetriškų išskirčių arba analizei korektiškai pasirinkome parametrinius metodus), tada renkamės aritmetinį vidurkį. Kitu atveju – medianą. Galutinėje ataskaitoje (straipsnyje ar kitokiame darbe) pateikiamas tik vienas rodiklis, kuris labiausiai tinkamas tai situacijai.
Yra situacijų, kur geriau rinktis kitus rodiklius.
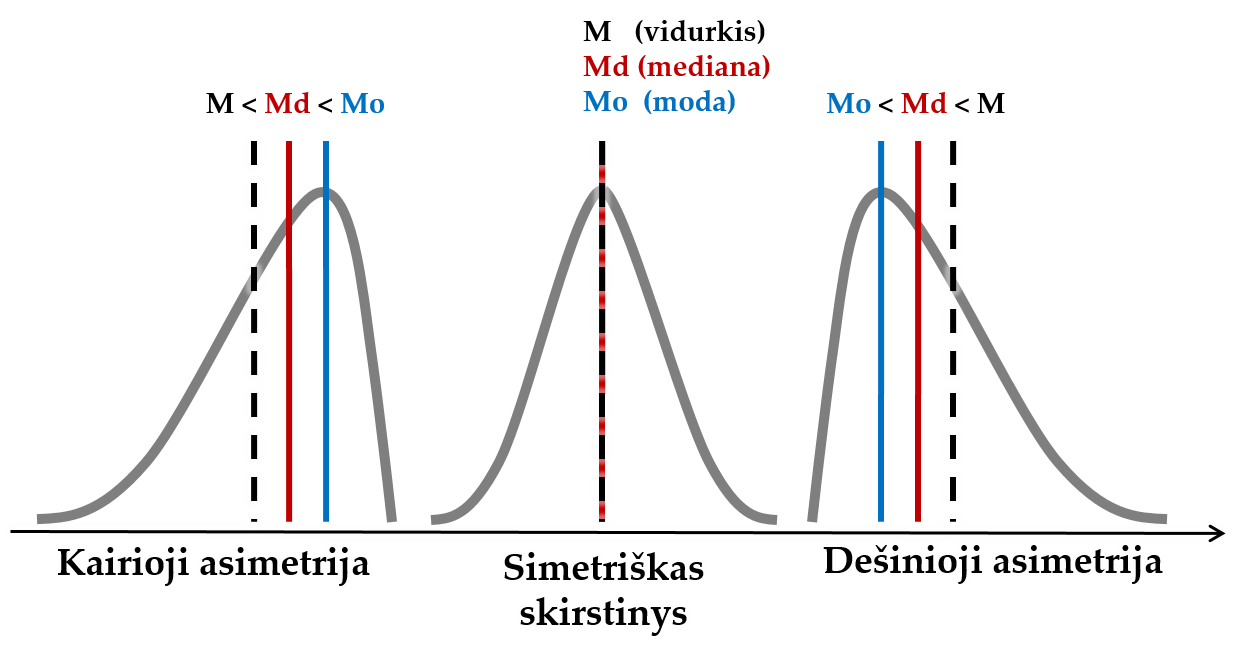
Apibendrinimas apie vidurkio, medianos ir modos tinkamumą pagal duomenų tipą pateiktas lentelėje 3.11.

¹ – tinka tik retais atvejais, jei vidurkis turi prasmę;
² – įprastai naudojama, kai mediana ir vidurkis smarkiai skiriasi;
³ – jei duomenys tolydieji, nykstamai maža tikimybė, kad gausime dvi vienodas reikšmes. Tad moda gali būti skaičiuojama nebent tik grupuotiesiems duomenims (intervalams) ir šiuo atveju priklauso nuo parinktų grupavimo parametrų.
3.8.2 Kaip statistiškai aprašyti vieno kintamojo reikšmes?
Prieš atliekant vieno kintamojo suvestines, reikia nustatyti kintamojo duomenų tipą. Panagrinėkime du kraštutinumus – nominaliuosius ir tolydžiuosius duomenis. Šiais atvejais – įprasti tokie pasirinkimai:
- Kategoriniams nominaliesiems duomenims pateikiama:
- imties dydis;
- dažnių lentelė.
- Tolydiesiems duomenims:
- imties dydis;
- duomenų centras (įprastai vidurkis arba mediana);
- duomenų sklaida (įprastai SD, kvartiliai Q1, Q3, IQR arba MAD).
Jei duomenys ranginiai arba skaitiniai diskretieji, jiems gali tikti ir tolydžiųjų, ir diskrečiųjų duomenų aprašymo metodai. Įvertinus, į ką – tolydžiuosius (t.y., kiekybinius) ar diskrečiuosius (t.y., nominaliuosius) duomenis – konkretus kintamasis panašesnis, parenkamas aprašomosios statistikos metodas. Įprasti pasirinkimai:
- Ranginiams duomenims:
- imties dydis*;
- dažnių lentelė*;
- mediana;
- kiti centrą (pvz., vidurkis) ir sklaidą (pvz., SD) aprašantys dydžiai naudojami tik tada, jei jie turi prasmę.
- Diskretiesiems skaitiniams duomenims:
- imties dydis;
- duomenų centras;
- duomenų sklaida;
- dažnių lentelė (įprasta tik tada, kai skirtingų reikšmių yra mažai).
* – privaloma.
3.8.3 Kaip pasirinkti kiekybiniams duomenims tinkamas suvestines?
Kai jau nustatėme, kad duomenys yra kiekybiniai (pvz., tolydieji), toliau žiūrime į duomenų pasiskirstymo formą ir įvertiname, ar yra išskirčių. Tokiu būdu nustatome, kokios statistikos geriausiai apibūdina duomenų centrą ir sklaidą (išsidėstymą apie tą centrą):
- Jei duomenys simetriški ir be ryškių išskirčių, įprastai centrui apibūdinti naudojamas aritmetinis vidurkis ir sklaidai – standartinis nuokrypis (SD).
- Jei duomenys smarkiai asimetriški arba turi ryškių išskirčių, labiau tinka išskirtims ir nukrypimams atsparios (robastiškos) statistikos: centrui – mediana, sklaidai – kvartiliai, MAD (medianinis absoliutusis nuokrypis nuo medianos), IQR (tarpkvartilinis plotis).
Galutinėje ataskaitoje tyrėjo nuožiūra pasirenkamas vienas labiausiai tinkantis centro padėties ir vienas sklaidos aprašymo būdas. Taip pat nurodomas ir imties dydis.
Statistiškai aprašant tolydžiuosius (kiekybinius) duomenis įprasta apibūdinti imties dydį, duomenų centro padėtį ir sklaidą.
3.9 Įprastinės ir išskirtinės reikšmės
Iki šiol nagrinėjome rodiklius, kurie apibūdina duomenų grupės charakteristikas. Dabar panagrinėsime temas, susijusias su atskirų duomenų taškų savybėmis.
3.9.1 Išskirtys
Reikšmes galime suskirstyti į 2 grupes: įprastinės ir išskirtinės. Išskirtines reikšmes dar vadiname išskirtimis (angl. outliers). Apibūdinimai:
- Išskirtys – išsiskiriančios, „kitokios“ reikšmės, nutolusios nuo pagrindinės duomenų „masės“.
- Išskirtys – tai imties reikšmės, nesiderinančios su pasirinktu statistiniu modeliu.
- Tai reikšmės, kurioms reikia skirti daugiau dėmesio.
3.9.2 Z reikšmės
Z reikšmė (angl. z score) – tai bedimensis tolydusis skaičius, parodantis, kiek standartinių nuokrypių reikšmė yra nutolusi nuo vidurkio. Z reikšmių yra tiek, kiek yra duomenų reikšmių: kiekviena reikšmė turi po ją atitinkančią z reikšmę. Z reikšmės gali būti tiek teigiamos (jei nuokrypis į didesnių), tiek neigiamos (jei nuokrypis į mažesnių reikšmių pusę). Pvz., z_i = -1{,}42 rodo, kad reikšmė x_i nuo vidurkio yra nutolusi per 1,42 standartinio nuokrypio.
Z reikšmė gaunama iš pradinės duomenų reikšmės atėmus vidurkį ir padalinus iš standartinio nuokrypio (lygtis 3.21). Tai z transformacija, dar vadinama standartizavimu. z_i = \frac{x_i - \overline{x}}{s_x} \tag{3.21}
Iš to išplaukia, kad z reikšmių vidurkis lygus 0, o standartinis nuokrypis (ir dispersija) yra 1. Visgi atkreipkite dėmesį, kad reikšmės nepakeičia skirstinio formos: jei skirstinys buvo asimetriškas, tai toks ir lieka (pvz., pav. 3.17).
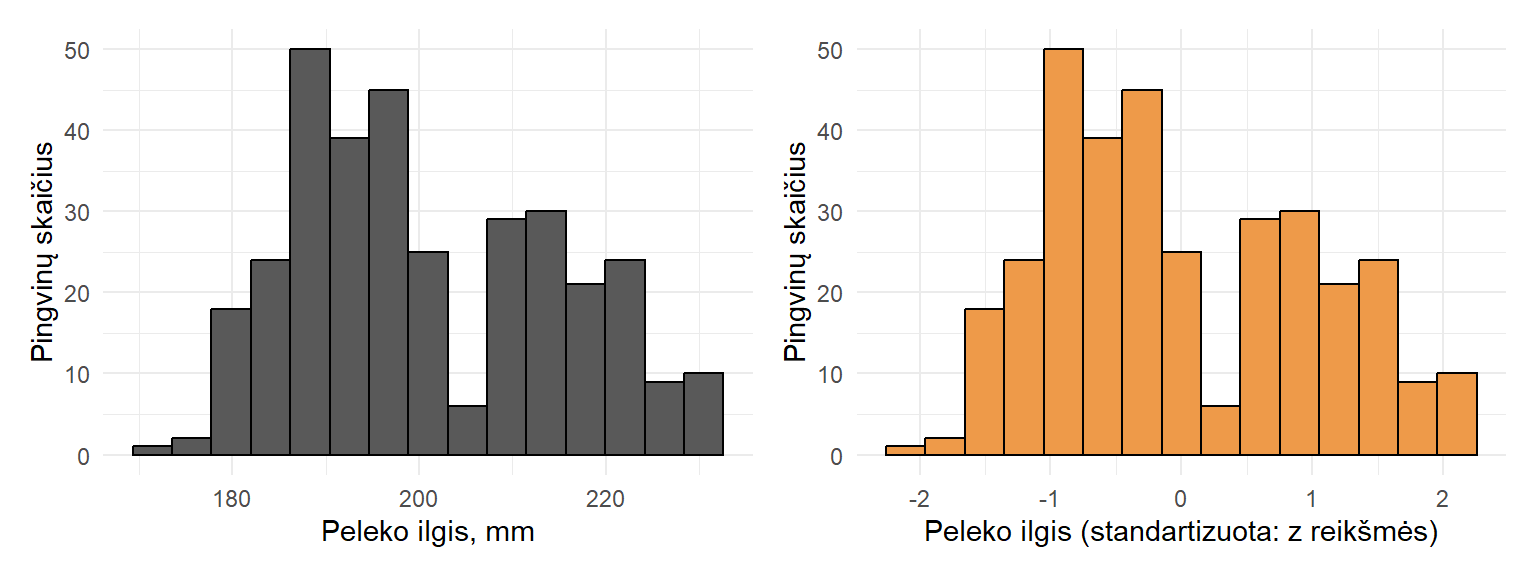
Z reikšmių naudojimo sritys:
- Z reikšmės parodo, kaip toli nuo vidurkio nutolusi konkreti reikšmė. Jos leidžia palyginti ne tik to paties, bet ir skirtingų kintamųjų reikšmių nutolimą nuo vidurkio (pvz., kas labiau nutolęs – to paties tiriamojo ūgis ar svoris).
- Jei duomenų skirstinys daugmaž normalusis, pagal z reikšmes galima vertinti, ar duomenų reikšmė įprastinė, ar išskirtinė:
- z \in (-2; +2) – įprastinės reikšmės;
- z \in (-3; -2] ~ \cup ~ [+2; +3) – sąlyginės išskirtys;
- z \in (-∞; -3] ~ \cup ~ [+3; +∞) – tikrosios išskirtys.
Papildoma (apie z reikšmes)
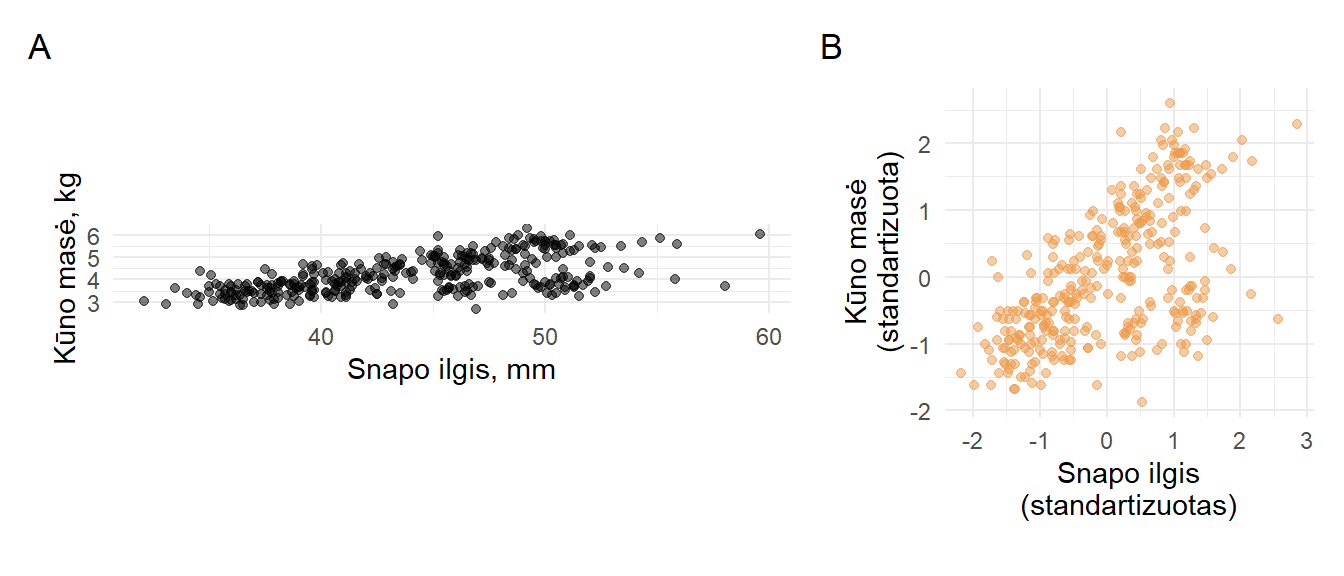
- Kadangi z reikšmės yra bedimensės (neturi matavimo vienetų) ir standartizuotos, pagal jas galima lyginti skirtingais vienetais matuojamus kintamuosius, juos atvaizduojant vienas šalia kito (pvz., pav. 3.18)
- Statistinio modeliavimo ir mašininio mokymosi srityje, kai turime daug aiškinamųjų kintamųjų, neretai vietoje įprastinių reikšmių naudojamos z reikšmės, nes:
- taip panaikinama skirtingų matavimo vienetų ir skirtingo sklaidos dydžio įtaka (pvz., pav. 3.19). Dėl to neretai galima gauti geresnius rezultatus ir įvertinti, kokio dydžio įtaką iš tiesų daro kiekvienas iš kintamųjų;
- Kai kurie algoritmai veikia geriau ir dėl to, kad kintamųjų vidurkis yra 0, o sklaida – vienoda.
Punktai 3 ir 4 šio kurso kontekste mažiau svarbūs.
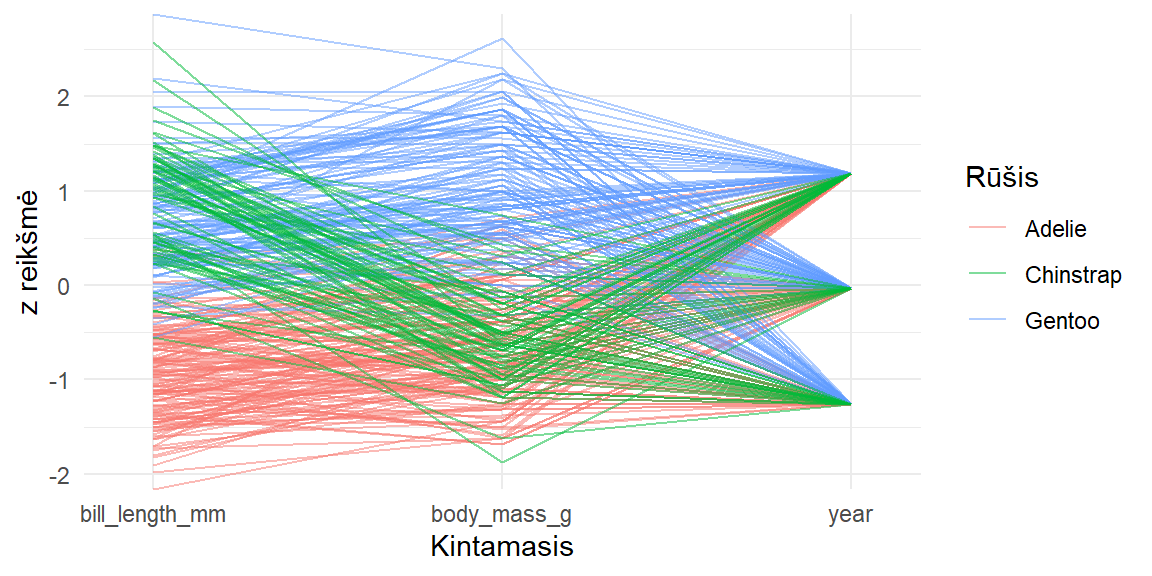
3.9.3 Barjerų metodas
Barjerų metodas – tai vienas iš būdų, skirtų atpažinti vienmačio pasiskirstymo11 išskirtis. Universalesnis nei z-reikšmių metodas, nes nereikia tenkinti normalumo sąlygos: pvz., tinka ir tada, jei skirstinys smarkiai asimetriškas. Jo esmė yra pagal kvartilių ir IQR reikšmes nustatyti taškus, vadinamus barjerais. Iš viso yra 4 barjerai: 2 vidiniai ir 2 išoriniai. Tarp vidinio ir išorinio barjero patekę taškai vadinami sąlyginėmis išskirtimis. Už išorinio barjero esantys taškai – tikrosiomis išskirtimis.
Barjerų apskaičiavimas:
- vidiniai barjerai: Q₁ – 1,5 × IQR ir Q₃ + 1,5 × IQR;
- išoriniai barjerai: Q₁ – 3 × IQR ir Q₃ + 3 × IQR.
Reikšmė, esanti ties vidinio barjero riba, dar nėra laikoma išskirtimi.
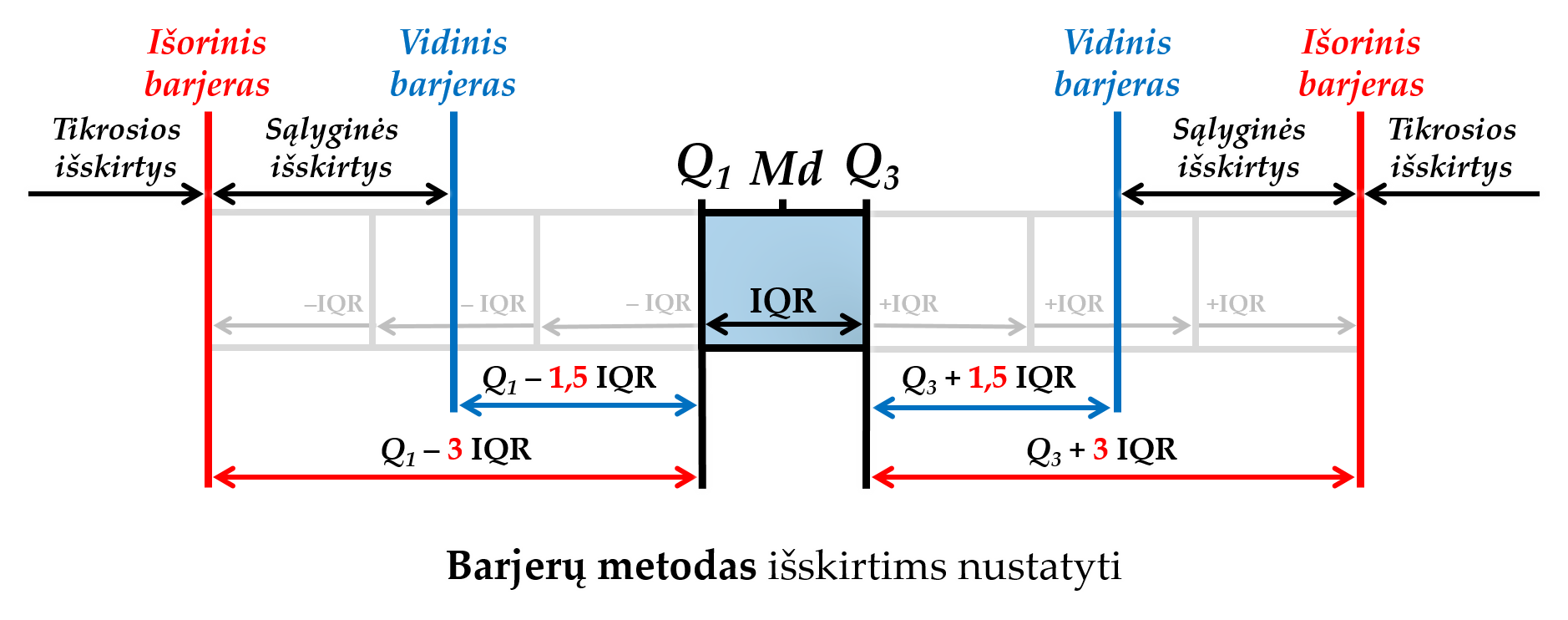
Kai kurie specialistai „sukauptuosius dažnius“ vadina „kaupiamaisiais dažniais.“↩︎
Angliškai į intervalus sugrupuotos reikšmės vadinamos terminu bins.↩︎
Vieni specialistai tą pačią savybę vadina „intervalo ilgiu“, kiti – „intervalo pločiu“.↩︎
„Duomenų centro padėtis“, „kintamojo reikšmių centro padėtis“, „centro padėtis“ arba tiesiog „duomenų centras“.↩︎
Jei kol kas nesuprantama, ką šiuo punktu norima pasakyti, tiesiog žinokite, kad tai yra naudinga ir bus svarbu darant statistines išvadas.↩︎
Vienodas skaičius reikšmių pašalinamas iš kiekvienos skirstinio pusės.↩︎
Šis MAD yra tai, kas angliškai vadinama median absolute deviation, o ne mean absolute deviation.↩︎
Atstumas taip pat gali būti vadinamas skirtumu ar nuokrypiu.↩︎
Kvartilių skirtumas (IQR) taip pat vadinamas tarpkvartiliniu pločiu, tarpkvartiliniu ilgiu, kvartilių užmoju↩︎
Smarkus nuokrypis nuo normaliojo pasiskirstymo.↩︎
„Vienmatis“ reiškia „pagal vieną kintamąjį“. „Daugiamatis“ reikštų, kad vienu metu atsižvelgiama į kelių kintamųjų reikšmes.↩︎
