2  Aprašomoji statistika: įvadas

Aprašomoji statistika – tai statistikos mokslo šaka, kurios esmė yra susisteminti (apibendrinti) imties duomenis ir glaustai perteikti esminius jų bruožus (nedarant išvadų apie generalinę aibę). Aprašomosios statistikos rezultatus vadinsime suvestinėmis.

Pav. 2.1. Aprašomoji statistika perteikia esminę informaciją apie imties duomenis.

Norėdami visapusiškesnės informacijos, skyrius apie aprašomąją statistiką galite rasti vadovėliuose (Čekanavičius ir Murauskas 2006, p.23–63; Venclovienė 2010; Field ir kt. 2012) bei J. McDonald knygos skyriuose (McDonald 2014a; McDonald 2014b).

2.1 Skaitiniai ir grafiniai metodai

Aprašomosios statistikos metodai yra skaitiniai ir grafiniai (pav. 2.2). Tad ir suvestinės yra dviejų rūšių:

  1. grafikai – juose greičiau pastebime tendencijas bei anomalijas;
  2. skaitiniai rezultatai (statistiniai rodikliai, koeficientai, lentelės) – suteikia tikslumo ir konkretumo.
Pav. 2.2. Aprašomosios statistikos metodai – skaitiniai ir grafiniai.

Grafikai ir skaitiniai metodai vieni kitus papildo. Tad įprasta duomenis pirmiausia tinkamai atvaizduoti, o po to grafikuose matomą informaciją patikslinti skaičiais. Visgi tam, kad suprastume grafikus, mokantis iš pradžių prasmingiau išmokti skaitinių metodų ir tik po to pereiti prie grafinių.

2.2 Kodėl reikalingos suvestinės?

Aprašomosios statistikos naudą aptarsime ir klausimą, kodėl reikalingos statistinės suvestinės, panagrinėsime analizuodami kačių tyrimo duomenis, pateiktus lentelėje 2.1. Žiūrėdami į šiuos duomenis, atsakykite į tokius klausimus:

  1. Kiek iš viso kačių ištirta?
  2. Kiek yra patelių ir kiek patinėlių? Ko daugiau? Kiek kartų (apytiksliai)?
  3. Kas šioje konkrečioje imtyje yra statistiškai1 didesni: patinėliai ar patelės?
  4. Kas pagal kūno svorį yra statistiškai2 panašesni vieni į kitus: patinėliai ar patelės?

Skirkite 1 minutę atsakymams rasti ir tik po to skaitykite tekstą po lentele.

Lentelė 2.1. Kačių tyrimo duomenys. Čia „sex“ – lytis (F – patelė, M – patinėlis), „body weight“ – kūno svoris (kg). Duomenų šaltinis – programos „R“ paketas „MASS“ (objektas cats).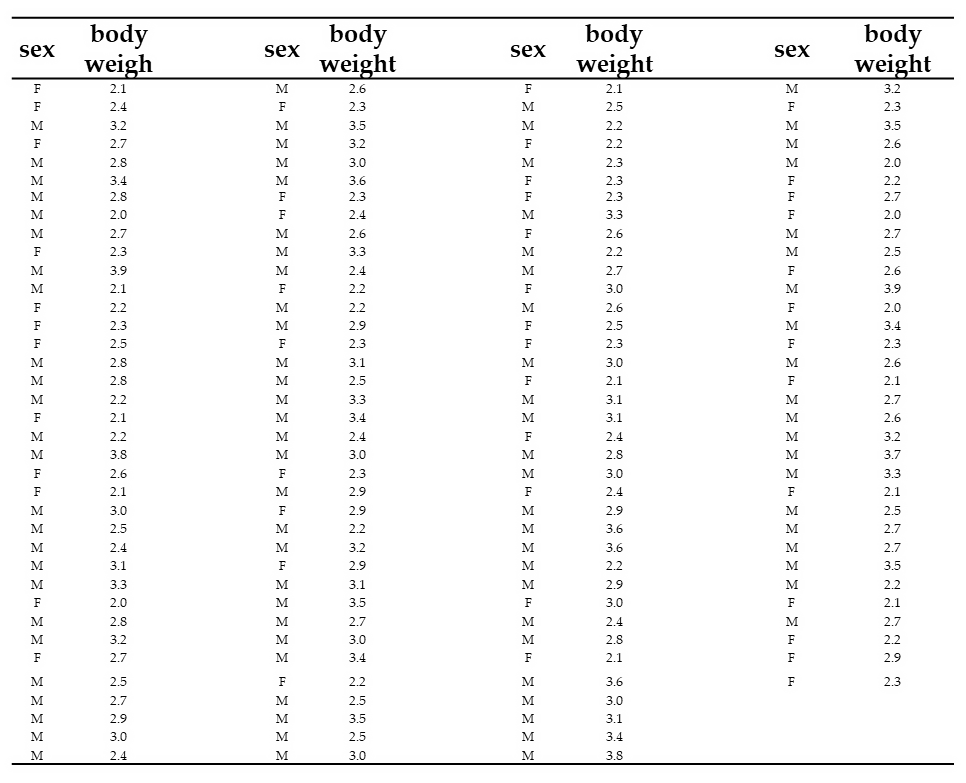

Žiūrint į pačius duomenis, tikėtina, atsakėte ne į visus klausimus. Ir naujų įžvalgų apie tiriamuosius taip pat padarėte nedaug. Tiesą sakant, galimai buvo problematiška netgi įžiūrėti tokiu mažu šriftu užrašytas reikšmes. O dabar pažiūrėkime į šių duomenų skaitines ir grafines suvestines, esančias suskleistoje sekcijoje „Suvestinės“ (pav. 2.3).

Suvestinės
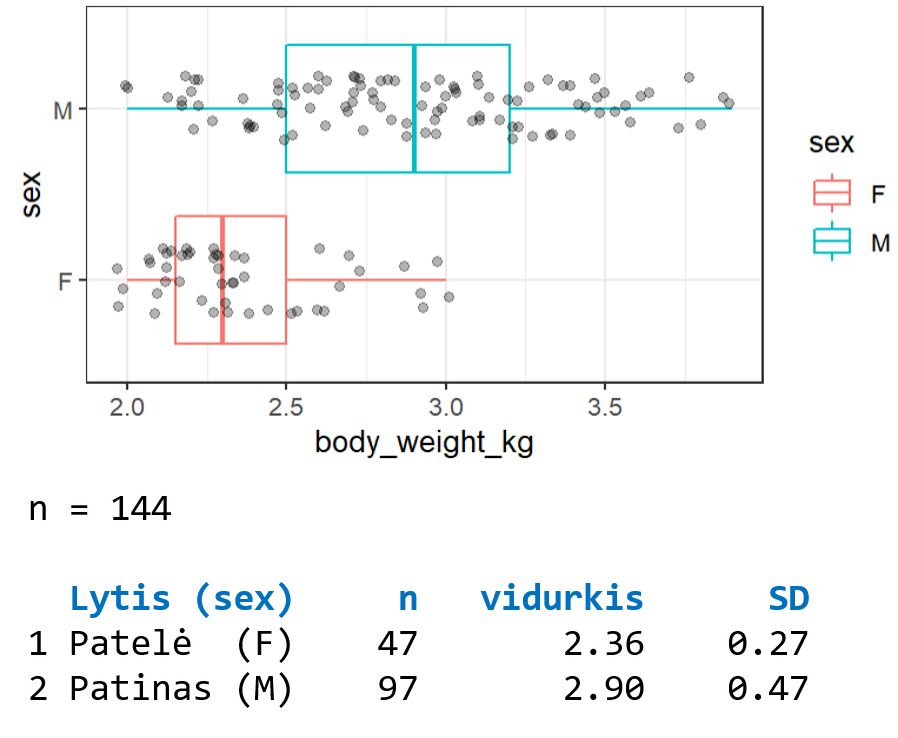
Pav. 2.3. Kačių tyrimo duomenų suvestinė: paveikslas ir lentelė. Čia „n“ – imties dydis, „SD“ – standartinis nuokrypis, „sex“ – lytis (F – patelė, M – patinėlis), „body_weight_kg“ – kūno svoris (kg).

Pagal pateiktą grafiką (nepaisant to, kad jis apipavidalintas tikrai ne idealiai) nesunku pastebėti tendencijas, koks preliminarus grupių dydis, kas yra statistiškai (šiuo atveju – vidutiniškai) didesni ir ar panašesni vieni į kitus. Skaitinės suvestinės lentelėje suteikia konkretumo papildydamos grafiką skaičiais: imties ir grupių dydžiu, vidurkio ir standartinio nuokrypio reikšmėmis. Turbūt nereikėjo nė minutės norint atsakyti į aukščiau pateiktus klausimus? Savo atsakymus palyginkite su pateiktais žemiau.

Atsakymai į klausimus
  1. Iš viso ištirtos 144 katės.
  2. Patinėlių beveik 2 kartus daugiau.
  3. Imties patinėliai yra vidutiniškai didesni nei patelės:
    • patinėlių duomenų taškų debesėlio centras pasislinkęs į didesnių reikšmių pusę, vidurkis didesnis;
  4. Imties patelės yra vidutiniškai panašesnės vienos į kitas nei patinėliai:
    • patelių duomenų taškai išsidėstę glaudžiau, standartinis nuokrypis mažesnis.

2.3 GA parametrai ir imties statistikos

Padiskutuokime apie skaitinius metodus. Jeigu atliekant skaičiavimus naudojama visa generalinė aibė (GA), tada rezultatą – apskaičiuotąją GA charakteristiką – vadiname generalinės aibės parametru (pvz., GA vidurkis). Jei analogiškiems skaičiavimams naudojami imties duomenys, tada rezultatą – imties charakteristiką – vadiname imties statistika (pvz., imties vidurkis).

Generalinė aibė → parametras.
Imtis → statistika.

Terminu „skaitinės suvestinės“ vadinsime aprašomąsias statistikas, tokias kaip imties dydis, vidurkis, standartinis nuokrypis, asimetrijos koeficientas, bei lenteles, tokias kaip dažnių lentelė.

Statistikomis vadinami dydžiai, apskaičiuoti iš imties duomenų (pvz., imties mediana).

2.4 Statistikų klasifikavimas

Imties statistikas galima skirstyti į kelias sąlygines grupes (pav. 2.4):

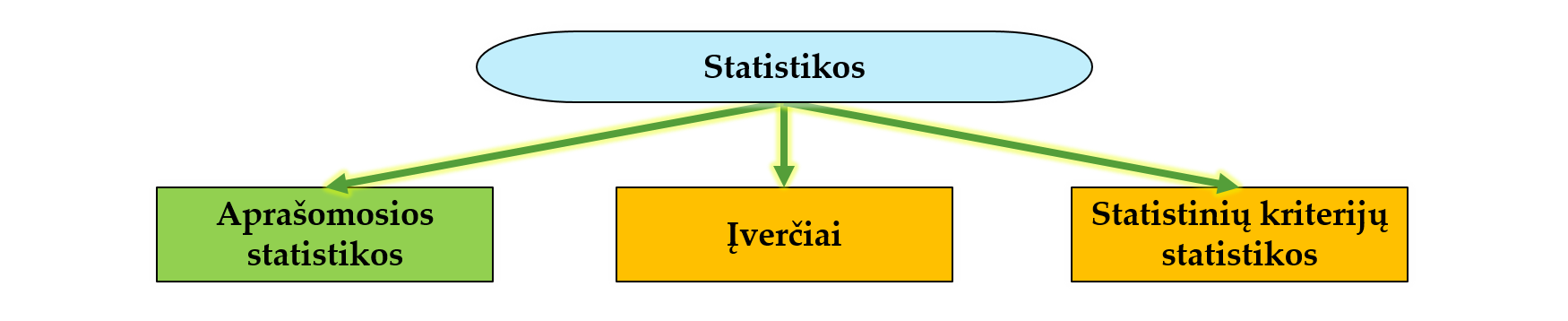
Pav. 2.4. Imties statistikų rūšys. Šiame skyriuje nagrinėsime aprašomąsias statistikas.
  1. Aprašomosios statistikos – charakteristikos, skirtos glaustai apibūdinti imties duomenis. Aprašomųjų statistikų pavyzdžių pateikta pav. 3.1.
  2. Įverčiai – tai, pagal turimus imties duomenis, geriausias spėjimas, koks yra tikrasis GA parametras (pvz., tikrasis vidurkis). Būna 2 rūšių:
    1. taškiniai įverčiai;
    2. intervaliniai įverčiai (pvz., pasikliautinieji intervalai).
  3. Statistinių kriterijų statistikos – tai dydžiai, kurių pagalba tikrinamos statistinės hipotezės ir daromos statistinės išvados (pvz., Stjudento3 kriterijaus t statistika).

2.5 Kompetencijos vykdant analizę

Šiame kurse susipažinsime su įvairiais koeficientais, rodikliais, grafikais, analizėmis ir kitokiais statistiniais metodais. Yra kelios pagrindinės su kiekvienu iš jų susijusios kompetencijos:

  1. Parinkti: tinkamai situacijai pasirinkti tinkamą metodą;
  2. Suprasti skaičiavimus: suprasti, kaip atliekami skaičiavimai, t.y., kokia skaičiavimų matematika ir logika (ir bent jau paprasčiausius uždavinius sugebėti patiems išspręsti „ranka“);
  3. Taikyti kompiuteriu: mokėti rodiklį apskaičiuoti, grafiką nubraižyti, o analizę atlikti konkrečia kompiuterine programa;
  4. Suprasti rezultatus ir mokėti juos teisingai interpretuoti.

Tad mokantis patarčiau nepalikti „aklų dėmių“ ir kiekvieną metodą išmokti visapusiškai. Ši knyga-konspektas skirta teorinei daliai, kompiuterinių skaičiavimų dalis neįtraukta.

  1. „Statistiškai“ reiškia, kad nagrinėjame vidutines visos grupės tendencijas, o ne atliekame, tarkime, 2 individų palyginimą.↩︎

  2. „Statistiškai“ reiškia, kad nagrinėjame vidutines visos grupės tendencijas, o ne atliekame, tarkime, 2 individų palyginimą.↩︎

  3. Stjudentas – mokslininko William Sealy Gosset slapyvardis.↩︎