1  Pradinės sąvokos ir principai

Jūsų užduotis studijuojant šį skyrių – susipažinti su bazinėmis šio kurso sąvokomis ir idėjomis.

1.1 Duomenys ir informacija

Turbūt esate girdėję pasakymą, kad duomenys yra „naujoji nafta“. Nafta yra išgaunama dideliais kiekiais, bet pradine (žaliavine) forma nėra itin naudinga. Žaliavinę naftą reikia perdirbti, o tada jau galima naudoti iš jos pagamintus produktus, tokius kaip suskystintos dujos, benzinas ar asfaltas, kurie ir yra tikrasis „lobis“. Panašiai yra ir su duomenimis.

Duomenys ≠ Informacija

Duomenys yra tam tikra forma pateikti faktai, kuriuos galima įrašyti, apdoroti, perduoti, saugoti ar ištrinti. Jie patys savaime vertės nekuria.

Informacija – tai žinios, tam tikrame kontekste turinčios prasmę. Jos padeda pastebėti tendencijas, bendrumus bei skirtumus tarp grupių ir geriau suprasti analizuojamą sistemą. Turėdami reikiamos informacijos galime imtis reikiamų veiksmų ir taip efektyviai sukurti naudą.

Duomenų analizė yra procesas, kurio metu iš duomenų išgaunamas „produktas“ – informacija.

\text{Duomenys} ~ {\xrightarrow{~\text{Analizė}~}} ~ \text{Informacija}

Diskusiją apie tai, kas yra duomenys, pratęsime poskyryje 1.8, kai žinosime daugiau apie statistiką ir duomenų analizę.

1.2 Statistika

Statistika (pranc. statistique, lot. status – būklė, padėtis) – tai mokslas, tiriantis kiekybinius masinių visuomeninių ir gamtos reiškinių aspektus kartu su tų reiškinių kokybiniu turiniu ir siekiantis atskleisti tų reiškinių visumos bendrąsias savybes (Vaitkevičiūtė 2001). Statistiką taip pat galima apibūdinti kaip tikslųjį mokslą apie duomenų rinkimą, sisteminimą, analizę ir gautų rezultatų interpretavimą (Bagdonavičius ir Kruopis 2015; Čekanavičius ir Murauskas 2006).

Pačią statistiką galima suskirstyti į matematinę bei taikomąją:

  • Pagrindinis matematinės statistikos dėmesys nukreiptas į matematikos ir tikimybių teorijos principus, statistikos teorijos ir metodų plėtrą bei tyrimus. Tai labiau teorinė, labiau abstrakti sritis, kuriai konkretūs tyrimo objektai ar konkrečios praktinio pritaikymo sritys mažiau svarbios.
  • Taikomoji statistika statistikos teoriją priartina prie tam tikros srities – žemės ūkio, inžinerijos, sporto, medicinos, kultūros, socialinių mokslų ar kitos – bei taiko statistikos principus šios srities problemoms spręsti (Martišius ir Kėdaitis 2013). Kai kurios taikomosios statistikos sritys netgi turi specifinius pavadinimus, pavyzdžiui:
    • psichologijos tyrimų metodologija ir statistika – psichometrija,
    • ekonomikos statistika – ekonometrija,
    • cheminių sistemų ir spektroskopinių signalų statistika – chemometrija,
    • biomokslų (medicinos, biologijos, genetikos ir kitų bio sričių) statistika – biostatistika.

Šiame kurse labiausiai koncentruosimės ties biostatistikai svarbiausiomis temomis. Visgi, daugelis principų bendri visoms statistikos sritims.

1.3 Generalinė aibė ir imtis

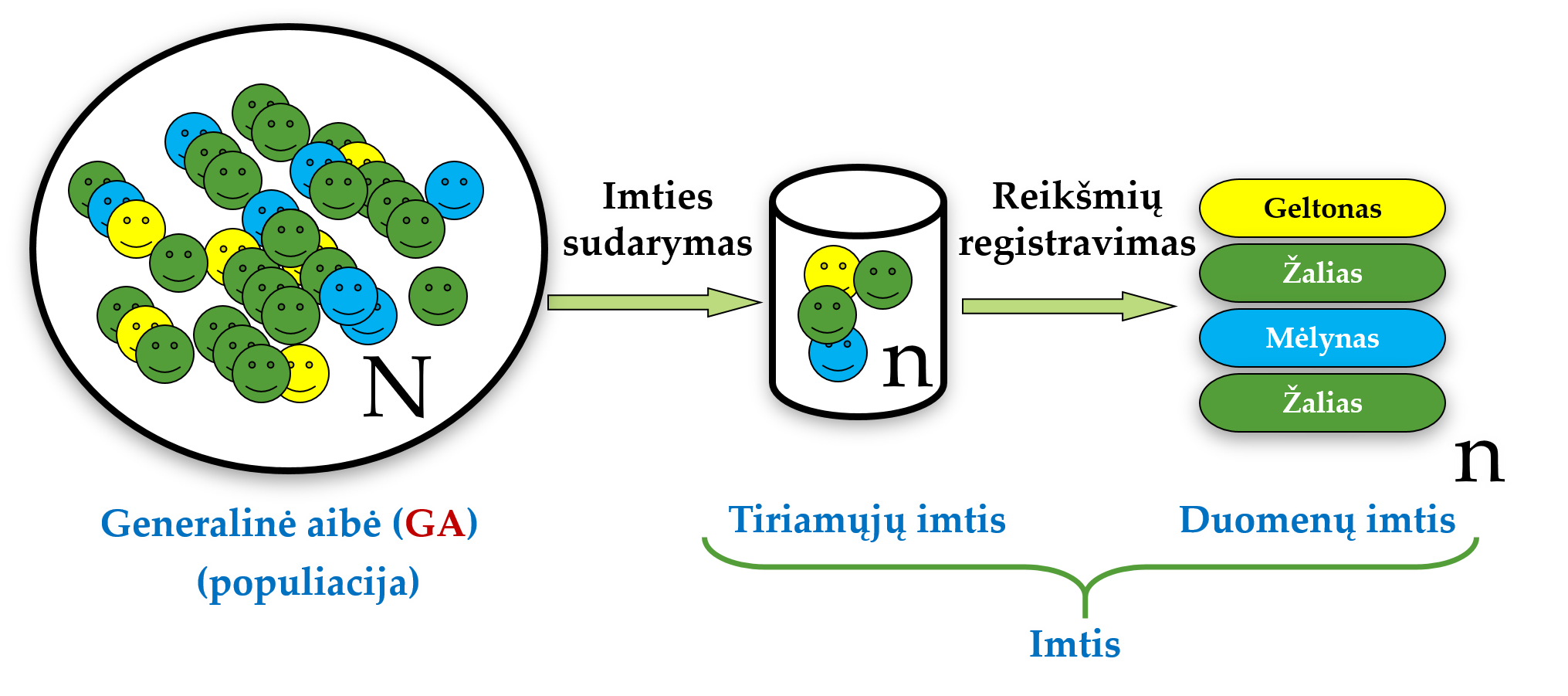
Statistika tiria masinius reiškinius – apibūdina tiriamųjų mases, t.y., aibes. Išskiriamos dvi aibių rūšys: generalinė aibė (populiacija) ir imtis (Pav. 1.1).

Pav. 1.1. Generalinė aibė, imtis ir duomenys. Iš visos tyrimo metu analizuojamos objektų visumos (generalinės aibės, GA) visiškai atsitiktinai arba kitu tikimybiniu būdu sudarome tiriamųjų imtį (paimame dalį GA). Tada išmatuojame ar užregistruojame vieną arba kelis mus dominančius tiriamųjų požymius ir taip gauname duomenis (duomenų imtį). Žymėjimai: N – generalinės aibės dydis, n – imties dydis.
Populiacija (statistikoje) ≠ biologinė ar geografinė populiacija

Generalinė aibė (GA), arba populiacija statistikos prasme, (angl. population) – tai statistinio tyrimo metu visa tyrėją dominanti objektų visuma. Pvz., visi diabetikai, visos chlorofilo molekulės. Dominančių objektų neretai yra žymiai daugiau, nei galima ištirti tyrimo metu. Tad įprastai tiriame ne visus mus dominančius objektus, bet tik jų dalį, vadinamą imtimi (angl. sample). Pvz., tik tuos diabetikus, apie kuriuos surinkome duomenis, tik tas chlorofilo molekules, kurias išskyrėme tyrimo metu. Ne visą GA tiriame ne tik todėl, kad resursai (laikas, pinigai, galimybės, skaičiuojamieji bei kitokie ištekliai) yra riboti, bet ir todėl, kad pakankamai tikslias išvadas galima padaryti ištyrus tik dalį GA.

Beje, šio kurso kontekste darydami statistines išvadas darysime prielaidą, kad GA yra be galo didelė (arba artima tokiai).

Generalinė aibė – visi dominantys objektai.

Imtis – į tyrimą patekusi GA dalis.

Imties dydis (angl. sample size, žymėsime n) – tai imties narių skaičius. Pvz., ištirtų diabetikų skaičius.

Pastabos:

  • Atkreipkite dėmesį į tai, kad terminas „populiacija“ statistikoje reiškia ne tą patį, ką biologijoje, ekologijoje ar demografijoje, todėl, vengiant dviprasmybės, lietuvių kalba yra aprobuotas kitas statistinis terminas („populiacijos“ sinonimas) – generalinė aibė (GA).
  • Terminas „imtis“ gali reikšti ir tiriamųjų imtį (pvz., į tyrimą įtraukti 4-5 m. amžiaus naminiai šunys), ir duomenų imtį (pvz., tyrimo metu užregistruota kiekvieno iš šių šunų kailio spalva; žr. Pav. 1.1). Tikiuosi, konkrečioje vietoje pagal kontekstą suprasite, apie ką kalbama, ir dėl dviprasmybės problemų nekils.

1.3.1 Statistiniam modeliavimui tinkama imtis

Statistiniam modeliavimui tinkama imtis, pagal kurią galima daryti patikimas statistines išvadas ar prognozes, turėtų būti reprezentatyvi. Tai svarbiausia imties savybė:

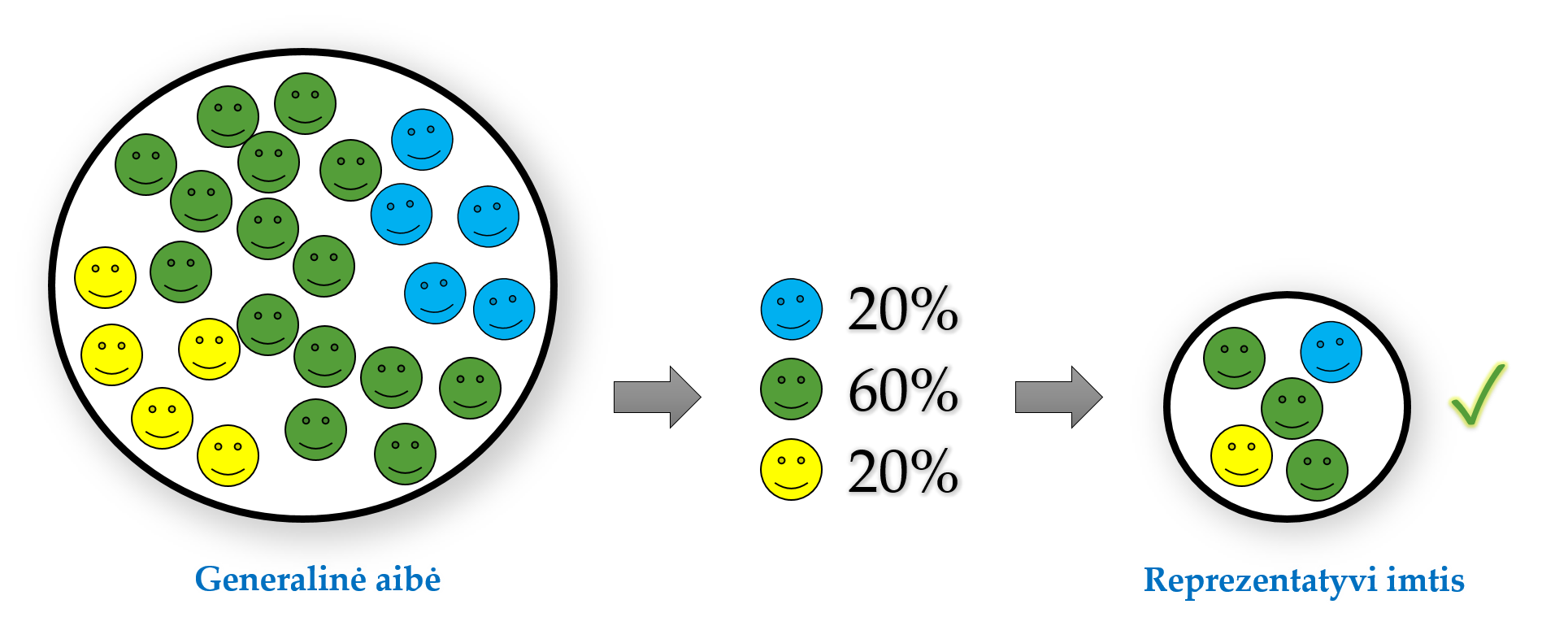
  • Reprezentatyvi imtis yra tokia, kurioje pakankamai tiksliai atsispindi vìsos GA savybės, svarbios tyrimui. Tad pagal reikšmių pasiskirstymą1 tokia imtis yra tarsi maža GA kopija. Tad iš tokios imties galima daryti patikimas išvadas.

    Imtis turi būti reprezentatyvi tai GA, apie kurią norime daryti išvadas, kitaip išvados bus klaidingos arba bent jau nekorektiškos. Pvz. jei turime galimybę ištirti tik savo 19-24 m. kolegas studentus vyrus, o išvadas norime daryti apie visus žmones Lietuvoje, tarp kurių yra ir vyrai, ir moterys, ir kūdikiai, ir vaikai, ir jaunimas, ir vyresnio (net pensijinio) amžiaus žmonės, tai ar tikrai iš turimos imties išvados apie nurodytąją GA bus korektiškos?

Reprezentatyvi imtis gerai atitinka GA savybes ir yra tarsi maža GA kopija.

Pav. 1.2. Reprezentatyvi imtis – pagal reikšmių proporcijas tarsi maža GA kopija.
  • Pakankamo dydžio imtis. Per mažo dydžio imtys yra nereprezentatyvios ir iš jų padarytos išvados, tikėtina, bus klaidingos. Pvz., jei generalinėje aibėje yra 5 galimos akių spalvos, o mes galime ištirti tik 3 tiriamuosius, tai įvertinti, kuri akių spalva pasitaiko dažniausiai, tokio kiekio tiriamųjų tikrai nepakanka. Realybėje pasakyti, kokio dydžio imtis yra maža ar per maža įprastai ganėtinai sunku, nes neturime visos reikiamos informacijos (o tyrimą vykdome būtent todėl, kad norime gauti daugiau reikiamos informacijos). Kai kurioms analizėms galima atlikti reikiamo minimalaus imties dydžio skaičiavimus. Bet ne visais atvejais tokie skaičiavimai įmanomi. Visgi neretai tikima, kad kuo imtis didesnė, tuo ir išvadų patikimumas didesnis. Deja, vien tik didelis imties dydis irgi pats savaime negarantuoja reprezentatyvumo, jei imtis sudaryta netinkamu būdu (pvz., jei yra netikimybinė).

Per mažos imtys yra nereprezentatyvios.

Didelis imties dydis irgi pats savaime negarantuoja reprezentatyvumo.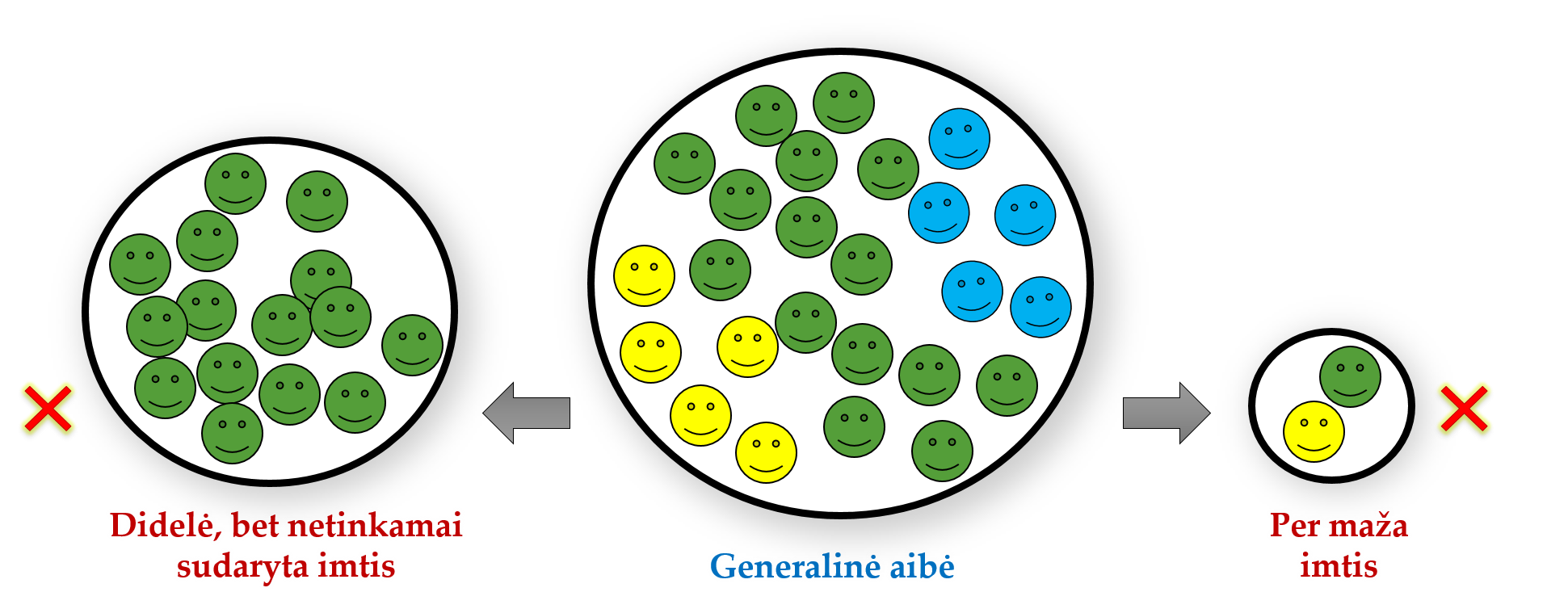
Pav. 1.3. Nereprezentatyvios būna tiek per mažos, nesugebančios tinkama proporcija atitikti GA savybių, tiek didelės, bet netinkamai sudarytos, imtys.
  • Tikimybinė imtis (angl. probability/probabilistic sample) yra sudaroma taip, kad kiekvienam objektui būtų žinoma (dažniausiai vienoda) tikimybė patekti į imtį. Tokiu atveju atsitiktinumas sudarant imtį yra griežtai apibrėžtas ir gali būti aprašytas matematiškai taikant tikimybių teorijos principus. Šiuo atveju atsitiktinumo įtaką galime įvertinti apskaičiuodami, pvz., neapibrėžtumo dydį2. Jei atsitiktinumas nėra griežtai apibrėžtas, tai jo įtakos įvertinti negalime, o išvadų pagrįstumas tampa abejotinas.

Tikimybiškai sudaryta imtis leidžia statistiškai įvertinti atsitiktinumo įtaką.

Imtis, kuri yra pakankamo dydžio (ne per maža) ir tikimybinė, įprastai yra ir reprezentatyvi. Visgi, net idealus imties sudarymo būdas negarantuoja 100% reprezentatyvumo, tad statistinės išvados (apie jas bus rašoma 1.4 poskyryje) daromos su tam tikra paklaida.

Imtis, kuri yra pakankamo dydžio ir tikimybinė, įprastai yra ir gana reprezentatyvi.

Pav. 1.4. Tikrųjų GA savybių nežinome (todėl ir atliekame tyrimą). Tad, tikėtina, kad net idealiai sudaryta imtis bus bent šiek tiek nereprezentatyvi. Tikrojo nereprezentatyvumo laipsnio nežinome. Visgi, jei imtis sudaryta tinkamai, teisingai parinkti analizės metodai gali į šį neapibrėžtumą atsižvelgti.

1.4 Statistikos šakos

Žinant, kokios yra aibės, toliau aptarkime statistinės analizės metodų grupes. Tradiciškai statistikos metodus galima suskirstyti į dvi pagrindines šakas:

  1. Aprašomoji statistika (angl. descriptive statistics). Jos tikslas – glaustai apibūdinti esmines surinktų duomenų savybes, nedarant išvadų apie generalinę aibę. Šiai šakai priklauso tiek skaitiniai, tiek grafiniai duomenų apibendrinimo metodai. Skaitinių metodų pavyzdžiai: vidurkių, medianų, standartinių nuokrypių bei kitokių koeficientų ar rodiklių skaičiavimas, dažnių lentelių sudarymas. Grafinių metodų pavyzdžiai: histograma, stulpelinė, stačiakampė ar sklaidos diagrama. Apie kiekvieną iš paminėtųjų metodų išsamiau mokysimės vėliau.
    • Skaitiniai metodai – kurių rezultatai įprastai išreiškiami skaičiais. Kartais terminą „skaitiniai“ vartosiu apibūdinti visus ne grafinius metodus.
    • Grafiniai metodai – kurių rezultatas yra grafikai bei diagramos.
    Aprašomoji statistika – glaustas surinktų duomenų savybių apibendrinimas – įprastai yra pirmasis analizės etapas. Pagal jo rezultatus galima pastebėti dėsningumus, tendencijas bei pasirinkti tolimesnės analizės (jei tokios reikia) eigą.

Aprašomosios statistikos esmė – glaustai apibūdinti esmines imties duomenų savybes.

  1. Statistinės išvados (angl. inferential statistics). Įprastai statistinio tyrimo metu duomenis surenkame iš dalies mus dominančių objektų – imties,– o išvadas siekiame daryti apie visus dominančius – generalinę aibę (GA). Pagal imties, kuri yra mažesnė už GA, duomenis padarytos išvados apie visą GA ir yra statistinės išvados. Dėl GA ir imties dydžio skirtumų atsiranda neapibrėžtumas (angl. uncertainty), kurį ir siekiama įvertinti (kuo mažesnis neapibrėžtumas, tuo didesnis tikslumas bei užtikrintumas). Statistinės išvados daromos (1) sudarant taškinius įverčius (angl. point estimates), (2) sudarant pasikliautinuosius intervalus (angl. confidence intervals) bei (3) tikrinant statistines hipotezes (angl. statistical hypothesis testing). Šioje srityje dažnai girdimos sąvokos yra p reikšmė bei statistinis reikšmingumas. Statistinių išvadų darymas yra grindžiamas tikimybių teorijos dėsniais ir aksiomomis. Tad tam, kad būtų įmanoma korektiškai įvertinti neapibrėžtumą ir išvados būtų korektiškos, imtis turi būti sudaryta tinkamai. Tai pasiekiama tik gerai suplanavus ir tinkamai įvykdžius tyrimą. Atkreipkite dėmesį, kad net ir idealiai suplanavus ir atlikus tyrimą, statistiniais metodais išvadas darome ne 100% tikslumu, todėl yra galimybė apsirikti.

Statistinės išvados – pagal imties duomenis padarytos išvados apie visą GA.

Pav. 1.5. Sąsaja tarp imties sudarymo, aprašomosios statistikos bei statistinių išvadų darymo. Atkreipkite dėmesį, kad kairėje ir dešinėje yra ta pati GA, skiriasi tik mūsų žinių lygis apie ją.

Pav. 1.5 („centrinė statistikos dogma“ ) vaizduoja, kaip susiję imties sudarymas, aprašomoji statistika ir statistinių išvadų darymas:

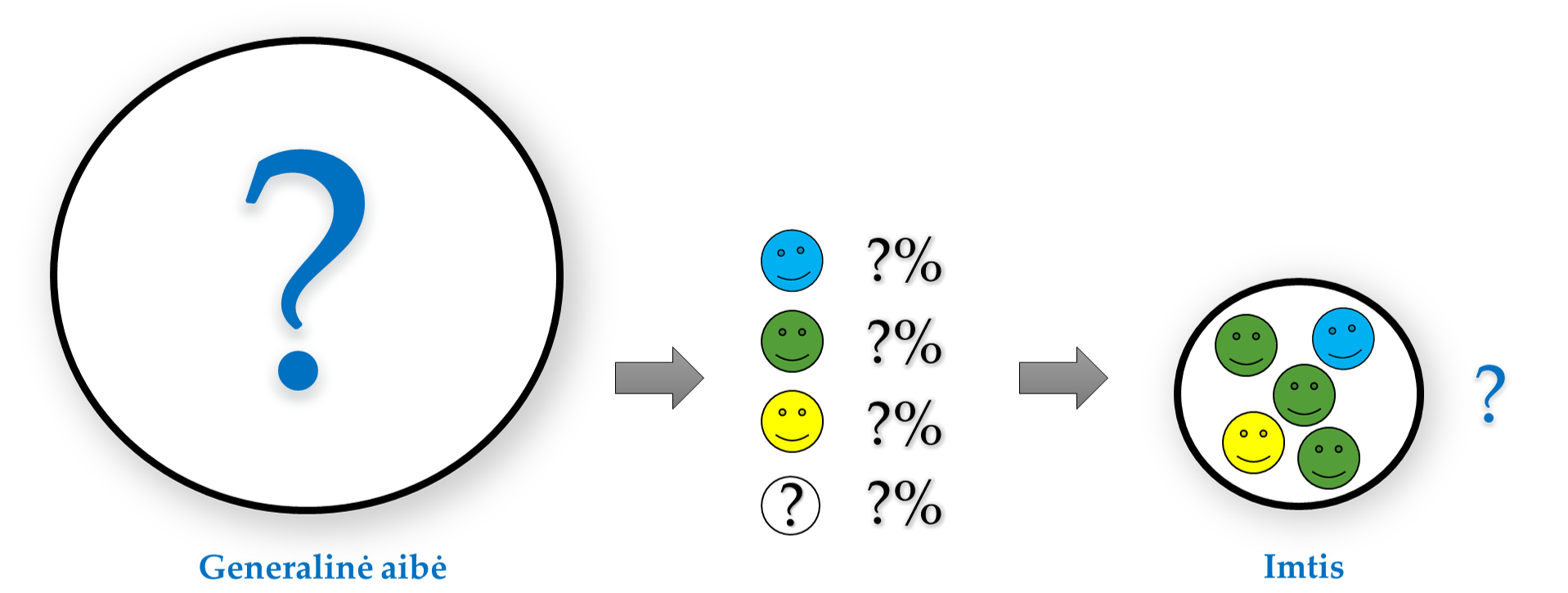
  1. iš GA, kurią norime tirti ir apie kurią neturime bent dalies informacijos (todėl objektai nenuspalvinti), pagal tikimybių teorijos principus sudarome imtį. Taip padidiname tikimybę, kad imtis bus reprezentatyvi (žr. sk. 1.3.1).
  2. aprašomosios statistikos metodais nustatome, kokie yra tiriamieji, kurie pateko į imtį. Apie visus likusius (t.y., apie GA) šie metodai informacijos nesuteikia.
  3. pasirenkame reikiamą statistinį modelį, kuris padeda įvertinti neapibrėžtumą, atsirandantį sudarant imtį. Tokiu būdu su tam tikra paklaida galime padaryti išvadas apie visą generalinę aibę. T.y., su tam tikra paklaida įvertinti GA savybes (todėl šioje dalyje objektai nuspalvinti).

Kiekviena iš statistikos šakų bei paminėti terminai plačiau bus nagrinėjami atskiruose skyriuose.

1.5 Žvalgomoji ir patvirtinančioji analizė

Pagal tai, kokia analizės paskirtis, duomenų analizės metodus galima suskirstyti į tokias grupes: žvalgomoji ir patvirtinančioji analizė.

  1. Žvalgomoji analizė (angl. exploratory data analysis, EDA3) – jos tikslas yra susipažinti su duomenimis, pastebėti ryšius, tendencijas, tiesiogiai nestebimas (latentines, vidines) duomenų struktūras (t.y., išžvalgyti duomenis) bei kelti naujas idėjas, hipotezes. EDA sudaro tiek aprašomosios statistikos, tiek ir sudėtingesni metodai, tokie kaip klasterinė analizė (kurios tikslas – atrasti panašių objektų grupes) ar daugiamačių duomenų atvaizdavimui skirti metodai, pvz., pagrindinių komponenčių analizė (PCA), uMap, daugiamačių skalių (MDS) metodai (PCoA, NMDS). Daug dėmesio skiriama grafiniam atvaizdavimui ir įvairaus tipo duomenų vizualizacijoms. Šiais metodais norima glaustai apibendrinti duomenis, rasti naudingų įžvalgų ar įdomių klausimų, kurie galėtų būti nagrinėjami toliau.

    Visgi EDA metodai gali parodyti tik tai, kaip yra konkrečiuose duomenyse, kuriuos tiriate. Patys savaime metodai neskirti apibendrinti, kaip yra visoje generalinėje aibėje. T.y., surinkus kitus duomenis rezultatai nebūtinai rodys tuos pačius dalykus. Taip yra todėl, kad atliekant EDA nėra griežtų taisyklių, kaip įvertinti paklaidas, todėl rezultatai yra tik preliminarūs. Iškeltas idėjas ir hipotezes reikia tikrinti matematiškai griežtesniais būdais.

    Pastaba. Jei hipotezes jau esame išsikėlę prieš analizę, tada EDA paskirtis yra tiesiog susipažinti su duomenimis prieš pereinant prie kito etapo.

Žvalgomoji analizė (EDA): susipažinti su duomenimis ir kelti naujas hipotezes.

  1. Patvirtinančioji analizė (angl.confirmatory data analysis, CDA) – jos tikslas yra patikrinti iš anksto suformuluotas hipotezes apie duomenis. Tai matematiškai griežtos statistinės procedūros, naudojamos siekiant nustatyti, ar duomenys neprieštarauja turimoms hipotezėms. Viena iš jų – statistinių hipotezių tikrinimas.

    Korektiškai atliekant statistinių hipotezių tikrinimą, hipotezės turi būti iškeltos prieš tai, kai pamatome duomenis, pagal kuriuos jos bus tikrinamos. Iš to išplaukia, kad naujų idėjų kėlimas turėtų būti vykdomas su vienais duomenimis (pvz., bandomojo, „pilotinio“ tyrimo metu, apžvelgiant kitų tyrimų rezultatus ar pan.), o iškeltų hipotezių tikrinimas – jau su kitais (pvz., naujai surinktais ar žvalgomosios analizės metu nenaudotais) duomenimis.

Patvirtinančioji analizė: patikrinti iš anksto suformuluotas hipotezes.

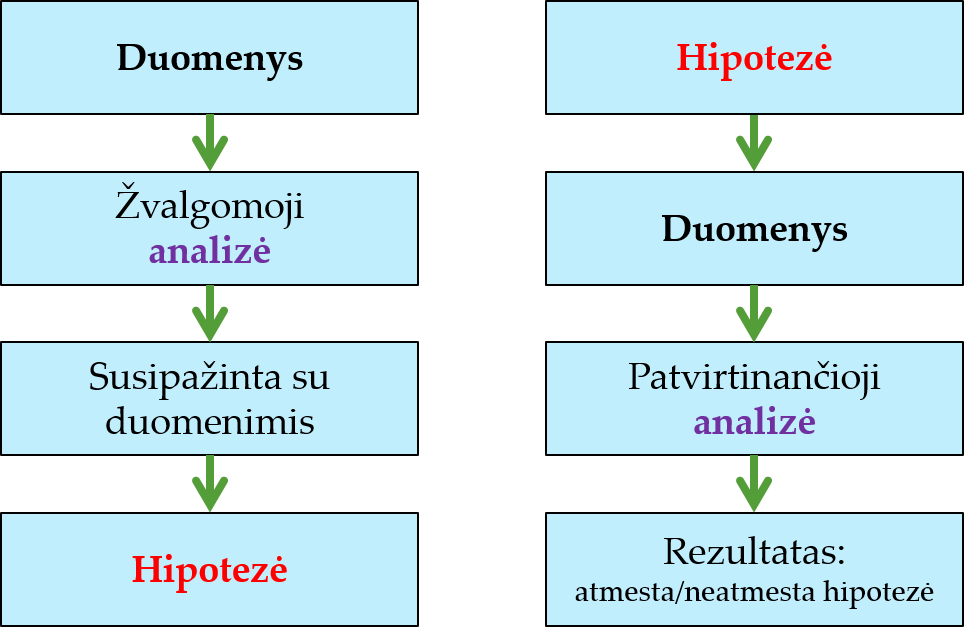
Pav. 1.6. Eiga vykdant žvalgomąją (EDA) ir patvirtinančiąją (CDA) analizes. EDA naudoja duomenis, kad susipažintume su duomenimis, gautume naujų įžvalgų ir idėjų: hipotezė čia yra rezultatas. O norint patikrinti jau turimą hipotezę, tuo tikslu suplanuojamas tyrimas, renkami duomenys, vykdoma CDA: hipotezė čia yra pradinis taškas.

Pavyzdys: po žvalgomosios analizės suformuluota hipotezė, kad didėjant pacientų amžiui mažėja tikimybė patirti tam tikrą medicininę būklę. Toliau surinkus naują duomenų imtį atlikta patvirtinančioji analizė: naudotas statistinių hipotezių tikrinimas siekiant išsiaiškinti, ar šis ryšys yra statistiškai reikšmingas (jei statistiškai reikšmingas, tada rezultatą galima apibendrinti ne tik imčiai, bet ir visai GA).

1.6 Statistinių tyrimų planavimas

Analizuodami Pav. 1.5 pastebėjote, kad be pagrindinių statistikos šakų, pažymėtų numeriais 2 ir 3, yra dar viena dalis, kuri turi būti atlikta prieš analizę. Ji susijusi su tyrimų planavimu ir vykdymu.

Statistinis tyrimas – tai tyrimas (angl. study, research), kurio metu yra renkami ir analizuojami statistiniai duomenys. Statistinių tyrimų planavimas yra tarpdisciplininė sritis, apimanti tiek statistikos, tiek kitų mokslinių metodologijų elementus. Statistika yra esminė jo dalis, nes ji suteikia įrankius ir metodus, padedančius užtikrinti, kad tyrimas būtų tinkamai suprojektuotas, duomenys būtų tinkamai surinkti ir analizė būtų patikima.

Pabrėžiu, kad norint tinkamai suplanuoti statistinį tyrimą, reikia tiek statistikos, tiek tiriamosios srities (pvz., biologijos, psichologijos, ekonomikos ar genetikos) žinių. Specialybinės tiriamosios srities žinios nėra statistikos mokslo objektas, tad norint iš tiesų gerai parengti tyrimo planą reikalingi ir tos srities žinių turintys, ir statistiką išmanantys ekspertai.

1.6.1 Įprastinė statistinio tyrimo eiga

Norint korektiškai atlikti analizę ir gauti patikimus rezultatus svarbu tiek tyrimą tinkamai suplanuoti, tiek ir tinkamai jį įvykdyti. Tai ypač svarbu siekiant daryti statistines išvadas, tikrinant statistines hipotezes, kas yra viena iš patvirtinančiosios analizės formų (žr. sk. 1.5).

Siekiant korektiškų ir patikimų rezultatų, tyrimas privalo būti tinkamai suplanuotas.

Pav. 1.7. Vienas iš būdingos statistinio tyrimo eigos variantų.

Planuojant tyrimą suformuluojama tiriamoji problema (tiriamasis klausimas), apibrėžiama, kas tiksliai yra generalinė aibė, apie kurią norima daryti išvadas, nusprendžiama, kaip bus sudaroma tinkama tiriamųjų imtis (žr. sk. 1.3.1), kurios tiksliai tiriamųjų savybės bus tiriamos ir kaip bus renkami duomenys, numatoma, koks tikslumo lygis yra pageidautinas, kokios analizės metodų grupės yra tinkamos atsakyti į suformuluotą klausimą (konkretūs metodai bus pasirinkti vėliau atlikus aprašomąją statistiką). Taip pat gali būti vertinga preliminariai numatyti, kur ir kaip bus skelbiami rezultatai ir išvados. Nuo to priklauso reikiamas tiriamųjų skaičius (imties dydis) bei kitos subtilybės. Jei tyrimas prastai suplanuotas ar duomenų surinkimo stadija netinkamai įvykdyta, mažai tikėtina, kad duomenų analizė pajėgs kompensuoti šiuos trūkumus. Pvz., surinkus ne tuos duomenis, kurių reikia, analizė tikrai bus bejėgė siekiant užsibrėžtų tikslų. Tad norint korektiškų rezultatų, planavimui privalo būti skiriamas prideramas dėmesys.

Duomenų analizė nekompensuos prastai suplanuoto ar netinkamai įvykdyto tyrimo klaidų.

1.6.2 Imties dydžio planavimas

Siekiant preliminariai sužinoti reikiamą minimalų imties dydį, kurio pakaktų su tam tikru patikimumu pasiekti statistiškai reikšmingą rezultatą (supaprastintai sakant, rezultatą, kuris, tikėtina, imtyje atsirado ne dėl atsitiktinumo), gali būti atlikta taip vadinama (statistinės) galios analizė (angl. power analysis). Ji galima kai kuriems modeliams/metodams, kai turime preliminarios informacijos apie GA.

1.7 Tiriamieji

Poskyryje 1.3 aptarėme aibes, kurias tiria statistika. Šios yra sudarytos iš elementų, apie kuriuos renkami duomenys. Tie elementai gali būti:

  • konkretūs objektai (pvz., svogūno ląstelės, pacientai, mėgintuvėliai);
  • reiškiniai, procesai ar kitokie abstraktesni dalykai (pvz., oro sąlygos, eismo įvykiai).

Taip pat gali būti:

  • pavieniai (pvz., atskiros raumenų ląstelės, pavienės bakterijos, mokiniai);
  • jų grupės (pvz., biologinės populiacijos, bakterijų kolonijos, mokinių klasės).

Priklausomai nuo tyrimo plano, tie patys elementai gali būti ištirti tik vieną kartą ar net kelis kartus, pvz., jei tyrimas atliekamas skirtingomis sąlygomis (tiriamasis, vartojantis vaistą, ir galimai tas pats tiriamasis, nevartojantis vaisto). Galimybių daug, todėl elementui, apie kurį renkama statistinė informacija, apibūdinti yra vartojamas bendresnis terminas – statistinis vienetas (angl. statistical unit). Stebėjimo vienetas, eksperimentinis vienetas ar tiriamasis vienetas – tai terminai, kurie vartojami kaip sinonimai.

Statistinis vienetas (angl. statistical unit) – tai atskiras elementas (tiriamasis, objektas, procesas, reiškinys) ar jų grupė tam tikru laiko momentu, periodu ar tam tikromis sąlygomis, apie kurį renkama statistinė informacija.

Stebėjimu (arba įrašu)4 vadiname visus duomenis, gautus iš vieno statistinio vieneto. Pastaba: terminas „stebėjimas“ savaime nereiškia, kad duomenys gauti žiūrėjimo metodu: jie gali būti užregistruoti, išmatuoti, išgirsti, pajausti, …

Statistinis vienetas (SV) yra tai, apie ką renkama informacija.

Stebėjimas yra visa apie SV surinkta informacija.

Toliau šiame skyriuje paprastumo dėlei darysime prielaidą, kad vienas tiriamasis ištirtas 1 kartą, todėl terminas „statistinis vienetas“ atitiks terminą „tiriamasis“.

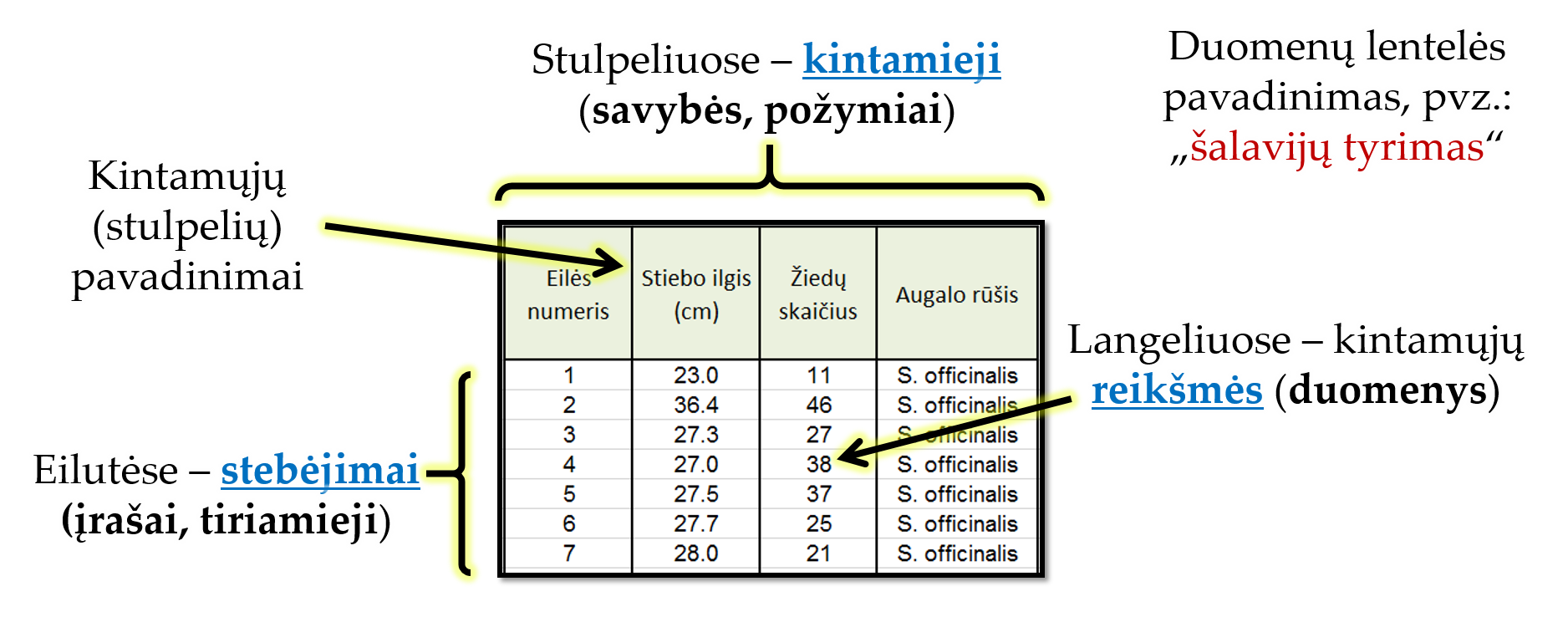
1.8 Kintamieji ir duomenys

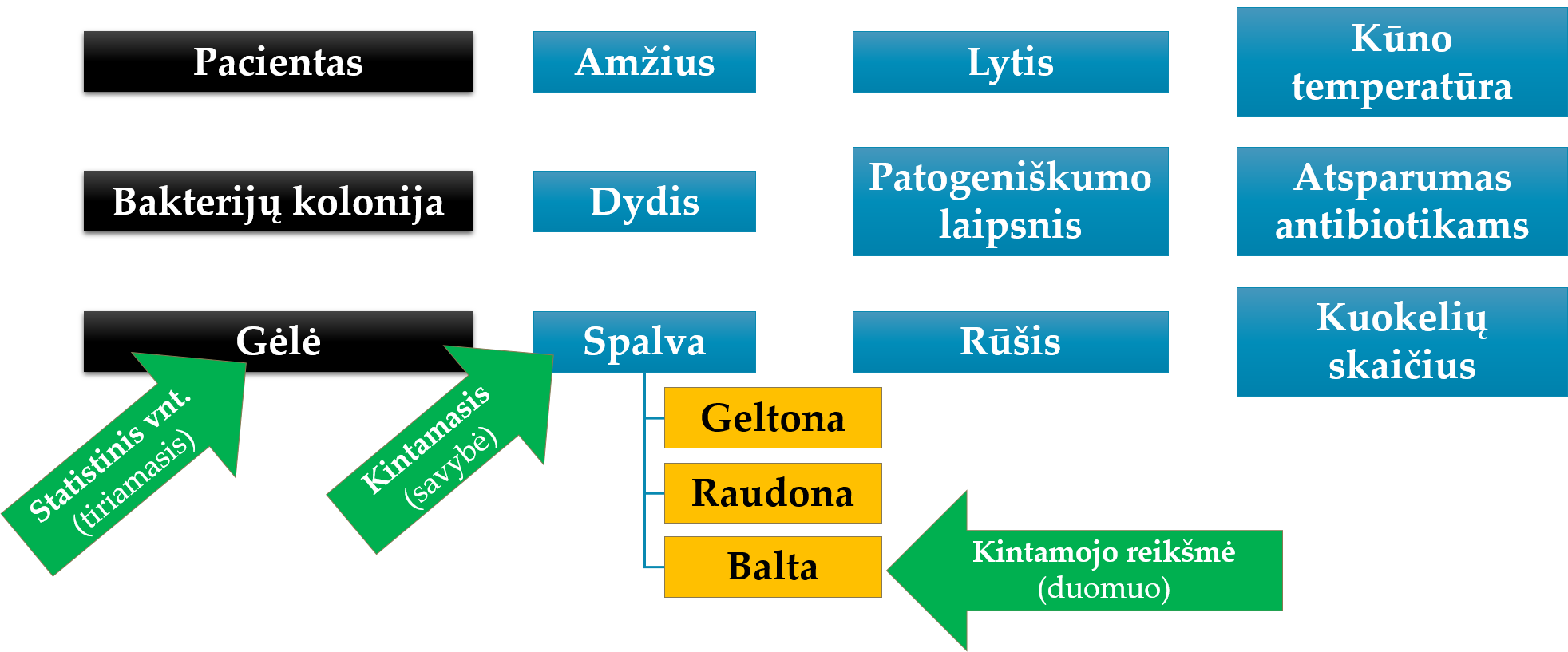
Tiriamieji turi vieną ar keletą tyrėją dominančių požymių. Kintamasis (angl. variable) yra tiriamųjų savybė, kuri skirtingiems tiriamiesiems gali įgyti skirtingas reikšmes. Pvz., amžius, lytis, ūgis, lankomas universitetas, naktį išmiegotų valandų skaičius, eritrocitų nusėdimo greitis ir pan. Taip pat atkreipkite dėmesį, kad kintamasis – tai vieno duomenų tipo seka.

„Kintamasis“ yra bendriausias įprastai statistikoje vartojamas terminas. Priklausomai nuo konteksto, savybės tipo bei taikymo srities galimi sinonimai: kintamasis, požymis, savybė, faktorius, rodiklis, indeksas, dydis, rodmuo, žymuo, …

Kintamasis yra viena tiriamųjų savybė.

Duomuo (angl. datum) – tai užregistruotas faktas apie tiriamąjį: konkreti kintamojo reikšmė konkrečiam tiriamajam.

Statistiniai duomenys (angl. data) šio kurso kontekste yra kokybinių ir kiekybinių kintamųjų reikšmės, priklausančios tiriamųjų aibei.

Duomenys – tai kintamųjų reikšmės.

Pav. 1.8. Ryšys tarp statistinių vienetų, kintamųjų ir duomenų.

1.9 Duomenų struktūros statistikoje

Statistinio tyrimo metu svarbu nuspręsti, kokia forma rinksime ir saugosime duomenis. Mūsų pasirinkimas priklauso nuo tyrimo srities, sprendžiamo uždavinio ir duomenų rinkinio sudėtingumo. Šio kurso metu dirbsime su struktūruotaisiais duomenimis ir dviem jų formomis (duomenų struktūromis) – duomenų sekomis ir duomenų lentelėmis. Tad siūlau skirti pakankamai laiko, kad tinkamai perprastumėte šias dvi struktūras.

1.9.1 Duomenų seka

Duomenų seka – tai duomenų reikšmės, surašytos tam tikra eilės tvarka. Sprendžiant uždavinius ant popieriaus šios sekos įprastai parašomos į eilutės pavidalą, tad dažnai statistikoje dar vadinama duomenų eilutėmis. Visgi „duomenų seka“ yra bendresnis terminas. Duomenų sekos pavyzdys – išmatuoti kurso kolegų ūgiai (centimetrais): 180, 168, 171, 173, 185, 179, 164.

Vienoje sekoje įrašomos vienõs užregistruotos tiriamųjų savybės (tarkime, apklaustųjų ūgio) reikšmės. Tad duomenų seką taip pat galima pavadinti statistiniu kintamuoju. (PASTABA: dirbdami kompiuteriu susipažinsime su programavimo kalbos kintamaisiais, tad atskirkite, kad „kompiuteriniai“ ir statistiniai kintamieji yra skirtingi dalykai).

Analizei svarbu atpažinti tokias duomenų sekas:

  1. statistinė seka (statistinė eilutė) – duomenys surašyti tokia eilės tvarka, kokia buvo surinkti;
  2. variacinė seka (variacinė eilutė) – duomenys išrikiuoti didėjimo (arba nemažėjimo, jei yra vienodų reikšmių) tvarka.

1.9.2 Duomenų lentelė

Potemę apie duomenų lenteles išmokite labai gerai:
duomenų lentelė – tai pagrindinė duomenų pateikimo forma.

Duomenų lentelė (angl. data table, data frame) – tai lentelės pavidalo duomenų organizavimo forma, kai eilutės skirtos tiriamiesiems (stebėjimams), o stulpeliai – kintamiesiems. Duomenų lentelė gali būti gaunama vienos ar kelių duomenų sekų reikšmes surašius kaip stulpelius. Tik svarbu, kad pirma kiekvienos sekos reikšmė apibūdintų pirmą tiriamąjį, antra – antrąjį ir t.t. T.y., svarbu, kad kiekvienos sekos reikšmių eilės tvarka atitiktų.

Tvarkingoji duomenų lentelė (angl. tidy data) – statistiniam tyrimui svarbiausia duomenų organizavimo forma. Ji yra standartizuota ir pritaikyta darbui statistinėmis programomis. Tvarkingos duomenų lentelės sudarymo principas: kiekviena eilutė skirta tik vienam stebėjimui, kiekvienas stulpelis – vienam kintamajam (savybei), o langeliuose – kiekvieno tiriamojo savybių reikšmės (žiūrėti Pav. 1.9).

Pav. 1.9. Duomenų lentelės struktūra.

Atkreipkite dėmesį, kad stulpelių pavadinimai nurodo tiriamųjų savybes. Be to, kompiuterinėse programose kiekviena lentelė turi turėti pavadinimą. Rekomenduojama lentelei suteikti prasmingą pavadinimą, kuris glaustai apibendrintų lentelėje surinktus duomenis ir/arba tyrimo esmę.

Terminas „tvarkingoji duomenų lentelė“ apibūdina duomenų pateikimo formą, bet neapibūdina turinio, pvz., ar duomenyse yra trūkstamų reikšmių.

Tvarkingųjų duomenų lentelių principai plačiau išdėstyti straipsnyje (Wickham 2014).

Užduotis 1.1  

  1. Kas yra tvarkingoji duomenų lentelė? Kas jos stulpeliuose ir kas – eilutėse?
  2. Ar tvarkingojoje duomenų lentelėje gali būti trūkstamų reikšmių?
  3. „Lenktynėse dalyvavo 8 žirgai. Juodi žirgai trasą įveikė per 3,2, 4,6 ir 4,0 min., šyvi – per 3,1 ir 4,2 min., bėri – per 3,9, 3,3, ir 4,1 min.“ Šioje pastraipoje pateiktą informaciją parašykite tvarkingosios duomenų lentelės pavidalu.

1.10 Duomenų savybės

Potemę apie statistinių duomenų tipus išmokite labai gerai: šias žinias naudosite kiekvienos būsimos temos metu.

1.10.1 Kintamieji pagal paskirtį

Šiame teorijos kurse dėmesį skirsime tik analizei skirtiems kintamiesiems. Visgi šis poskyris skirtas atkreipti dėmesį į tai, kad praktiškai ne visi duomenų lentelės kintamieji skirti analizei. Kai kurie joje yra vien tik dėl techninių priežasčių, pvz., tam, kad būtų galima atpažinti, kam priklauso duomenų eilutės duomenys, tam, kad būtų galima teisingai sujungti kelias duomenų lenteles, arba dėl kitų duomenų pertvarkymui svarbių priežasčių. Tad sąlyginai pagal paskirtį kintamuosius galima suskirstyti į:

  • techninius, kuriems teoriškai nustatyti statistinį duomenų tipą nėra svarbu;
  • analitinius, skirtus analizei, kuriems pagal statistinį (teorinį) duomenų tipą ir kitas duomenų savybes parenkame analizės metodus.

Priklausomai nuo konteksto, kartais tas pats kintamasis gali būti techninis, kartais – analitinis. Pvz., tiriamųjų vardai: techninis, jei pagal vardus sujungiami duomenys iš kelių šaltinių, analitinis, jei atliekama populiariausio vardo paieška.

Pav. 1.10. Sąlyginis kintamųjų skirstymas pagal paskirtį.

1.10.2 Tolydumas ir diskretumas

Prieš nagrinėdami duomenų tipus, išsiaiškinkime, ką reiškia terminai „diskretusis“ ir „tolydusis“:

  1. Diskretus (angl. discrete):
    • turintis baigtinį (suskaičiuojamą) galimų reikšmių skaičių;
    • turintis aiškiai skiriamas reikšmes.
  2. Tolydus (angl. continuous):
    • turintis be galo daug reikšmių, t. y. jų skaičius bet kuriame intervale yra begalinis;
    • netrūkusis (neturintis trūkio taškų).

Tam, kad geriau suprastumėte šias sąvokas, panagrinėkite Pav. 1.11 esančią iliustraciją.

Pav. 1.11. Diskretumo ir tolydumo iliustracija spalvų paletės pavyzdžiu.

Diskrečiųjų savybių turinčio kintamojo pavyzdys: studentų, lankančių biostatistikos paskaitas, skaičius gali būti tik sveikasis, pvz., 53 ar 54. Tačiau net teoriškai negali būti tarpinio varianto.

Tolydžiųjų savybių turinčio kintamojo pavyzdys: studento ūgis – tarp reikšmių 164 ir 165 cm teoriškai gali būti be galo daug tarpinių variantų, pvz., 164,35964… Nesakau, kad praktiškai galima pasiekti tokį matavimo tikslumą ar kad jis turi praktinės naudos, tačiau teoriškai galimos visos tarpinės reikšmės.

Tolydusis ≠ tolygusis.

Pastaba: statistikoje dar yra terminas „tolygusis“ – tai toks skirstinys, kurio galimos reikšmės pasitaiko vienodai dažnai (kiekvienos reikšmės įgijimo tikimybė vienoda).

1.10.3 Statistiniai duomenų tipai

Itin svarbi potemė: šias žinias naudosime dažnai.

Pagal prigimtį statistiniai kintamieji skirstomi į 2 dideles grupes: kokybinius (kategorinius plačiąja prasme) ir kiekybinius. Šie, savo ruožtu, skaidomi į 4 pagrindinius tipus (Pav. 1.12). Vieną kintamąjį sudaro to paties tipo duomenys, tad terminus „duomenų tipai“ ir „kintamųjų tipai“ naudosime kaip sinonimus.

Pav. 1.12. Pagrindiniai statistinių duomenų tipai. * – kai kuriais atvejais ranginiai duomenys interpretuojami tarsi būtų kiekybiniai.

Statistinių duomenų tipai:

  • Kokybiniai (kategoriniai) kintamieji:

    • nominalieji (angl. nominal variable; lot. nomen – pavadinimas, vardas) – tai tokie kintamieji, kurių galimų reikšmių (vadinamos kategorijomis) išdėstymo tvarka nesvarbi: reikšmės natūralios eilės tvarkos neturi. Dar vadinami pavadinimų skalės kintamaisiais. Matavimo vienetų irgi neturi. Pvz., ląstelės spalva – violetinė, raudona, melsva, bespalvė, – ląstelės forma – apvali, kvadratinė, pailga, netaisyklinga. Kartais kategorijos užkoduojamos skaičiais, pvz., 0 – sveikas, 1 – serga, bet dėl to kintamasis netampa kiekybiniu. Čia 0 ir 1 – tai tik kategorijų kodai, kurių eilės tvarka nesvarbi, su jais atlikti aritmetinius veiksmus nėra prasminga.

    • ranginiai (angl. ranked/ordered variable) – tai tokie kintamieji, kurių galimos reikšmės (vadinamos kategorijomis) turi natūralią didėjimo ar mažėjimo tvarką, tačiau atstumas tarp gretimų reikšmių nėra pastovus ar tiksliai išmatuojamas. Dar vadinami rangų skalės kintamaisiais. Įprastai matavimo vienetų neturi. Pvz., ląstelės dydžio kategorija – maža, vidutinė, didelė; savijauta – labai prasta, prasta, neutrali, gera, puiki. Ranginiams priklauso ir balais matuojami duomenys.

  • Kiekybiniai kintamieji:

    • kiekybiniai diskretieji (angl. discrete variable) – tai tokie kiekybiniai kintamieji, kurių reikšmės yra diskrečios: teigiami ir neigiami sveikieji skaičiai bei nulis. Įprastai jomis yra kas nors suskaičiuota (pvz., vyrai), tad standartiškai šie kintamieji aprašo kieno nors skaičių, pvz., ląstelių skaičių, dantų skaičių, kėdžių skaičių, į paskaitą atėjusių studentų skaičių, sėkmingų bandymų skaičių, raudonų mėgintuvėlių skaičių. Tad įprastiniai matavimo vienetai yra „vienetai“ (pvz., 15 šunų, t.y., 15 vnt.). Tokie kintamieji turi baigtinį (suskaičiuojamą) galimų reikšmių skaičių, o atstumas tarp dviejų galimų gretimų reikšmių yra pastovus ir gali būti tiksliai išmatuotas.

    • tolydieji (angl. continuous variable) – tai kiekybiniai kintamieji, kurių reikšmės yra tolydžiosios: realieji skaičiai (tarkim, 2,2354), teoriškai galintys turėti be galo daug skaitmenų po kablelio. Tad bet kuriame intervale tarp dviejų tolydžiųjų reikšmių (tarkim, tarp 2,2 ir 2,4) gali būti be galo daug skirtingų reikšmių – tolydžiųjų reikšmių skaičius yra begalinis. Nors praktiškai tolydžiuosius skaičius suapvaliname iki tam tikro tikslumo arba dėl to, kad negalime išmatuoti be galo tiksliai, arba dėl to, kad praktiniam naudojimui užtenka ir mažesnio (baigtinio) tikslumo – iš to išplaukia, kad skaičiai, kurie atrodo kaip sveikieji, iš tiesų gali būti tolydieji,– visgi teoriškai kintamasis vis tiek išlieka tolydusis.

      Tad kaip identifikuoti, kad tai tolydusis kintamasis? Įprastai šie kintamieji turi konkrečius matavimo vienetus (ląstelės svoris kilogramais, ilgis centimetrais, regėjimo aštrumas dioptrijomis, trukmė sekundėmis, kai skaičiuojamos ir sekundžių dalys), būti išreikšti kaip kelių dydžių santykis (pvz., santykis tarp ilgio metrais ir pločio metrais, vidutinis moksleivių skaičius mokyklos klasėje, kur matavimo vienetai iš tiesų yra \frac{moksleivių~skaičius}{klasių~skaičius}), ar būti bedimensiai ar santykiniais vienetais matuojami dydžiai (šviesos intensyvumas santykiniais vienetais).

Duomenų analizės metodo pasirinkimas priklauso nuo kintamojo duomenų tipo. Todėl išmokite itin greitai identifikuoti statistinius duomenų tipus.

Užduotis 1.2 Įvardinkite, kuo panašūs ir kuo skiriasi:

  1. nominalieji ir tolydieji duomenys;
  2. kiekybiniai diskretieji ir tolydieji duomenys;
  3. ranginiai ir kiekybiniai diskretieji duomenys;
  4. nominalieji ir ranginiai duomenys.

1.10.4 Duomenų tipai: praktiniai aspektai

  1. Kokius matematinius veiksmus galima atlikti su skirtingų tipų kintamųjų reikšmėmis?
    1. Nominaliąsias reikšmes galima tik suskaičiuoti: pasakyti, kiek kokių reikšmių yra.
    2. Rangines reikšmes galima suskaičiuoti, išdėstyti eilės tvarka ir palyginti, kuri didesnė/mažesnė. Bet aritmetiniai veiksmai nėra prasmingi (ar sudėjus I ir II prizinę vietą gausime III vietą?).
    3. Su kiekybinių kintamųjų reikšmėmis – skaičiais – galima atlikti iš principo visus matematinius veiksmus (suskaičiuoti, palyginti, kuri didesnė, sudėti, atimti, padauginti, padalinti, apskaičiuoti vidurkį, …).
  2. Kokie kintamieji atrodo kaip kiekybiniai, bet iš tiesų yra kategoriniai?
    1. Kategorijos, užkoduotos skaičiais, vis tiek yra kategorijos (tad joms skaičiuoti vidurkį nėra prasmės, pvz., 0 – mėlynas, 1 – rudas, 2 – žalias).
    2. Balais matuojami kintamieji iš tiesų yra ranginiai. Visgi, jei jie gali įgyti pakankamai daug skirtingų reikšmių ir jų vidurkis turi prasmę (turbūt žinote, kas yra sesijos pažymių vidurkis), dažnai interpretuojami kaip skaitiniai. Visgi reikia prisiminti, kad pagal prigimtį – tai iš eilės išdėliotos kategorijos (rangai).
  3. Kurie duomenų tipai turi diskrečių savybių?
    1. nominalieji;
    2. ranginiai;
    3. kiekybiniai diskretieji.
    • Tai bus svarbu renkantis analizės metodą.
  4. Kurie duomenų tipai turi kiekybinių savybių?
    1. tolydieji;
    2. kiekybiniai diskretieji;
    3. tik kai kuriais išimtiniais atvejais gali būti interpretuojami kaip kiekybiniai: ranginiai.
    • Tai bus svarbu renkantis analizės metodą.

Užduotis 1.3 Kuriam iš keturių tipų (nominalieji, ranginiai, diskretieji, tolydieji) priklauso šie duomenys:

  1. Šokolado svoris (g);
  2. Šokolado skonis (neskanus, skanus, labai skanus);
  3. Šokolado pakuotės spalva;
  4. Šokolado lydymosi temperatūra (°C);
  5. Šokolado plytelių skaičius;
  6. Šokolado porėtumas (porėtas/neporėtas);
  7. Šokolado rūšis (juodasis, baltasis, pieniškas, mėtinis);
  8. Šokolade esančių riešutų skaičius.

1.10.5 Reikšmių pasiskirstymas (skirstinys)

Skirstinys (angl. distribution) – tai apibūdinimas arba taisyklė, nusakanti, kiek ir kokių reikšmių yra (ar gali būti). Kiekvienas kintamasis turi skirstinį. Įprastai skirstiniai nurodo galimą reikšmę (ar jų intervalą) bei su tuo susietą reikšmių skaičių (statistinį dažnį), (procentinę) dalį arba tikimybę.

Skirstinys nurodo, kiek kokių reikšmių yra.

Dažnai:

Skirstinys = reikšmės ir jų dažniai.
Skirstinys = reikšmės ir jų įgijimo tikimybės.

Skirstiniai būna:

  • Empiriniai – sudaryti iš tyrimo duomenų ir atspindintys faktinį pasiskirstymą;
  • Teoriniai – matematiniai modeliai, parodantys, kaip idealiai turėtų skirstytis reikšmės esant tam tikroms sąlygoms bei galiojant tam tikroms prielaidoms.

Apibūdinant pasiskirstymą, galima naudoti:

  • grafikus;
  • lenteles;
  • formules (tik teoriniams skirstiniams).

Apibūdinti skirstinio dalį ar tam tikrą bruožą galima teiginiais: „10 iš grupės D“, „20 didesnių už 35 cm“, …

Terminai „pasiskirstymas“ ir „skirstinys“ yra sinonimai.

1.10.6 Trūkstamos reikšmės

Trūkstama reikšmė (praleistoji reikšmė; angl. missing value) – tai nežinoma, negalima arba neegzistuojanti kintamojo reikšmė. Dažnai tyrimuose žymima NA (angl. not available) arba kitu specialiuoju žymėjimu (pvz., simboliu, žodžiu, fraze, skaičiumi).

Pilnieji stebėjimai (pilnieji atvejai; angl. complete cases) – tai duomenų lentelės eilučių (stebėjimų, atvejų) skaičius be trūkstamų reikšmių.

Klausimai savikontrolei

Užduotis 1.4  

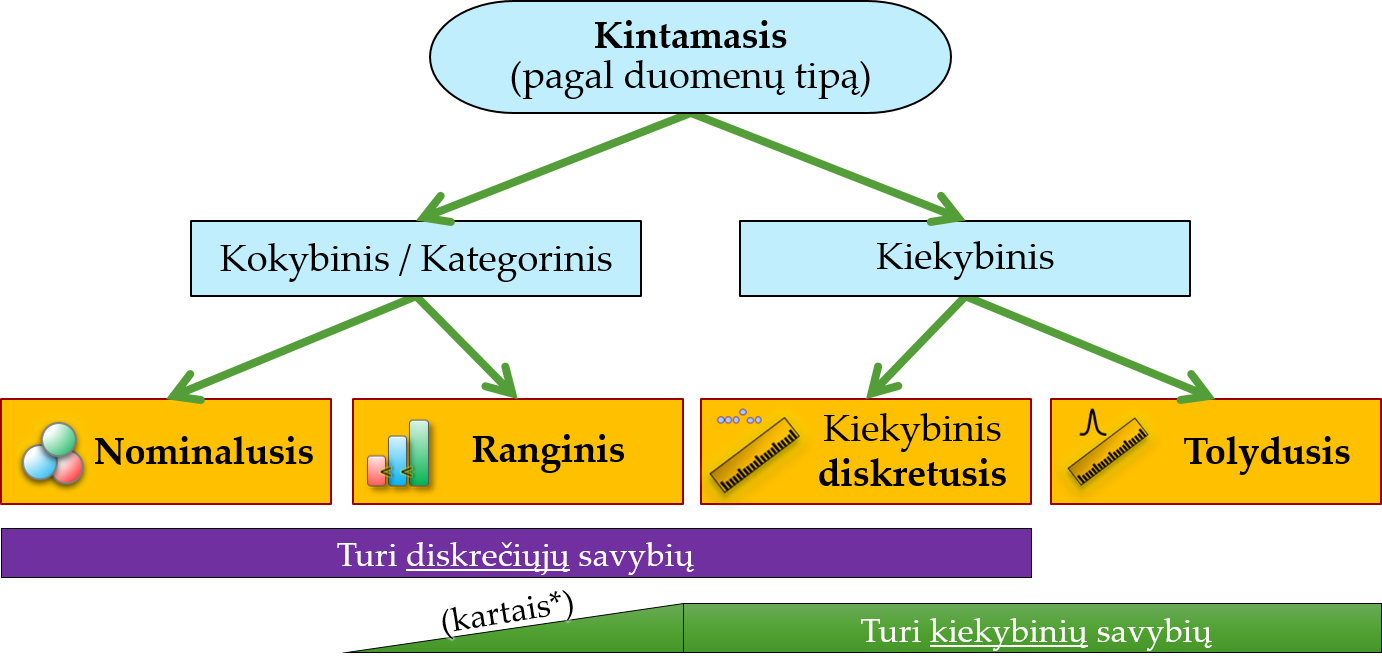
  1. Kurio duomenų tipo reikšmės negali turėti variacinės sekos?
  2. Kas yra statistika ir biostatistika? Kuo skiriasi?
  3. Kaip statistika skirstoma pagal taikymo sritis?
  4. Kaip statistika skirstoma pagal analizės metodų grupes?
  5. Kas yra kintamasis?
  6. Kas yra statistinis vienetas?
  7. Kas yra trūkstama reikšmė?
  8. Apibūdinkite kiekvieną statistinių duomenų tipą nurodydami bent po 2-3 jiems būdingas charakteristikas.
  9. Kuo informacija skiriasi nuo duomenų?
  10. Kokios tiriamųjų aibės yra statistikoje? Kuo skiriasi? Kam naudojamos?
  11. Kokiomis savybėmis pasižymi tvarkingosios duomenų lentelės?
  12. Kas yra „pasiskirstymas”?
  13. Kas yra „stebėjimas” ir kas yra „pilnasis stebėjimas“?
  14. Kuriam statistinių duomenų tipui priklauso:
    1. Kompiuterio storis (mm);
    2. Batų dydis;
    3. Telefono numeris;
    4. Kompiuterių skaičius konkrečiuose namuose;
    5. Vidutinis kompiuterių skaičius universiteto auditorijoje.

  1. Terminas „pasiskirstymas“ apibūdina, kiek kokių reikšmių yra.↩︎

  2. Kuo mažesnis neapibrėžtumas, tuo didesnis tikslumas ir patikimumas.↩︎

  3. EDA (angl. exploratory data analysis) – žvalgomoji analizė.↩︎

  4. Terminas „stebėjimas“ labiau įprastas statistikoje, o „įrašas“ – duomenų bazių terminijoje.↩︎