6. Atsitiktiniai dydžiai ir jų skirstiniai

Atlikdami tyrimą įprastai iš imties, kuri yra mažesnė už generalinę aibę (GA), mes norime daryti išvadas apie visą GA. Tokios išvados vadinamos statistinėmis išvadomis. Statistinių išvadų darymo metodai grindžiami tikimybių teorijos dėsniais ir aksiomomis. Šiame skyriuje susipažinsime su svarbiausiomis šiam kursui tikimybių teorijos sąvokomis. Daugiausiai dėmesio skirsime atsitiktiniams dydžiams ir skirstiniams.

Šiame skyriuje susipažinsime su svarbiausiomis šiam kursui tikimybių teorijos sąvokomis.

Plačiau temos apie tikimybių teorijos elementus, taikomus statistikoje, yra išdėstytos vadovėliuose (Čekanavičius ir Murauskas 2006, p.67–110; Venclovienė 2010, p.39–70).

6.1 Tikimybiniai eksperimentai ir atsitiktiniai įvykiai

Viena iš tikimybių teorijos sąvokų yra tikimybinis eksperimentas. Tai toks eksperimentas, kuris gali turėti keletą galimų baigčių, bet negalima iš anksto pasakyti, kuri konkreti baigtis įvyks šį kartą (baigtis yra atsitiktinė). Kiekvieno tikimybinio eksperimento rezultatas vadinamas atsitiktiniu įvykiu (toliau vadinsime tiesiog įvykiu). Pvz., eksperimentas – auginama ląstelė, įvykis – ląstelė užaugo; eksperimentas – tiriama kūdikio lytis, įvykis – lytis yra mergaitė; eksperimentas – 3 dienas daiginama 10 sėklų, įvykis – po 3 dienų 8 sėklos sudygo ir dvi – ne; eksperimentas – ieškomas tinkamas organų donoras, įvykis – (jei donoras rastas iš antro karto) pirmas donoras – netinkamas, antras – tinkamas; eksperimentas – sportininkas šauna į taikinį, įvykis – į taikinį buvo pataikyta; eksperimentas – atliekamas standartizuotas kraujo krešumo tyrimas, įvykis – kraujas sukrešėjo per 4 minutes.

(Atsitiktinis) įvykis – tai tikimybinio eksperimento rezultatas.

Įvykiai gali susidėti iš kelių elementariųjų įvykių. Elementarieji įvykiai yra tokie, kurie negali būti suskaidyti į mažesnes dalis. Sakykime, tiriama gimusių dvynukų lytis (eiliškumas nesvarbu) ir tokiu atveju kiekvienas vaikas turi savo lytį, tad galimi elementarieji įvykiai yra: „du berniukai“ (BB), „dvi mergaitės“ (MM) bei „berniukas ir mergaitė“ (BM). Įvykis „bent viena mergaitė“ būtų sudėtinis, nes jis apima kelis elementariuosius (MM ir BM).

Užduotis 6.1

Kas tikimybių teorijoje vadinama eksperimentu ir kas – įvykiu?
Kokie atsitiktiniai įvykiai gali įvykti šiose situacijose:
1. atliekamas Laimo ligos tyrimas;
2. matuojamas kraujospūdis;
3. tiriama gimusių trynukų lytis;
4. tiriama antocianinų tirpalo sugertis ties 450 nm.

6.2 Atsitiktinis dydis

„Atsitiktiniai dydžiai“ – labai svarbi potemė.

Kita tikimybių teorijos sąvoka – atsitiktinis dydis (trumpinsime ats.d., angl. random variable). Atsitiktinis dydis yra tam tikra funkcija (taisyklė), pagal kurią kiekvienam atsitiktiniam įvykiui priskiriama viena iš anksto nežinoma skaitinė reikšmė.

Atsitiktinis dydis nusako taisyklę, kaip atsitiktiniam įvykiui (žymima $s_i$) priskiriama skaitinė reikšmė (žymima $X(s_i)$).
[Iliustracijos šaltinis (nuoroda).](http://www.est.uc3m.es/icascos/eng/probability_notes/discrete-random-variables.html)

Pav. 6.1: Atsitiktinis dydis nusako taisyklę, kaip atsitiktiniam įvykiui (žymima $s_i$) priskiriama skaitinė reikšmė (žymima $X(s_i)$). Iliustracijos šaltinis (nuoroda).

Pavyzdžiai (eksperimentas → atsitiktinis dydis → taisyklė, pagal kurią sukuriame apibūdintą atsitiktinį dydį):

tiriame augalų aukštį, ats.d. – augalo aukštis (centimetrais), taisyklė – priskiriame tiesiogiai be perskaičiavimo;
ištiriame n baltymo molekulių (registruojant, ar jos pažeistos), ats.d. – pažeistų molekulių skaičius, taisyklė – suskaičiuojame dominančio rezultato dažnį;
pasėjame 20 sėklų ir daiginame 3 dienas, ats.d. – sudygusių sėklų skaičius iš 20 pasodintų, taisyklė – suskaičiuojame dominančio rezultato dažnį, tenkantį 20-čiai pasodintų sėklų;
ieškome tinkamo donoro (tikriname, tinka ar netinka, jei netinka, ieškome toliau), ats.d. – patikrintų donorų skaičius iki tol, kol randame tinkamą, taisyklė – suskaičiuojame, kiek donorų netiko;
tiriame (skaičiuojame) parazitus tam tikroje paukščių populiacijoje, ats.d. – vidutinis parazitų skaičius, kuris tenka vienam individui, taisyklė – apskaičiuojame vidurkį;
tiriame kraujo krešumą, ats.d. – laikas, per kurį sukreša kraujas, taisyklė – priskiriame tiesiogiai be perskaičiavimo;
tiriame (registruojame) ląstelių formą, ats.d. – apvalių ląstelių skaičius, taisyklė – suskaičiuojame mus dominančio rezultato dažnį;
sportininkas per varžybas šauna į taikinį 5 kartus, ats.d. – surinktų taškų skaičius, taisyklė – pagal varžybų taisykles suskaičiuojame surinktų taškų skaičių;
tiriame žmonių svorį, ats.d. – vidutinis svoris;
tiriame žmonių svorį, ats.d. – svorio standartinis nuokrypis;
tiriame žmonių svorį, ats.d. – skirstinio asimetrijos koeficiento reikšmė.

Kaip matome, atsitiktiniai dydžiai turi analogiškus pavadinimus, kaip ir įprasti kintamieji („surinktų taškų skaičius“, „vidutinis svoris“, „laikas, per kurį sukreša kraujas“, „sudygusių sėklų skaičius iš 20 pasodintų“, …), tik jų įgyjamos reikšmės visada yra skaičiai. Jei tiriamas dydis (matyt, jo ir dydžiu vadinti negalima) nėra išreiškiamas kaip skaičius (pvz., lapo forma) – tai nėra atsitiktinis dydis.

Atsitiktinio dydžio įgyjamos reikšmės visada yra skaičiai.

Tam, kad matematikoje išvengtume labai ilgų atsitiktinių dydžių pavadinimų, juos įprastai žymime didžiosiomis raidėmis (pvz., $X$ gali būti vartojamas vietoje „ilgis“). Konkreti reikšmė, kurią ats.d. įgyja konkretaus bandymo metu, vadinama atsitiktinio dydžio realizacija (angl., observed value, realization) ir ji įprastai žymima mažosiomis raidėmis (tarkime, rašome $x$ vietoje „6 cm“). Tad, pvz., „ilgis“ yra atsitiktinis dydis, o „6 cm“ – nebe.

Atsitiktinio dydžio žymėjimas, pvz., $X$, – tai tarsi kiekybinio kintamojo pavadinimas. Ats.d. realizacija, pvz., $x$, tai konkretus skaičius (ne atsitiktinis dydis).

Atsitiktinio dydžio $X$ vidurkis žymimas $\mathbf{E}X$ (nuo angliško termino expected value), o dispersija – $\mathbf{D}X$. Skaičiai būna diskretieji arba tolydieji, todėl ir atsitiktiniai dydžiai taip pat būna arba diskretieji, arba tolydieji (pav. 6.2).

Ar įžvelgiate analogiją tarp diskrečiųjų ats.d. bei diskrečiųjų spalvų skalės $(A)$ ir tarp tolydžiųjų ats.d. bei tolydžiai (gradientiškai) kintančių spalvų skalės $(B)$?

Pav. 6.2: Ar įžvelgiate analogiją tarp diskrečiųjų ats.d. bei diskrečiųjų spalvų skalės $(A)$ ir tarp tolydžiųjų ats.d. bei tolydžiai (gradientiškai) kintančių spalvų skalės $(B)$?

Kam mums reikalingi atsitiktiniai dydžiai? Jei dydis yra išreikštas kaip skaičius, su juo galime atlikti aritmetines operacijas, jį lengviau panaudoti skaičiavimuose. Tad ats.d. yra labiau matematizuoti nei atsitiktiniai įvykiai. Ats. dydžiams galime parinkti matematinius modelius, o tie patys modeliai įprastai tinka daugeliui situacijų bei eksperimentų. Dėl to teorinių modelių, skirtų aprašyti ats.dydžius, kuriuos naudojame statistiniams skaičiavimams, nėra tiek jau daug. Apie tai plačiau kalbama dalyje „6.4.3 Teoriniai skirstiniai“ ir tolimesniuose poskyriuose.

Daugiau apie atsitiktinius dydžius galite sužinoti video paskaitų cikle „Random variables“ (anglų kalba su subtitrais, kurių reikia ieškoti kortelėje „Transcript“). Visiems rekomenduoju peržiūrėti bent pirmąją dalį, kurios trukmė ~ 6 min (šios dalies YouTube versija rodoma epizode 6.1).

Video epizodas 6.1 Atsitiktiniai dydžiai (angl. random variables).

Taip pat rekomenduoju perskaityti vadovėlyje (Čekanavičius ir Murauskas 2006, p.87–89, sk.11) esantį skyrių apie atsitiktinius dydžius.

Užduotis 6.2 Nustatykite, kas aprašyta kiekviename sąrašo punkte: tolydusis atsitiktinis dydis (T), diskretusis atsitiktinis dydis (D), ne atsitiktinis dydis (N).

Tiriamų ląstelių branduolio tūris;
Branduolių skaičius ląstelėje;
Audinio tipas, kuriam priklauso ląstelė;
Laikas, per kurį ląstelė pasidalina (minutėmis);
Sudygusių daigų aukštis;
Sudygusio daigo atspalvis (balsvas / žalsvas);
Nesudygusių daigų skaičius;
Tyrėjo lytis.

6.3 Tikimybė

Tikimybė (angl. probability) – matas, kiekybiškai įvertinantis tam tikros atsitiktinės tikimybinio eksperimento baigties (įvykio) galimybę. Kinta nuo 0 (negalimas įvykis, kuris neįvyks) iki 1 (būtinasis įvykis, kuris tikrai įvyks). Tikimybė dažnai žymima kaip funkcija $P$. Jei $A$ yra mus dominantis įvykis, sakykime, $A$ – gims mergaitė, tada užrašas „$P(A)$“ nurodo tikimybę, kad gims mergaitė, pvz., $P(A) = 0{,}49$. Užrašas $P(X = x) = 0{,}1$ reikštų, kad tikimybė, jog atsitiktinis dydis ($X$ didžioji, sakykime, kolonijų skaičius) bus lygus konkrečiam skaičiui ($x$ mažoji, tarkime, 20), lygi $0{,}1$, t.y., 10%. Tikimybė gali būti užrašoma kaip skaičius tarp 0 ir 1 arba procentine išraiška nuo 0% iki 100%. Jei nepasakyta kitaip, statistiniuose skaičiavimuose tikimybę užrašykite kaip skaičių tarp 0 ir 1, o ne procentais.

Apie terminų vartojimą: terminas „tikimybė“ yra tinkamesnis kalbant apie generalinę aibę. O kalbant apie imties duomenis, tinkamesnis atitikmuo būtų „santykinis dažnis“.

Tikimybė (jei generalinė aibė) ↔︎ Santykinis dažnis (jei imtis)

6.3.1 Statistinis tikimybės apibrėžimas

Sakykime, kad eksperimentą atliekame $n$ kartų. Mus dominanti baigtis (tarkime, įvykis $A$) įvyksta $m$ kartų. Statistine įvykio tikimybe vadinamas skaičius $P(A)$, apie kurį telkiasi santykis $m/n$ esant dideliam eksperimentų skaičiui:

\[\begin{equation} P(A) = \lim \limits_{n \to \infty} \left( \frac{m}{n} \right) \tag{6.1} \end{equation}\]

Pavyzdys. Stebime $n = 30000$ atsitiktinai pasirinktų moterų, kurios rengiasi gimdyti. Sakykime, kad gimė $m$ berniukų ir $n - m$ mergaičių. Tada gauname $P(gimė~berniukas) = m/n$.

Praktiškai gana retai būna tokios situacijos, kad bandymą galėtume atlikti labai daug kartų. Todėl skaičiavimui statistinis tikimybės apibrėžimas taikomas retai. Tačiau jis labai parankus interpretuoti rezultatus: sakykime, jei gauname tikimybę $0{,}4$, tai reiškia, kad įvykis įvyksta 2 kartus iš 5.

6.3.2 Klasikinis tikimybės apibrėžimas

Sakykime, kad mus dominantį įvykį $A$ sudaro $k$ elementariųjų įvykių iš $n$ galimų. Visų elementariųjų įvykių tikimybės yra vienodos. Tada įvykio $A$ tikimybė apibrėžiama lygtimi (6.2). Tai ir yra klasikinis tikimybės apibrėžimas.

\[\begin{equation} P(A) = \frac{k}{n} \tag{6.2} \end{equation}\]

Prielaida: visi elementarieji įvykiai yra vienodai galimi. Konkrečiu atveju ši prielaida gali būti klaidinga.

Pavyzdys. Darykime prielaidą, kad įvykiai „gimė berniukas“ ir „gimė mergaitė“ yra vienodai galimi (pastaba: realybėje taip nėra). Šioje situacijoje yra du elementarieji įvykiai, o mus domina tik vienas. Taikydami klasikinį tikimybės apibrėžimą gautume, kad $P(gimė~berniukas) = 1/2$.

Klasikinis tikimybės apibrėžimas tinkamas tik tada, jei elementariųjų įvykių skaičius yra baigtinis (pvz., situacijoje, kai ieškomas donoras iki tol, kol bus rastas tinkamas, elementariųjų įvykių gali būti be galo daug) ir visų jų įgijimo tikimybės yra vienodos.

6.3.3 Klasikinės tikimybės taikymas uždaviniams spręsti

Sprendžiant uždavinius, kurių metu taikomas klasikinis tikimybės apibrėžimas, visų galimų ar mus dominančių elementariųjų įvykių skaičius dažnai nustatomas pagal kėlinių, gretinių, derinių formules arba kombinatorinę daugybos taisyklę.

Kėliniai² $(P_n)$ parodo, keliais skirtingais būdais galima išdėstyti $n$ objektų, kai objektai nesikartoja.

\[\begin{equation} P_n = n! \tag{6.3} \end{equation}\]

$n$ – objektų skaičius iš viso, $!$ – faktorialas.

Gretiniai be pasikartojimo ³ $(A^k_n)$ – junginiai, gauti iš $n$ objektų išrinkus $k$ skirtingų atsižvelgiant į jų išrinkimo tvarką. T.y., gretiniai parodo, keliais būdais tam tikra eilės tvarka galime išdėlioti $k$ objektų, kai galime rinktis iš $n$ objektų. Objektai nesikartoja, tačiau išdėstymo eilės tvarka yra svarbi bei $1 \leq k \leq n$.

\[\begin{equation} A^k_n = \frac{n!}{(n-k)!} \tag{6.4} \end{equation}\]

Deriniai⁴ $(C^k_n)$, alternatyvus žymėjimas $\binom{n}{k}$ – junginiai, gauti iš $n$ objektų išrinkus $k$ skirtingų neatsižvelgiant į jų išrinkimo tvarką. T.y., deriniai parodo, keliais būdais bet kokia eilės tvarka galime išdėlioti $k$ objektų, kai galime rinktis iš $n$ objektų. Objektai nesikartoja, išdėstymo eilės tvarka nesvarbi bei $1 \leq k \leq n$.

\[\begin{equation} C^k_n = {n \choose k} = \frac{n!}{k!(n-k)!} \tag{6.5} \end{equation}\]$k$ – pasirinktų objektų skaičius.

Lygtyje (6.5) apibrėžiamas koeficientas dar vadinamas binominiu koeficientu (nuo jo kilęs ir binominio skirstinio pavadinimas, žr. skyriuje „6.5.1 Binominis skirstinys“).

Kombinatorinė daugybos taisyklė – tai bendras metodas apskaičiuoti, keliais būdais galima išdėstyti objektus, kai turime $l$ pozicijų ir kai žinome, kiek variantų $(n_i)$ galima turėti kiekvienoje pozicijoje $(i \in 1, ~2, ~...~, ~l)$:

\[\begin{equation} (n_1)(n_2)(n_3)...(n_l) \tag{6.6} \end{equation}\]Čia $l$ – pozicijų skaičius.

Užduotis 6.3

Įprastinius Lietuvoje registruotų automobilių numerius sudaro trys lotyniškos raidės (23 galimi raidžių variantai) ir trys skaitmenys (10 skaitmenų variantų). Automobilio numeryje vienintelė negalima skaičių kombinacija yra „000“. Kiek skirtingų įprastinių leistinų automobilio numerių variantų galima sudaryti?
Biologinę sistemą veikia 3 veiksniai. Registruotas kiekvieno jų silpnas ir stiprus poveikiai. Vienas objektas gali būti ištirtas tik vieną kartą. Kiek mažiausiai tyrimo objektų reikės, kad būtų ištirta kiekviena galima veiksnių kombinacija?

6.4 Skirstiniai

Skirstiniai gali būti empiriniai (gauti iš duomenų) ir teoriniai (idealizuoti, įprastai aprašomi teorinėmis lygtimis). Šioje dalyje kalbėsime apie pastaruosius. Tad atsitiktinio dydžio reikšmių skirstinys (angl. probability distribution), arba tiesiog skirstinys, – yra apibūdinimas arba taisyklė, susiejanti atsitiktinio dydžio reikšmes su jų įgijimo tikimybėmis. Skirstinys gali būti pateiktas kaip formulė, lentelė arba grafikas. Priklausomai nuo ats.d. tipo, skirstiniai skirstomi į diskrečiuosius ir tolydžiuosius.

Atsitiktinio dydžio skirstinys – tai atsitiktinio dydžio reikšmės ir su jomis susietos tikimybės.

6.4.1 Skirstinių pateikimo formos

Diskrečiaisiais skirstiniais vadinami skirstiniai, jei jie aprašo diskrečiuosius atsitiktinius dydžius, tolydžiaisiais, jei tolydžiuosius.

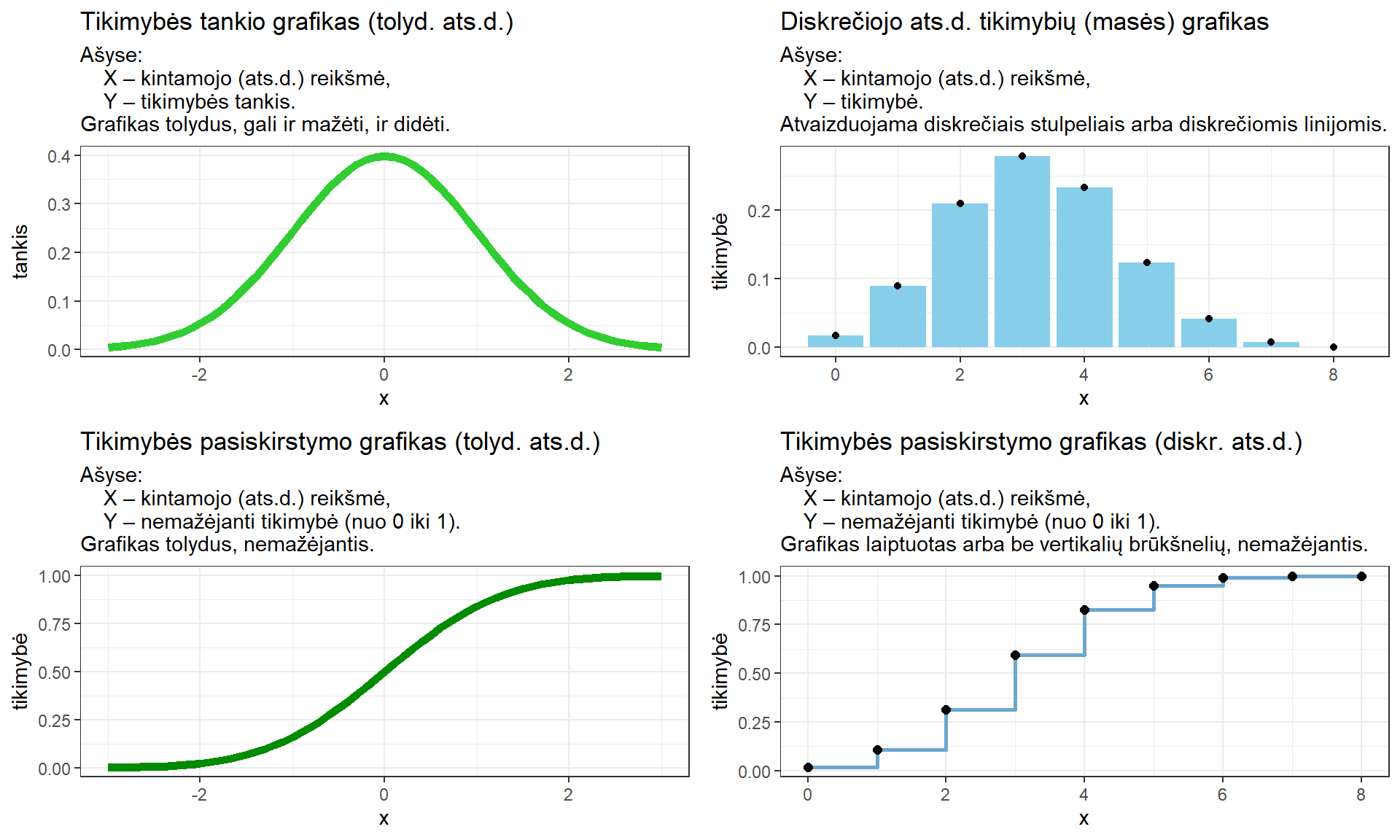
Diskrečiųjų ir tolydžiųjų skirstinių formos ir paaiškinimai, kaip jas atpažinti. Taškai žymi konkrečias ats.d. reikšmes ir su jomis susietas tikimybes.

Pav. 6.3: Diskrečiųjų ir tolydžiųjų skirstinių formos ir paaiškinimai, kaip jas atpažinti. Taškai žymi konkrečias ats.d. reikšmes ir su jomis susietas tikimybes.

Kiekvienas skirstinys gali būti pateiktas dviem formomis (pav. 6.3):

jei skirstinys diskretusis:
1. tikimybių (tikimybės masės) funkcija (pvz., santykinių dažnių lentelė) – parodo konkrečios reikšmės įgijimo tikimybę, kuri įprastai žymima $P(X = x)$;
2. diskrečioji pasiskirstymo funkcija (pvz., sukauptųjų santykinių dažnių lentelė) – parodo tikimybę įgyti reikšmę, ne didesnę už kitą konkrečią reikšmę, vadinamą kvantiliu. Pasiskirstymo funkcija įprastai žymima $F(x)$, kur $x$ yra kvantilis, ir yra lygi išraiškai $P(X \le x)$ (tikslesnis kvantilio apibrėžimas pateiktas skyriuje 6.4.2).
jei skirstinys tolydusis:
1. tikimybės tankio funkcija (ar pamenate branduolių tankio grafiką?) – pasirinktame ats.d. reikšmių intervale plotas po šia kreive parodo tikimybę ats.d. reikšmei patekti į intervalą;
2. tolydžioji pasiskirstymo funkcija – analogiškai kaip ir diskrečiojo skirstinio atveju, parodo tikimybę įgyti reikšmę, ne didesnę už kitą konkrečią reikšmę, vadinamą kvantiliu, taip pat žymima $F(x)$ ir yra lygi $P(X \le x)$.

Detaliau sąsaja tarp skirstinio pateikimo formų nagrinėjama pav. 6.4 ir 6.5.

Trumpas matematinių užrašų, tokių kaip $F(x)$, $P(X=x)$, $P(X<x)$, paaiškinimas. Sakykime, kad atliekame kūdikių svorio tyrimą. Užrašas $F(3~kg)$ atitiktų užrašą $P(Svoris \le 3~kg)$ bei sakinį „tikimybė, kad kūdikio svoris, tiriamasis atsitiktinis dydis $X$, bus ne didesnis už $3~kg$, t.y., už konkretų skaičių $x$“. Šiuo atveju $3~kg$ yra atsitiktinio dydžio kvantilis.

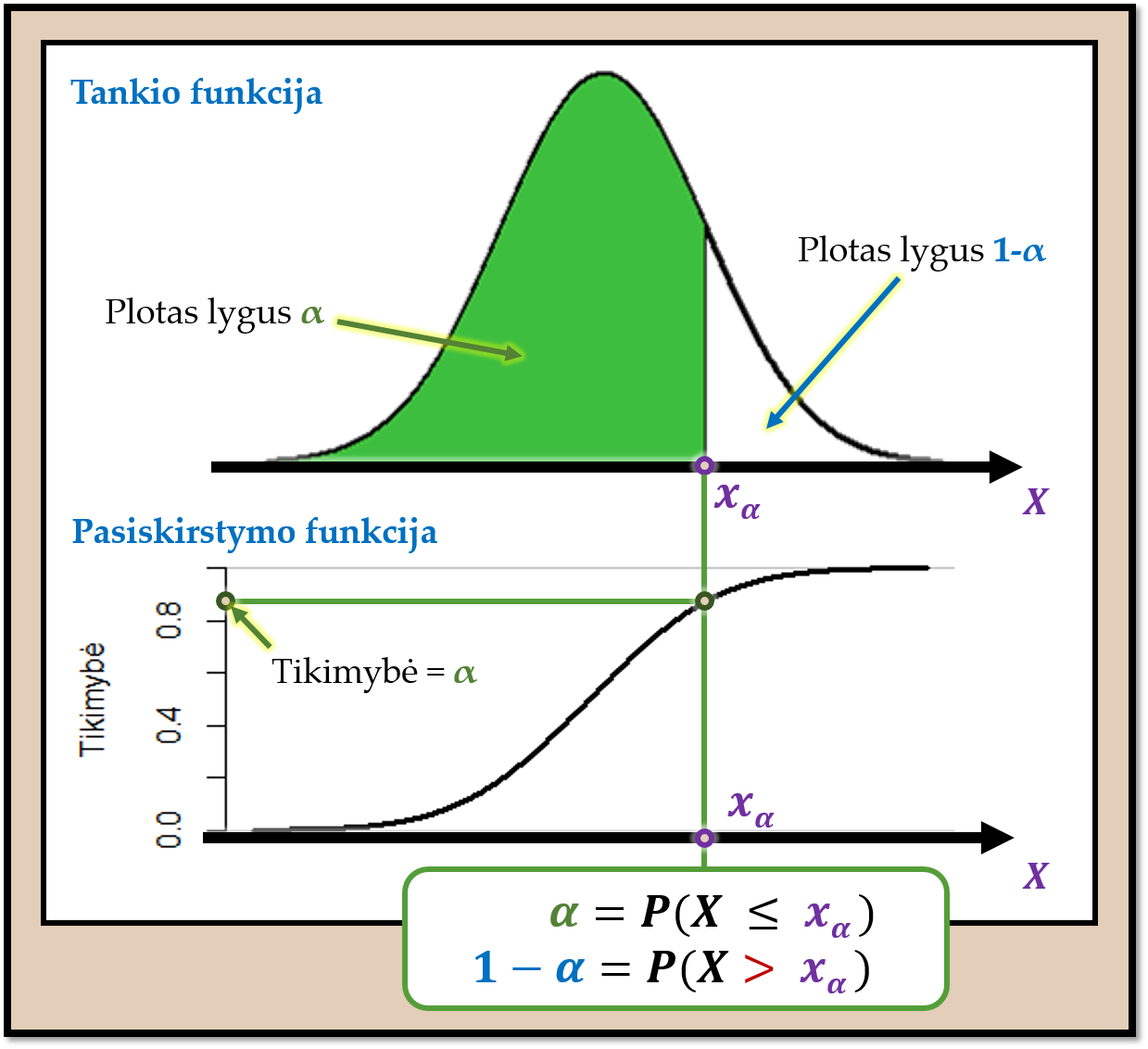
$Sąsaja tarp tolydžiojo ats.d. $X$ kvantilio $x_\alpha$, su juo susietos tikimybės $\alpha$ bei tikimybės tankio ir tikimybės pasiskirstymo grafikų. Plotas po tankio grafiko kreive tam tikrame intervale nurodo tikimybę, kuri matoma ir pasiskirstymo funkcijos y ašyje. Plotas po visa tankio kreive lygus 1, tokio dydžio yra ir maksimali pasiskirstymo funkcijos y ašies reikšmė. Vaizduojamas normaliojo skirstinio pavyzdys.$

Pav. 6.4: Sąsaja tarp tolydžiojo ats.d. $X$ kvantilio $x_\alpha$, su juo susietos tikimybės $\alpha$ bei tikimybės tankio ir tikimybės pasiskirstymo grafikų. Plotas po tankio grafiko kreive tam tikrame intervale nurodo tikimybę, kuri matoma ir pasiskirstymo funkcijos y ašyje. Plotas po visa tankio kreive lygus 1, tokio dydžio yra ir maksimali pasiskirstymo funkcijos y ašies reikšmė. Vaizduojamas normaliojo skirstinio pavyzdys.

$Sąsaja tarp diskrečiojo ats.d. $X$ kvantilio $x_{\alpha}$, su juo susietos tikimybės $\alpha$ bei tikimybių (masės) ir tikimybės pasiskirstymo grafikų. Čia $i$ -- reikšmės eilės numeris x ašyje. Vaizduojamas binominio skirstinio pavyzdys.$

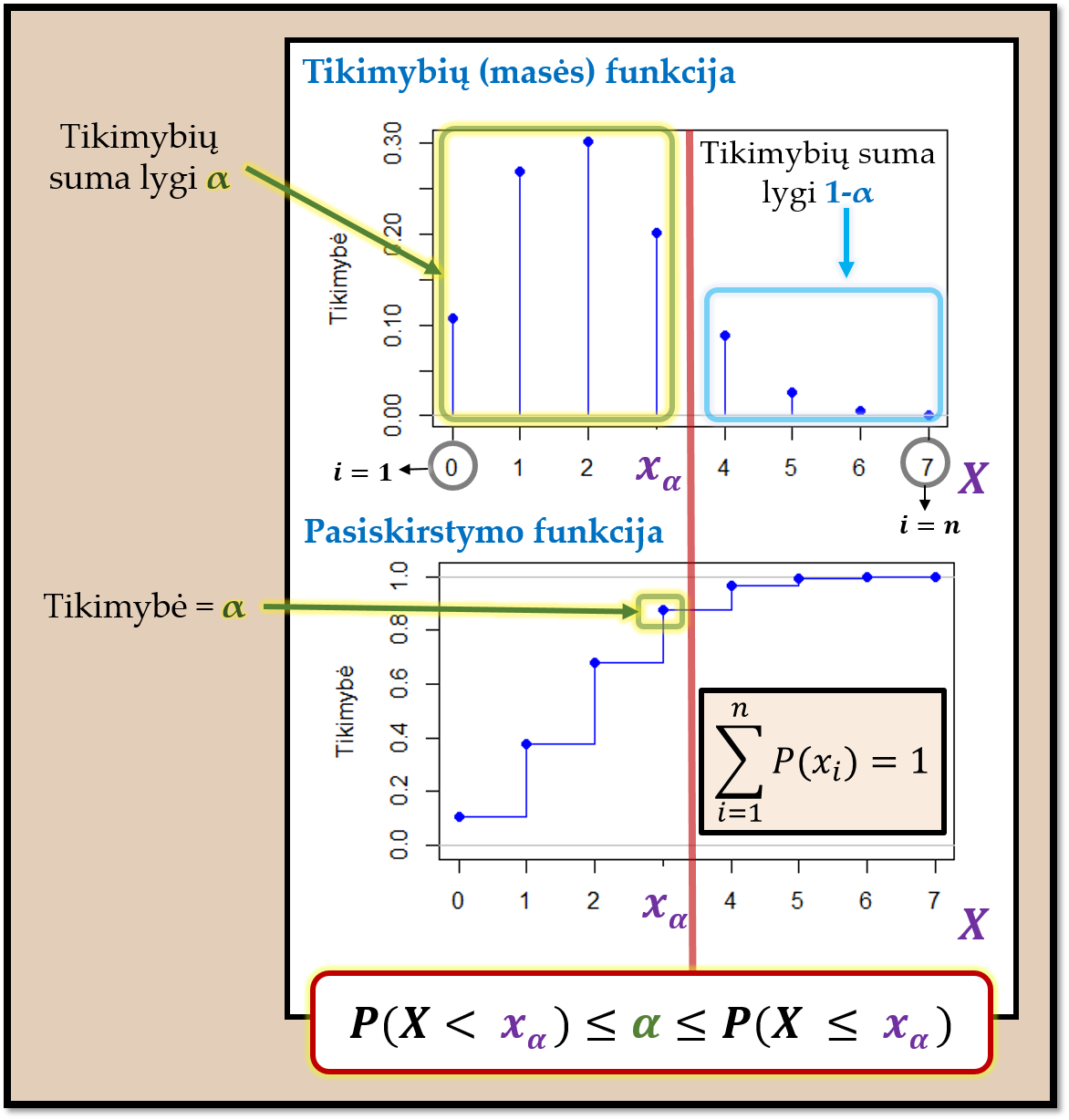
Pav. 6.5: Sąsaja tarp diskrečiojo ats.d. $X$ kvantilio $x_{\alpha}$, su juo susietos tikimybės $\alpha$ bei tikimybių (masės) ir tikimybės pasiskirstymo grafikų. Čia $i$ – reikšmės eilės numeris x ašyje. Vaizduojamas binominio skirstinio pavyzdys.

Užduotis 6.4

Kaip pagal grafiko kreivės formą atskirti tolydžiojo ir diskrečiojo ats.d. pasiskirstymo funkcijas?

6.4.2 Kvantiliai

Atsitiktinio dydžio kvantilis – tai atsitiktinio dydžio reikšmė, susieta su tikimybe „ne daugiau už“.

Bendruoju atveju atsitiktinio dydžio $\alpha$ eilės kvantilis yra skaičius $x_{\alpha}$, kuris tenkina tokią nelygybę ($\alpha$ yra tikimybė):

\[\begin{equation} P(X < x_{\alpha}) \le \alpha \le P(X \le x_{\alpha}) \tag{6.7} \end{equation}\]

Diskrečiuoju atveju dėl diskretumo kartais iš pirmo žvilgsnio gali pasirodyti dviprasmiška, kurį skaičių laikyti kvantiliu, todėl nelygybės neišvengsime: panagrinėkite pav. 6.6 pateiktą binominio (diskretusis) skirstinio pavyzdį. Visgi, reikia žinoti, kad $x_{\alpha}$ yra mažiausia ats.d. reikšmė, tenkinanti nelygybę:

\[\begin{equation} \alpha \le P(X \le x_{\alpha}) \tag{6.8} \end{equation}\]

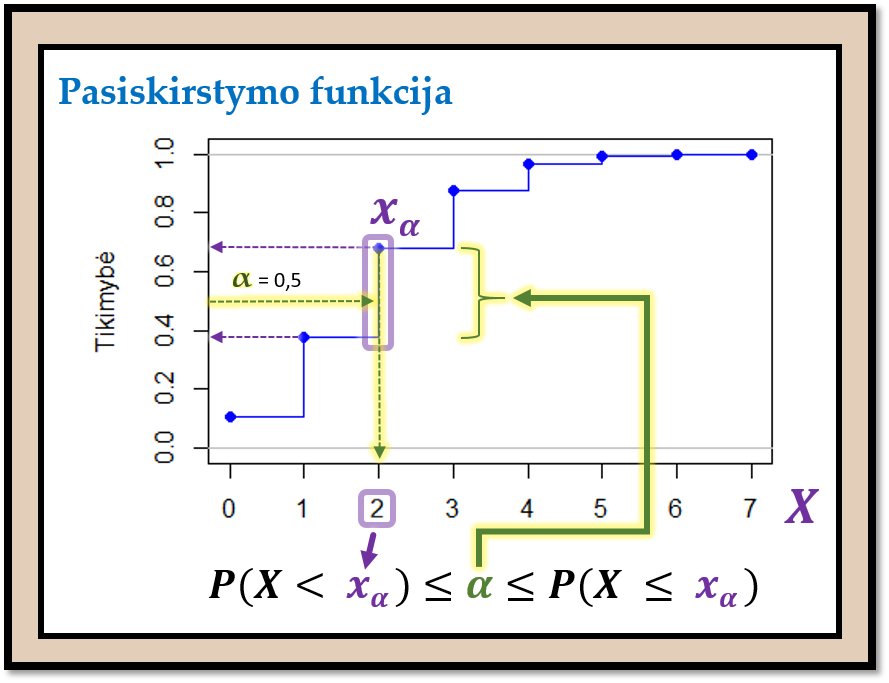
$Nelygybės \@ref(eq:ats-d-kvantilis) taikymo pavyzdys, kai diskrečiojo skirstinio atveju norima surasti kvantilį $x_{\alpha}$ ir duota, kad $\alpha = 0{,}5$. Pavaizduota binominio skirstinio $X \sim \mathcal{B}(n = 7; p = 0{,}25)$ pasiskirstymo funkcija. Gauname, kad $x_{0{,}5}=2$. Pastebėkite, kad kai skirstinys diskretusis, tą patį skaičių x ašyje atitinka visas $\alpha$ reikšmių intervalas.$

Pav. 6.6: Nelygybės (6.7) taikymo pavyzdys, kai diskrečiojo skirstinio atveju norima surasti kvantilį $x_{\alpha}$ ir duota, kad $\alpha = 0{,}5$. Pavaizduota binominio skirstinio $X \sim \mathcal{B}(n = 7; p = 0{,}25)$ pasiskirstymo funkcija. Gauname, kad $x_{0{,}5}=2$. Pastebėkite, kad kai skirstinys diskretusis, tą patį skaičių x ašyje atitinka visas $\alpha$ reikšmių intervalas.

Tolydžiuoju atveju konkretaus skaičiaus įgijimo tikimybė lygi nuliui:

\[\begin{equation} P(X = x_{\alpha}) = 0 \tag{6.9} \end{equation}\]

Todėl nelygybę (6.7) tolydiesiems ats.d. galima supaprastinti:

\[\begin{equation} \alpha = P(X < x_{\alpha}) \tag{6.10} \end{equation}\]

Užduotis 6.5

Naudodami pav. 6.6 nustatykite, kam lygus paveiksle vaizduojamo skirstinio $\alpha = 0{,}8$ lygmens kvantilis.

6.4.3 Teoriniai skirstiniai

Atsitiktiniai dydžiai įprastai gali būti aprašyti vienu iš kelių žinomų teorinių skirstinių, kurie modeliuoja tam tikrus procesus. Pvz., tolydieji ats.d. gali būti aprašomi normaliuoju (Gauso), log-normaliuoju, diskretieji – Puasono, binominiu, geometriniu, neigiamu binominiu ir kitais. Į teorinių skirstinių naudojimą galima žiūrėti kaip į mokslinį įrankį, skirtą įvertinti tikimybinių reiškinių neapibrėžtumą, apskaičiuoti paklaidas, analizuoti procesų kilmę (ar atitinka modelį, ar ne), atlikti kitokius skaičiavimus, kurie leistų priimti statistiniu modeliavimu pagrįstus sprendimus. Tarkime, jei modelis imties duomenims tinka pakankamai gerai, tada tarsi teigiama, kad modeliu aprašomas skirstinys būdingas generalinei aibei ir pagal jį galima daryti prognozes.

Skirstiniai gali būti taikomi tokiose srityse, kaip:

tikimybinių reiškinių, atsitiktinių dydžių modeliavimas (pvz., apskaičiuoti, kokia tikimybė, kad jūs turėsite bent 2 vaikus);
pasikliautinųjų intervalų sudarymas (pvz., iš apklausos duomenų su tam tikra paklaida reikia įvertinti, kuri visos Lietuvos vyrų dalis reguliariai užsiima aktyvia fizine veikla);
statistinių hipotezių tikrinimas (pvz., iš tyrimo duomenų reikia nuspręsti, kas Vilniaus universiteto studentams labiau pakelia nuotaiką: plytelė šokolado ar 15 minučių bėgimo).

Šiame skyriuje panagrinėsime kelis žinomus teorinius skirstinius, kurie gali būti naudojami tikimybiškai aprašyti tam tikrų bandymų rezultatus.

6.5 Diskretieji skirstiniai

Diskrečiaisiais skirstiniais vadinami skirstiniai, kurie aprašo diskrečiuosius atsitiktinius dydžius. Šio tipo skirstinių pavyzdžiai:

binominis;
Puasono (Poisson);
neigiamas binominis ir jo specialieji atvejai: Paskalio (Pascal), geometrinis ir Polija (Polya) skirstiniai;
hipergeometrinis skirstinys.

Kai kuriuos iš jų aptarsime plačiau.

6.5.1 Binominis skirstinys

Keletas terminų, susijusių su diskrečiaisiais skirstiniais: sėkmė (arba sėkmingas bandymas) – toks rezultatas, kai įvyko mus dominantis/mums palankus įvykis; nesėkmė (arba nesėkmingas bandymas) – toks rezultatas, kai neįvyko mus dominantis/mums palankus įvykis.

Sakykime, kad vykdome bandymą tokiomis sąlygomis:

atliekant bandymą galimos tik 2 baigtys, pvz., pavyko / nepavyko, sėkmė / nesėkmė, vyras / moteris, sudygo / nesudygo, skaičius / herbas;
bandymus kartojame $n$ kartų $(n = ~1, ~2, ~3, ~...)$: pvz., iš viso yra $n$ objektų, gali įvykti $n$ įvykių ir pan.
vieno bandymo sėkmės tikimybė yra žinoma ir lygi $p$ $(0<p<1)$;
tikimybė $p$ yra pastovi visų bandymų metu;
kiekvieno bandymo rezultatai yra tarpusavyje nepriklausomi.

Tokiu atveju ats.d. $X$ – sėkmingų bandymų skaičius iš $n$ galimų – bus diskretusis $(k = 0,~ 1,~ 2,~ ... ,~ n)$, pasiskirstęs pagal binominį dėsnį ir žymimas:

\[\begin{equation} X \sim \mathcal{B}(n, ~ p) \tag{6.11} \end{equation}\]

Konkrečios reikšmės įgijimo tikimybė aprašoma lygtimi:

\[\begin{equation} P(X = k) = \binom{n}{k}p^kq^{n-k} \tag{6.12} \end{equation}\]

Čia $q = (1-p)$, o $\binom{n}{k} = \frac{n!}{k!(n-k)!}$ – binominis koeficientas. Apie jį plačiau rašoma skyriuje „6.3.3 Klasikinės tikimybės taikymas uždaviniams spręsti“.

Matematinės binominio ats.d. savybės (vidurkis ir dispersija):

\[\begin{equation} \mathbf{E}X = np, ~~~ \mathbf{D}X = npq \tag{6.13} \end{equation}\]

Biologinis pavyzdys: ats.d. – sudygusių sėklų skaičius, kai pasėjame 20.

Jei $X$ yra binominis ats.d., įprastai skirstinio parametrą $n$ žinome (arba numanome) – nes žinome, kiek kartų atliktas eksperimentas. Mums dažniausiai reikia nustatyti sėkmės tikimybę $p$.

Atkreipkite dėmesį, kad binominio skirstinio parametras $n$ nėra tas pats, kas imties dydis, kuris dažnai statistikoje žymimas ta pačia raide. Šio žymėjimo nekeičiau, nes jis plačiai paplitęs ir naudojamas programose, kuriomis atliksime skaičiavimus. Jei gerai išstudijuosite binominį modelį, sunkumų neturėtų kilti.

6.5.2 Puasono skirstinys

Sakykime, kad vykdome bandymą tokiomis sąlygomis:

atliekant bandymą skaičiuojami įvykiai, tenkantys vienam vienetui: objektui arba laiko, ilgio, ploto, erdvės ar kitokiam vienetui;
vidutinis įvykių skaičius $(\lambda)$, tenkantis šiam vienetui, yra žinomas;
maksimalus galimas įvykių skaičius nėra apribotas;
tikimybė, kad įvyks įvykis, ir vidutinis įvykių skaičius yra pastovūs ir nekinta;
įvykiai tarpusavyje yra nepriklausomi.

Tokiu atveju ats.d. $X$ – įvykių skaičius, tenkantis objektui, laiko, erdvės ar kitokiam vienetui – yra diskretusis $(k = 0,~ 1,~ 2,~ ... )$, skirstosi pagal Puasono modelį ir žymimas:

\[\begin{equation} X \sim \mathcal{P}(\lambda) \tag{6.14} \end{equation}\]

Konkrečios reikšmės įgijimo tikimybė aprašoma lygtimi:

\[\begin{equation} P(X = k) = \frac{ \lambda^k }{k!}e^{-\lambda} \tag{6.15} \end{equation}\]

Puasono ats.d. savybės (vidurkis ir dispersija):

\[\begin{equation} \mathbf{E}X = \lambda, ~~~ \mathbf{D}X = \lambda \tag{6.16} \end{equation}\]

Parametras $\lambda$ yra kartu ir vidurkis, ir dispersija. Šis parametras yra tolydusis, o ne diskretusis (t.y., nebūtinai sveikasis skaičius).

Puasono skirstinys dar vadinamas retų įvykių skirstiniu, nes įprastai juo modeliuojami retai įvykstantys reiškiniai.

Biologiniai pavyzdžiai:

ats.d. – mutacijų, įvykstančių vienoje chromosomoje, skaičius.
ats.d. – retos ligos atvejų, įvykstančių populiacijoje per vienerius metus, skaičius.

6.5.3 Binominio skirstinio aproksimacija Puasono skirstiniu

Sakykime, kad savo tyrimo rezultatą galime aprašyti binominio skirstinio modeliu $X \sim \mathcal{B}(n, ~ p)$, tačiau $n$ palyginus su $p$ – labai didelis (tarkime, $n > 1000$), o $p$ – labai mažas (tarkime, $p<0{,}001$). Tokiu atveju binominio skirstinio tikimybes pakankamai gerai atitinka Puasono skirstinio $\mathcal{P}(np)$ tikimybės: teorinį binominio skirstinio vidurkį prilyginame teoriniam Puasono skirstinio vidurkiui $(np \sim \lambda)$ ir skaičiavimus atliekame naudodami Puasono skirstinį.

Įprastai šitokios aproksimacijos reikia, jei skaičiavimus atliekame ne kompiuteriu arba grafinės skaičiuoklės, tokios kaip „GeoGebra“, užstringa dėl didelių skaičių. Skaičiuojant programa „R“ problemų įprastai nekyla.

6.5.4 Geometrinis skirstinys

Potemė apie geometrinį skirstinį į kursą neįtraukta.
Pereikite prie potemės „Tolydieji skirstiniai“.

Sakykime, kad vykdome bandymą tokiomis sąlygomis:

atliekant bandymą galimos tik 2 baigtys, pvz., pavyks / nepavyks, vyras / moteris;
bandymus kartojame tol, kol sulaukiame pirmos sėkmės;
vieno bandymo sėkmės tikimybė yra žinoma ir lygi $p$ $(0<p<1)$;
tikimybė $p$ yra pastovi visų bandymų metu;
kiekvieno bandymo rezultatai yra tarpusavyje nepriklausomi.

Tada ats.d. $X$ galime apsibrėžti kaip nesėkmingų bandymų skaičių iki pirmos sėkmės (į $X$ sėkmingų bandymų skaičius nėra įskaitytas). Toks ats.d. $X$ yra diskretusis $(k = 0,~ 1,~ 2,~ …)$, skirstosi pagal geometrinį skirstinį ir žymimas:

\[\begin{equation} X \sim \mathcal{Geom}(p) \tag{6.17} \end{equation}\]

Konkrečios reikšmės įgijimo tikimybė aprašoma lygtimi:

\[\begin{equation} P(X = k) = pq^k \tag{6.18} \end{equation}\]

Čia $q =(1-p)$.

Geometrinio ats.d. savybės (vidurkis ir dispersija):

\[\begin{equation} \mathbf{E}X = \frac{q}{p}, ~~~ \mathbf{D}X = \frac{q}{p^2} \tag{6.19} \end{equation}\]

Biologinis pavyzdys: ats.d. yra gimusių berniukų skaičius prieš gimstant pirmai mergaitei.

Pastaba. Geometrinis skirstinys turi du susijusius, bet skirtingus matematinius apibrėžimus. Šiame skyriuje pasirinktas tas, kuris naudojamas programose R ir GeoGebra.

Čekanavičiaus ir Murausko vadovėlyje pateiktas kitas matematinis geometrinio skirstinio apibrėžimas, tad formulės neatitinka. Tačiau rezultatus galime persiskaičiuoti. Pavyzdžiui, jei norime modeliuoti, kiek įvykių įvyko iš viso $($pažymėkime $X^*)$, o žinome, kiek iš jų buvo nesėkmingi $(X)$, prie gautos konkrečios $X$ reikšmės pridedame 1 (sėkmingų įvykių skaičių): $k^* = k + 1$ ($k^*$ – įvykių skaičius iš viso). Analogiškai ir prie vidurkio pridedame 1: $\mathbf{E}X^* = \mathbf{E}X + 1$. Tačiau prie dispersijos nieko pridėti nereikia, nes prie kiekvienos reikšmės pridėta konstanta dispersijos nepakeičia: $\mathbf{D}X^* = \mathbf{D}X$. Jei dėl geometrinių atsitiktinių dydžių kyla klausimų ar neaiškumų, siūlau peržvelgti šį šaltinį (nuoroda ), kuriame aprašomi skirtumai.

6.5.5 Neigiamas binominis skirstinys

Potemė apie neigiamą binominį skirstinį į kursą neįtraukta.
Pereikite prie potemės „Tolydieji skirstiniai“.

Sakykime, kad vykdome bandymą tokiomis sąlygomis:

atliekant bandymą galimos tik 2 baigtys, pvz., pavyks / nepavyks;
bandymus kartojame tol, kol sulaukiame $r$ sėkmių $(r > 0)$;
vieno bandymo sėkmės tikimybė yra žinoma ir lygi $p$ $(0<p<1)$;
tikimybė $p$ yra pastovi visų bandymų metu;
kiekvieno bandymo rezultatai yra tarpusavyje nepriklausomi.

Tada ats.d. $X$ galime apsibrėžti kaip nesėkmingų bandymų skaičių iki $r$-tosios sėkmės (į $X$ sėkmingų bandymų skaičius nėra įskaitytas). Toks ats.d. $X$ yra diskretusis $(k = 0,~ 1,~ 2,~ …)$, skirstosi pagal neigiamą binominį skirstinį ir žymimas:

\[\begin{equation} X \sim \mathcal{NB}(r, p) \tag{6.20} \end{equation}\]

Konkrečios reikšmės įgijimo tikimybė aprašoma lygtimi:

\[\begin{equation} P(X = k) = \binom{k+r-1}{r-1}p^r q^k \tag{6.21} \end{equation}\]

Čia $q =(1-p)$.

Neigiamo binominio ats.d. savybės (vidurkis ir dispersija):

\[\begin{equation} \mathbf{E}X = \frac{qr}{p}, ~~~ \mathbf{D}X = \frac{qr}{p^2} \tag{6.22} \end{equation}\]

Biologinis pavyzdys: ats.d. yra gimusių berniukų skaičius prieš gimstant penktai mergaitei.

Bendruoju atveju parametras $r$ gali nebūti sveikasis skaičius. Kai jis yra sveikasis, neigiamas binominis skirstinys dar vadinamas Paskalio (Pascal) skirstiniu (t.y., tam tikras neigiamo binominio skirstinio atvejis). Geometrinis skirstinys – taip pat atskiras neigiamo binominio ir Paskalio skirstinių atvejis, kai $r = 1$.

\[\begin{equation} X \sim \mathcal{NB}(r = 1,~ p) = Geom(p) \tag{6.23} \end{equation}\]

Paskalio skirstinys – tai neigiamas binominis skirstinys, kai parametras $r$ yra sveikasis skaičius.

Geometrinis skirstinys – tai neigiamas binominis skirstinys, kai parametras $r = 1$.

Pastaba. Neigiamas binominis skirstinys turi keletą skirtingų matematinių formuluočių, o šiame skyriuje aprašyta ta, kuri naudojama programose R ir GeoGebra. Norėdami modeliuoti kitaip apibrėžtą atsitiktinį dydį, rezultatus galime persiskaičiuoti. Pavyzdžiui, jei norime modeliuoti, kiek įvykių įvyko iš viso $($pažymėkime $X^*)$, o žinome, kiek iš jų buvo nesėkmingi $(X)$, prie gautos konkrečios $X$ reikšmės pridedame sėkmingų įvykių skaičių $r$: $k^* = k + r$ ($k^*$ – įvykių skaičius iš viso). Analogiškai ir prie vidurkio pridedame $r$: $\mathbf{E}X^* = \mathbf{E}X + r$. Tačiau prie dispersijos nieko pridėti nereikia, nes prie kiekvienos reikšmės pridėta konstanta dispersijos nepakeičia: $\mathbf{D}X^* = \mathbf{D}X$. Jei kils neaiškumų dėl neigiamo binominio skirstinio apibrėžimų, siūlau peržiūrėti šį šaltinį (nuoroda ).

6.6 Tolydieji skirstiniai

Tolydžiaisiais skirstiniais vadinami skirstiniai, kurie aprašo tolydžiuosius atsitiktinius dydžius. Šio tipo skirstinių pavyzdžiai:

normalusis (Gauso) skirstinys;
log-normalusis skirstinys;
tolygusis skirstinys;
Lorenco/Koši (Lorentz/Cauchy) skirstinys;
Stjudento⁵ $t$ skirstinys;
Fišerio $F$ skirstinys;
$\chi^2$ (chi kvadratu) skirstinys.

Kai kuriuos iš jų aptarsime plačiau.

6.6.1 Normalusis skirstinys

Normalusis skirstinys yra tolydusis. Tikimybių teorijoje tai pats svarbiausias skirstinys, nes juo galima aprašyti daugelį natūraliai vykstančių reiškinių. Atsitiktinis dydis $X$, kuris skirstosi pagal normalųjį skirstinį, žymimas:

\[\begin{equation} X \sim \mathcal{N}(\mu, \sigma^2) \tag{6.24} \end{equation}\]

Normaliojo atsitiktinio dydžio tikimybės tankis $p(x)$ ties konkrečia reikšme $x$ skaičiuojamas pagal formulę:

\[\begin{equation} p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}~e^{-\frac{(x-\mu)^2}{2\sigma^2}} \tag{6.25} \end{equation}\]

Parametrai:

$\mu$ – vidurkis $(\mu \in \mathbb{R})$;
$\sigma^2$ – dispersija $(\sigma^2 > 0)$. Pastaba: paprastumo dėlei statistinės programos ir tikimybių skaičiuoklės vietoje dispersijos dažnai naudoja standartinį nuokrypį. Tačiau teorinėje statistikoje (ir uždavinių formuluotėse), jei nepasakyta kitaip, užrašoma dispersija.

Normaliojo ats.d. savybės (vidurkis, dispersija ir standartinis nuokrypis):

\[\begin{equation} \mathbf{E}X = \mu, ~~~ \mathbf{D}X = \sigma^2, ~~~ \sqrt{\mathbf{D}X} = \sigma \tag{6.26} \end{equation}\]

Standartinis normalusis:

\[\begin{equation} X \sim \mathcal{N}(0; 1) \tag{6.27} \end{equation}\]

Standartinio normaliojo skirstinio (dar vadinamo $z$ skirstiniu) savybės – vidurkis lygus nuliui, dispersija ir standartinis nuokrypis lygūs vienetui:

\[\begin{equation} \mathbf{E}X = 0, ~~~ \mathbf{D}X = 1, ~~~ \sqrt{\mathbf{D}X} = 1 \tag{6.28} \end{equation}\]

Jei skirstinys normalusis, galioja empirinės taisyklės (grafinė iliustracija: nuoroda ).

6.6.2 Log-normalusis skirstinys

Jei atsitiktinis dydis gali įgyti tik teigiamas reikšmes $(X>0)$, o atlikus logaritminę transformaciją jo skirstinys tampa normalusis, tada sakoma, kad atsitiktinis dydis $X$ pasiskirstęs pagal log-normalųjį skirstinį:

\[\begin{equation} log(X) \sim \mathcal{N}(\mu, \sigma^2) \tag{6.29} \end{equation}\]

Atlikę logaritminę transformaciją, su šiuo dydžiu galime elgtis kaip su įprastu normaliuoju.

Informacijos šaltiniai

Čekanavičius V., Murauskas G. Statistika ir jos taikymai I. Vilnius: TEV (2006).

Venclovienė J. Statistiniai metodai medicinoje. Kaunas: Vytauto didžiojo universitetas (2010). Prieiga per internetą: https://www.vdu.lt/cris/bitstream/20.500.12259/271/1/ISBN9789955125587.pdf.

Angl. permutations (without repetition).↩︎
Angl. ordered arrangement↩︎
Angl. combination.↩︎
Anglų statistikas William Sealy Gosset (1876 – 1937) slapyvardžiu Stjudentas.↩︎