5. Grafikai

Grafinė analizė – neatsiejama statistinės analizės dalis: prieš pradedant sudėtingesnę analizę, būtina duomenis nusibraižyti. Akimis mes priimame didelę dalį informacijos, todėl grafikai ir diagramos padės pastebėti esminius duomenų bruožus.

Grafikai ir diagramos padeda greitai pastebėti esminius duomenų bruožus.

Aišku, tam, kad grafinė analizė apskritai būtų naudinga, turime mokėti suprasti ir analizuoti įvairius statistinius grafikus. Šioje dalyje pateikta teorinė medžiaga apie dažnai statistinėms suvestinėms atlikti naudojamus grafikus. Peržiūrėkite pateiktą video medžiagą, išnagrinėkite grafikus.

Vos įsikėlę duomenis analizei, peržiūrėkite juos grafiškai.

Skyrius apie aprašomąją statistiką ir statistinius grafikus galite rasti vadovėliuose (Čekanavičius ir Murauskas 2006; Venclovienė 2010; Field ir kt. 2012).

5.1 Grafikai vieno kintamojo apibendrinimui

5.1.1 Kategoriniams duomenims

Kategoriniams duomenims apibendrinti įprastai naudojama stulpelinė diagrama (pav. 5.1).

Šis grafikas tinkamas nominaliesiems, ranginiams ir kiekybiniams diskretiesiems duomenims, kai skirtingų reikšmių yra nedaug.

Apie šio tipo grafiką pasakojama video epizode 5.1.

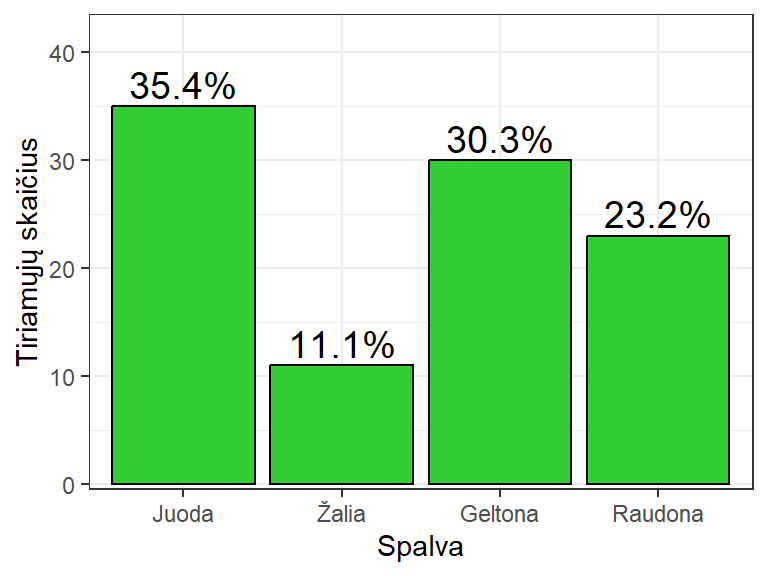
Stulpelinė diagrama yra skirta kategoriniams/diskretiesiems duomenims atvaizduoti.

Pav. 5.1: Stulpelinė diagrama yra skirta kategoriniams/diskretiesiems duomenims atvaizduoti.

Video epizodas 5.1 Stulpelinė diagrama.


5.1.2 Tolydiesiems duomenims

Tolydiesiems (bendruoju atveju – kiekybiniams) duomenims atvaizduoti įprastai naudojami tokie grafikai, kaip histograma, branduolinio tankio ar stačiakampė diagramos.

Šiame poskyryje aptariami grafikai tinkami ir kiekybiniams tolydiesiems, ir kiekybiniams diskretiesiems duomenims.

Video epizodas 5.2 Histograma.


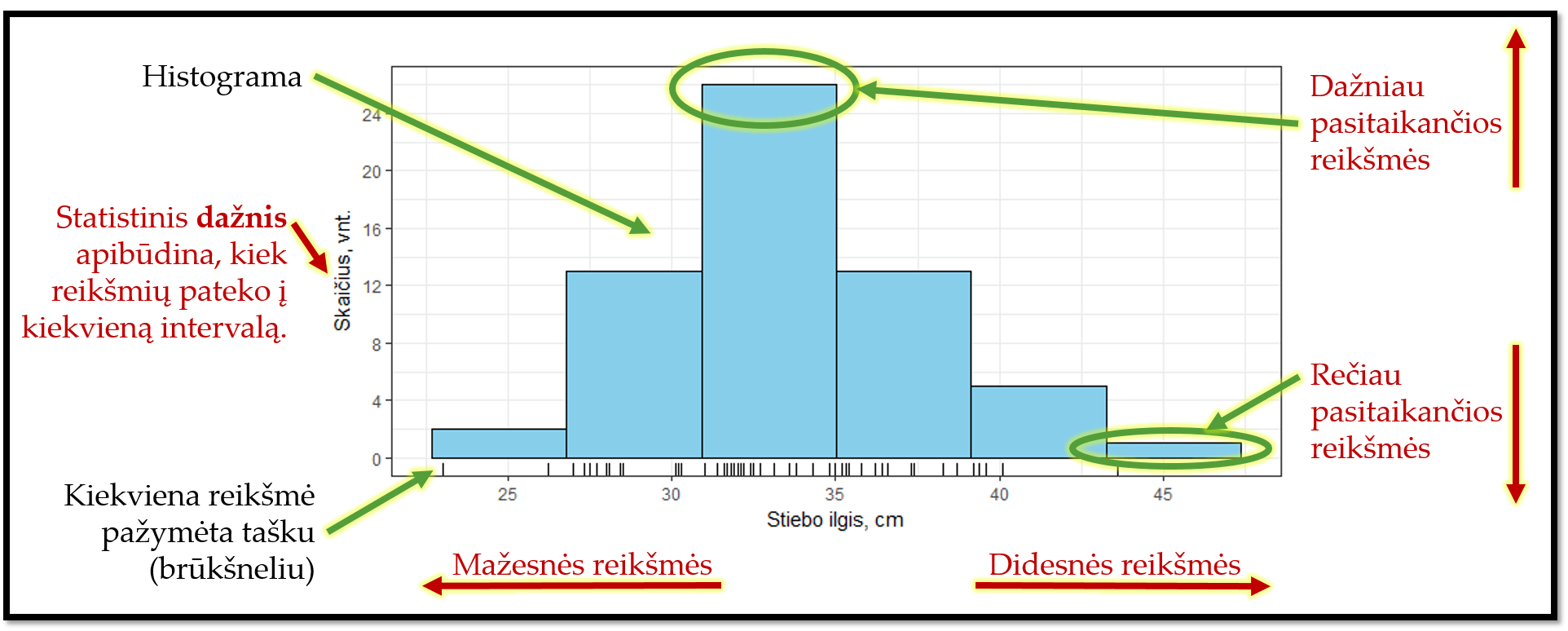
Pavyzdys, kaip analizuoti histogramą.

Pav. 5.2: Pavyzdys, kaip analizuoti histogramą.

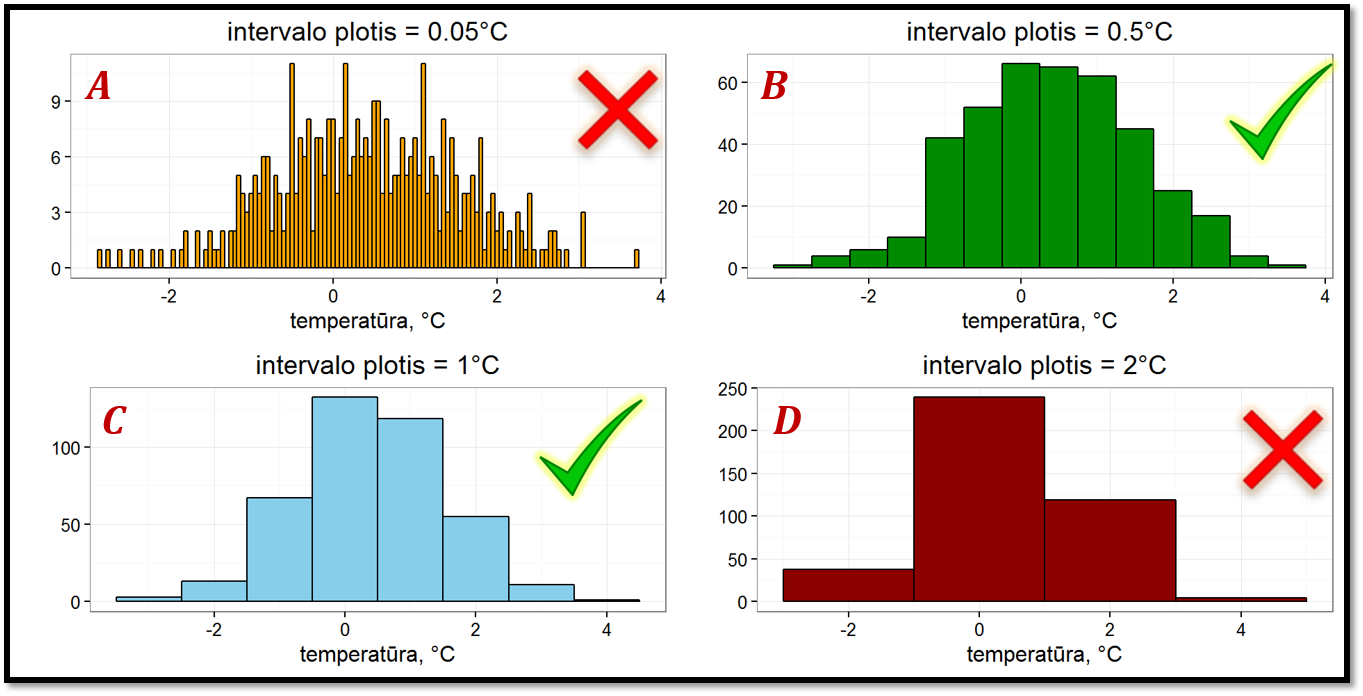
Histogramos grupavimo intervalo pločio parinkimas. A -- per siauras intervalas (per didelis intervalų skaičius) išryškina triukšmą ir paslepia tendenciją. D -- per platūs intervalai (per mažas intervalų skaičius) taip pat paslepia tikrąją tendenciją. B, C -- tinkamai parinktas intervalų skaičius, matoma tendencija. B -- geriausias variantas. Įprastai reikia tarp 5 ir 15 intervalų.

Pav. 5.3: Histogramos grupavimo intervalo pločio parinkimas. A – per siauras intervalas (per didelis intervalų skaičius) išryškina triukšmą ir paslepia tendenciją. D – per platūs intervalai (per mažas intervalų skaičius) taip pat paslepia tikrąją tendenciją. B, C – tinkamai parinktas intervalų skaičius, matoma tendencija. B – geriausias variantas. Įprastai reikia tarp 5 ir 15 intervalų.


Video epizodas 5.3 Branduolinio tankio diagrama.


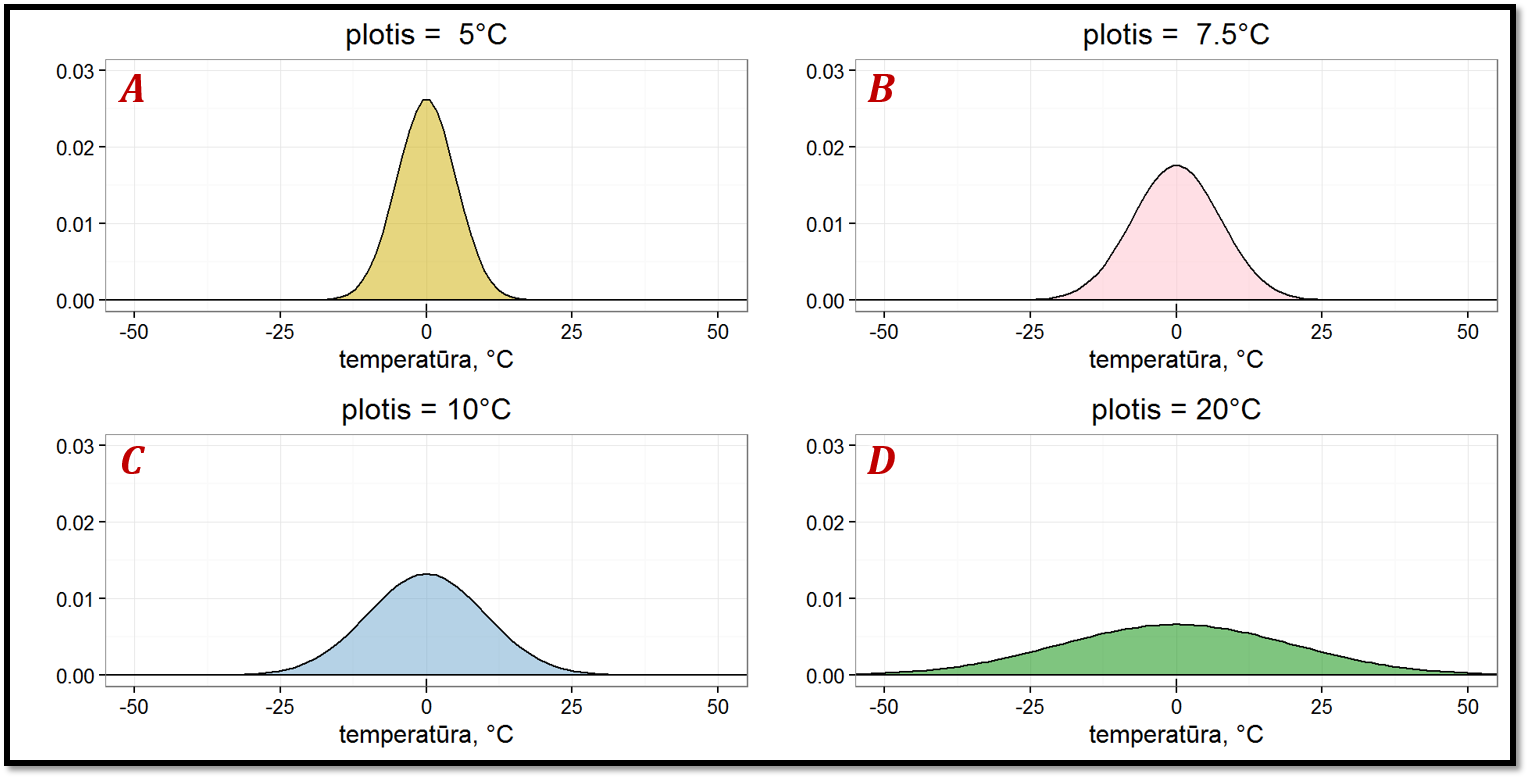
Vienas duomenų taškas atvaizduotas branduoline kreive. Branduolinio tankio diagramoje vienas taškas aprašomas kreive, vadinama branduoliu, kuri ties centru aukščiausia, o į kraštus mažėja. Pavyzdyje (A, B, C, D) tai Gauso kreivės, kurios gali skirtis savo pločiu. Branduolio formą ir plotį pasirenka tyrėjas, visgi kiekvienam grafiko taškui aprašyti naudojami identiški branduoliai.

Pav. 5.4: Vienas duomenų taškas atvaizduotas branduoline kreive. Branduolinio tankio diagramoje vienas taškas aprašomas kreive, vadinama branduoliu, kuri ties centru aukščiausia, o į kraštus mažėja. Pavyzdyje (A, B, C, D) tai Gauso kreivės, kurios gali skirtis savo pločiu. Branduolio formą ir plotį pasirenka tyrėjas, visgi kiekvienam grafiko taškui aprašyti naudojami identiški branduoliai.

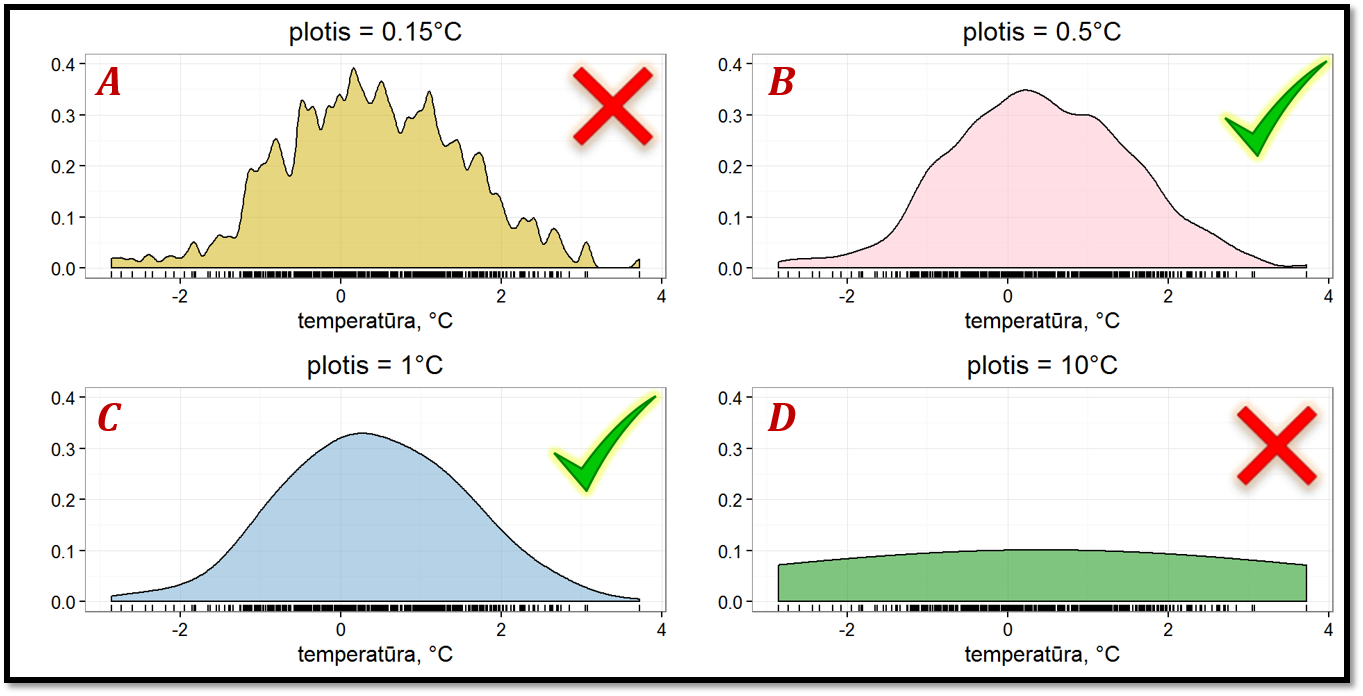
Branduolinio tankio diagramoje (BTD) atvaizduoti visi duomenų eilutės taškai. Svarbu pasirinkti tinkamą branduolio plotį. A -- per siauri branduoliai nepakankamai gerai suglotnina kreivę, matosi triukšmas, sunku įžiūrėti tendenciją. D -- per platūs branduoliai per daug suglotnina duomenis, BTD smarkiai išeina už realių duomenų ribų, taip pat nesimato tikrosios tendencijos. B, C -- pakankamai gerai parinktas branduolio plotis. C -- geriausias variantas.

Pav. 5.5: Branduolinio tankio diagramoje (BTD) atvaizduoti visi duomenų eilutės taškai. Svarbu pasirinkti tinkamą branduolio plotį. A – per siauri branduoliai nepakankamai gerai suglotnina kreivę, matosi triukšmas, sunku įžiūrėti tendenciją. D – per platūs branduoliai per daug suglotnina duomenis, BTD smarkiai išeina už realių duomenų ribų, taip pat nesimato tikrosios tendencijos. B, C – pakankamai gerai parinktas branduolio plotis. C – geriausias variantas.

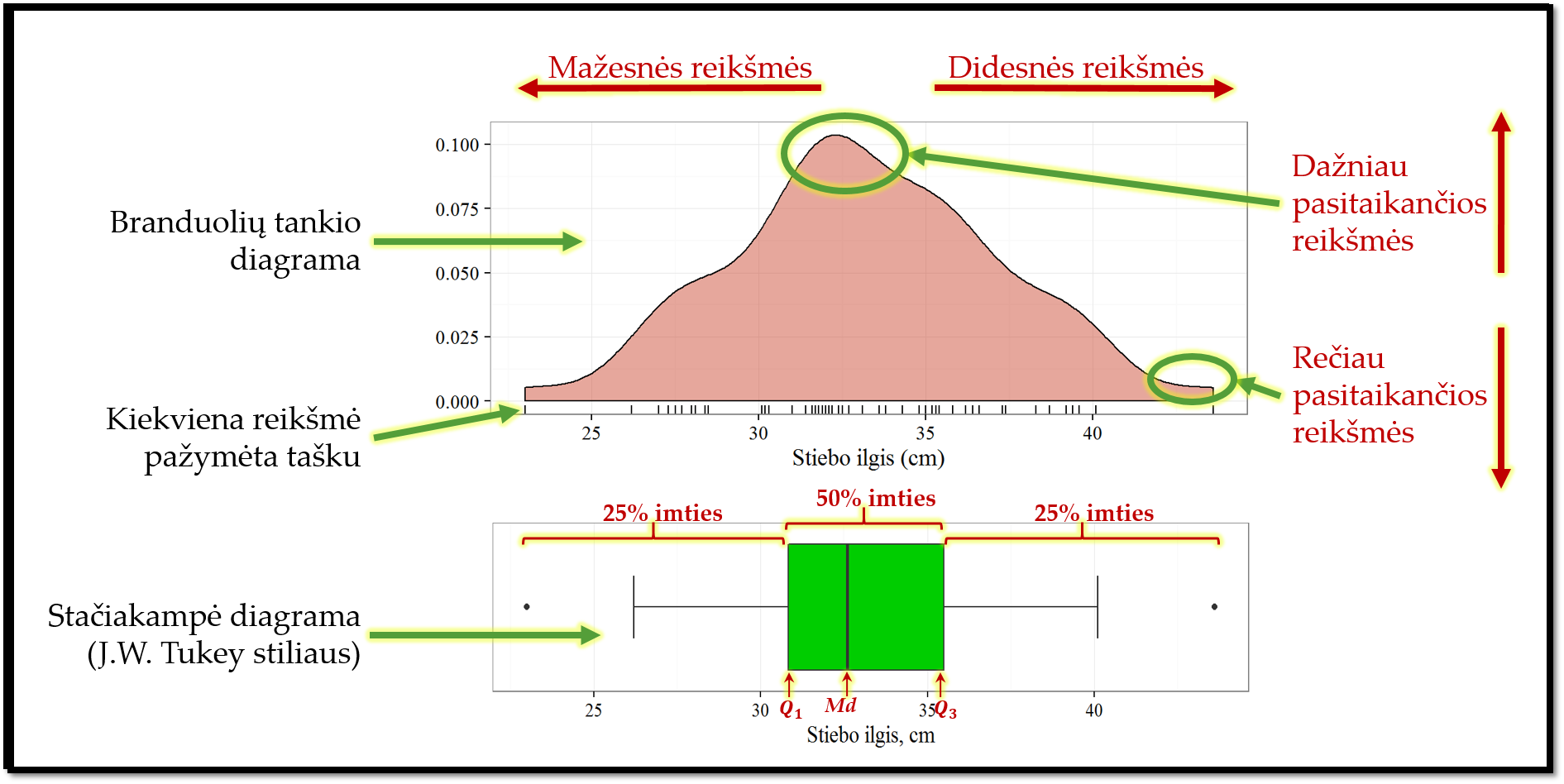
Informacijos branduolinio tankio (BTD) ir stačiakampėje diagramoje palyginimas. Abiejų tipų diagramose atvaizduoti tie patys duomenys. $Md$ -- mediana, $Q_1$, $Q_3$ -- pirmasis ir trečiasis kvartiliai.

Pav. 5.6: Informacijos branduolinio tankio (BTD) ir stačiakampėje diagramoje palyginimas. Abiejų tipų diagramose atvaizduoti tie patys duomenys. \(Md\) – mediana, \(Q_1\), \(Q_3\) – pirmasis ir trečiasis kvartiliai.

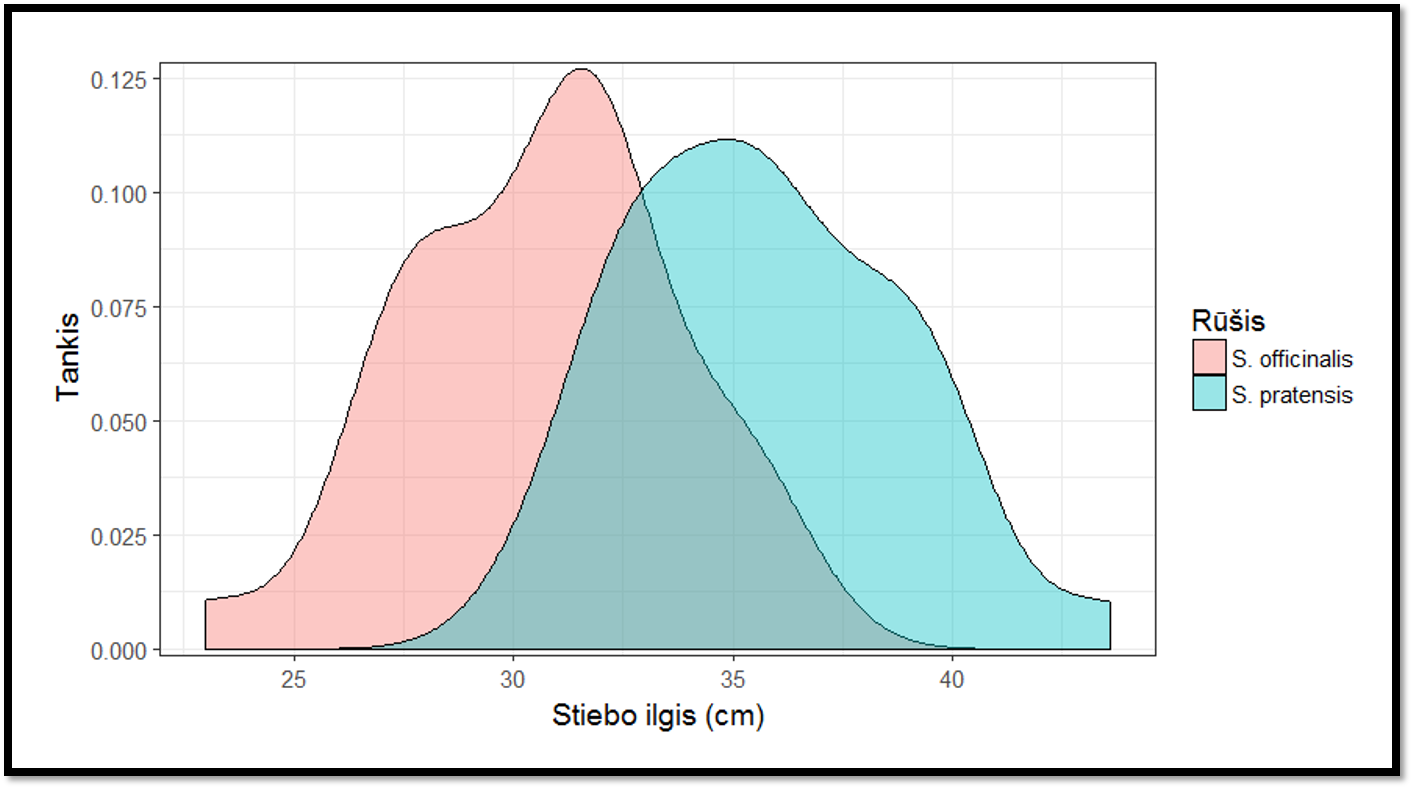
Branduolinio tankio diagramos (BTD) naudojimas grupių lyginimui. Iš grafiko matosi, kad *S. pratensis* augalai turėjo santykinai daugiau ilgesnių stiebų nei *S. officinalis* (nes mėlynas grafikas pasislinkęs į didesnių reikšmių pusę).

Pav. 5.7: Branduolinio tankio diagramos (BTD) naudojimas grupių lyginimui. Iš grafiko matosi, kad S. pratensis augalai turėjo santykinai daugiau ilgesnių stiebų nei S. officinalis (nes mėlynas grafikas pasislinkęs į didesnių reikšmių pusę).


Video epizodas 5.3 Branduolinio tankio diagrama.


Straipsnyje „Boxplots“ pasakojama apie tai, ką reiktų matyti ir kaip interpretuoti stačiakampes diagramas.


Video epizodas 5.4 Stačiakampė, smuikinė ir pasklaidytų taškų diagramos.


5.1.3 Diagramų palyginimas

Grafiniam informacijos palyginimui, pateiktam šio poskyrio grafikuose 5.8, 5.9, 5.11, buvo dirbtinai sugeneruoti duomenys. Kintamasis „Reikšmė“ padalintas į 8 duomenų grupes (nuo A iki H). Grupė A yra kontrolinė. Visos kitos nuo jos skiriasi pagal vieną konkretų požymį:

  1. imties dydį (n): A grupėje n = 250 (didesnė grupė), B – n = 63 (keturis kartus mažesnė grupė);
  2. centro padėtį: A vidurkis yra 50 (vidutiniškai didesnės reikšmės), C – 40 (vidutiniškai mažesnės reikšmės);
  3. sklaidą: A standartinis nuokrypis (SD) yra 5 (mažesnė sklaida), D – 10 (didesnė sklaida);
  4. viršūnių skaičių: A viena viršūnė, E – dvi viršūnės;
  5. simetriją: A pasiskirstymas simetriškas, F – dešinioji asimetrija (skirstinio „uodega“ nutįsusi į didelių reikšmių pusę);
  6. simetriją: A pasiskirstymas simetriškas, G – kairioji asimetrija (skirstinio „uodega“ nutįsusi į mažų reikšmių pusę);
  7. išskirtis: A ryškių išskirčių nėra, H – yra du labai smarkiai nuo centro nutolę taškai.

Peržvelkite žemiau pateiktus grafikus ir įvertinkite, kaip ši informacija juose matoma.

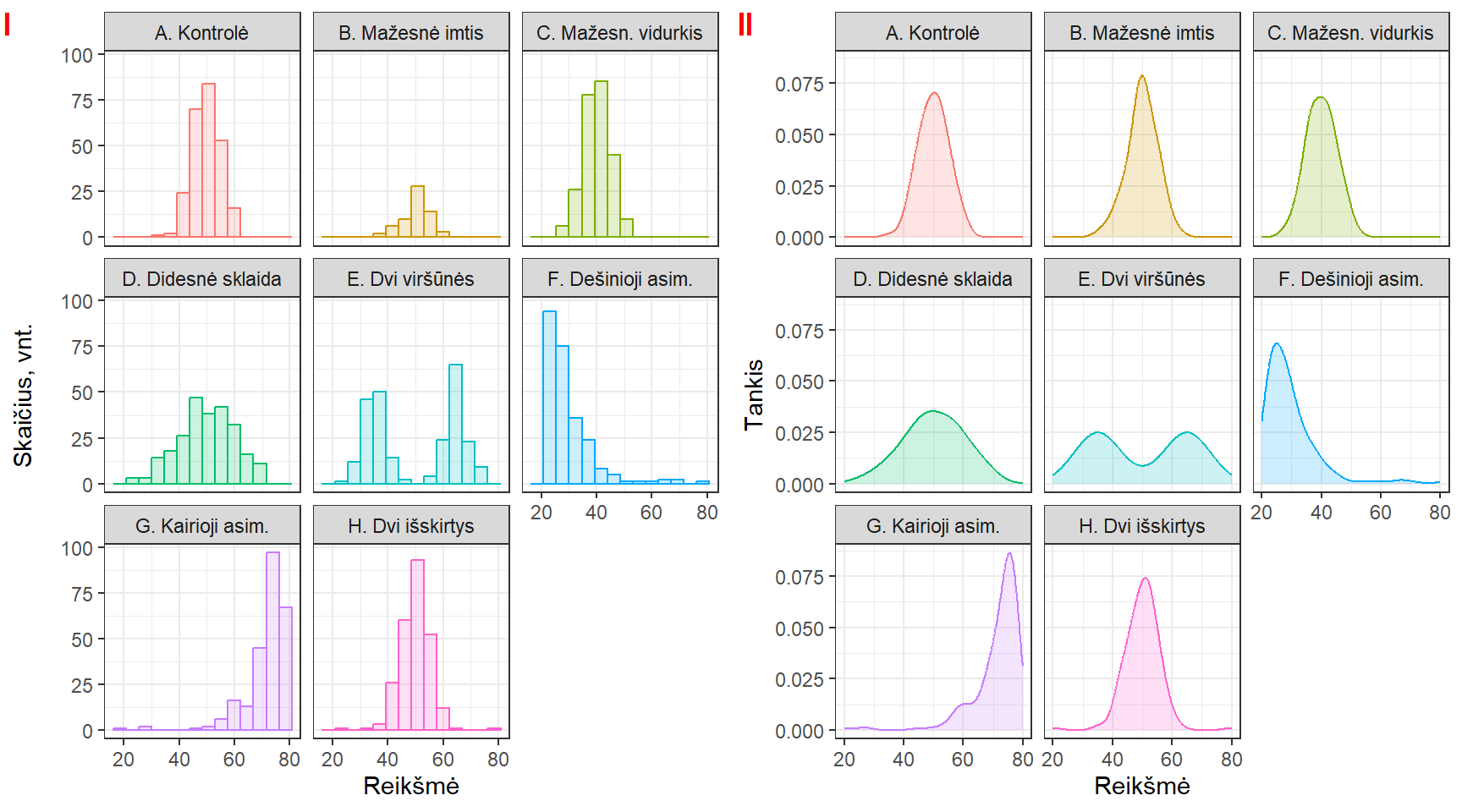
Grupių palyginimas duomenis atvaizduojant (I) **histograma** ir (II) **branduolinio tankio diagrama** (BTD). Histogramoje matomas imties dydis, tačiau jei reiktų sudėti kelis grafikus viename lange, vaizdesnė būtų BTD (pvz., pav. \@ref(fig:03-plots-density-4)).

Pav. 5.8: Grupių palyginimas duomenis atvaizduojant (I) histograma ir (II) branduolinio tankio diagrama (BTD). Histogramoje matomas imties dydis, tačiau jei reiktų sudėti kelis grafikus viename lange, vaizdesnė būtų BTD (pvz., pav. 5.7).

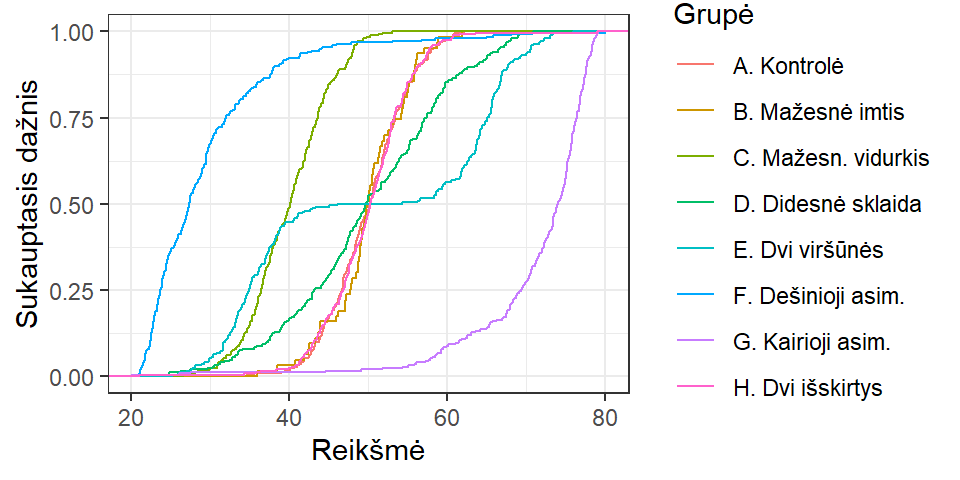
Empirinio sukauptojo santykinio dažnio diagrama (ECDF): palyginimas viename grafike.

Pav. 5.9: Empirinio sukauptojo santykinio dažnio diagrama (ECDF): palyginimas viename grafike.

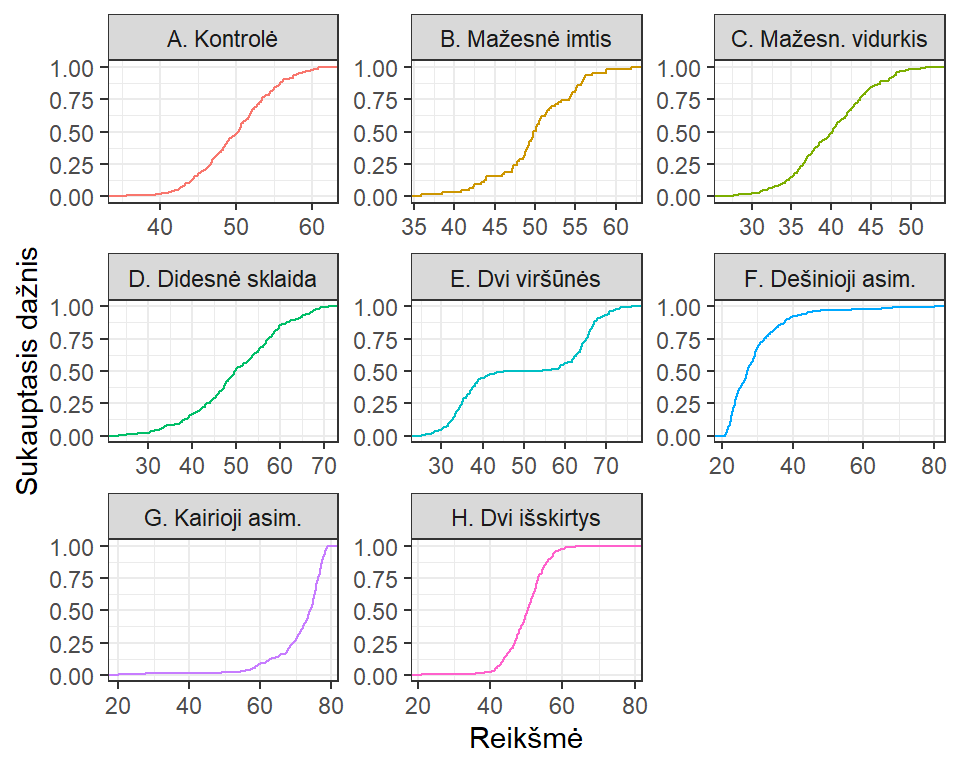
Empirinio sukauptojo santykinio dažnio diagrama (ECDF): grafiko formos palyginimas (x ašies ribos grafikuose skiriasi).

Pav. 5.10: Empirinio sukauptojo santykinio dažnio diagrama (ECDF): grafiko formos palyginimas (x ašies ribos grafikuose skiriasi).

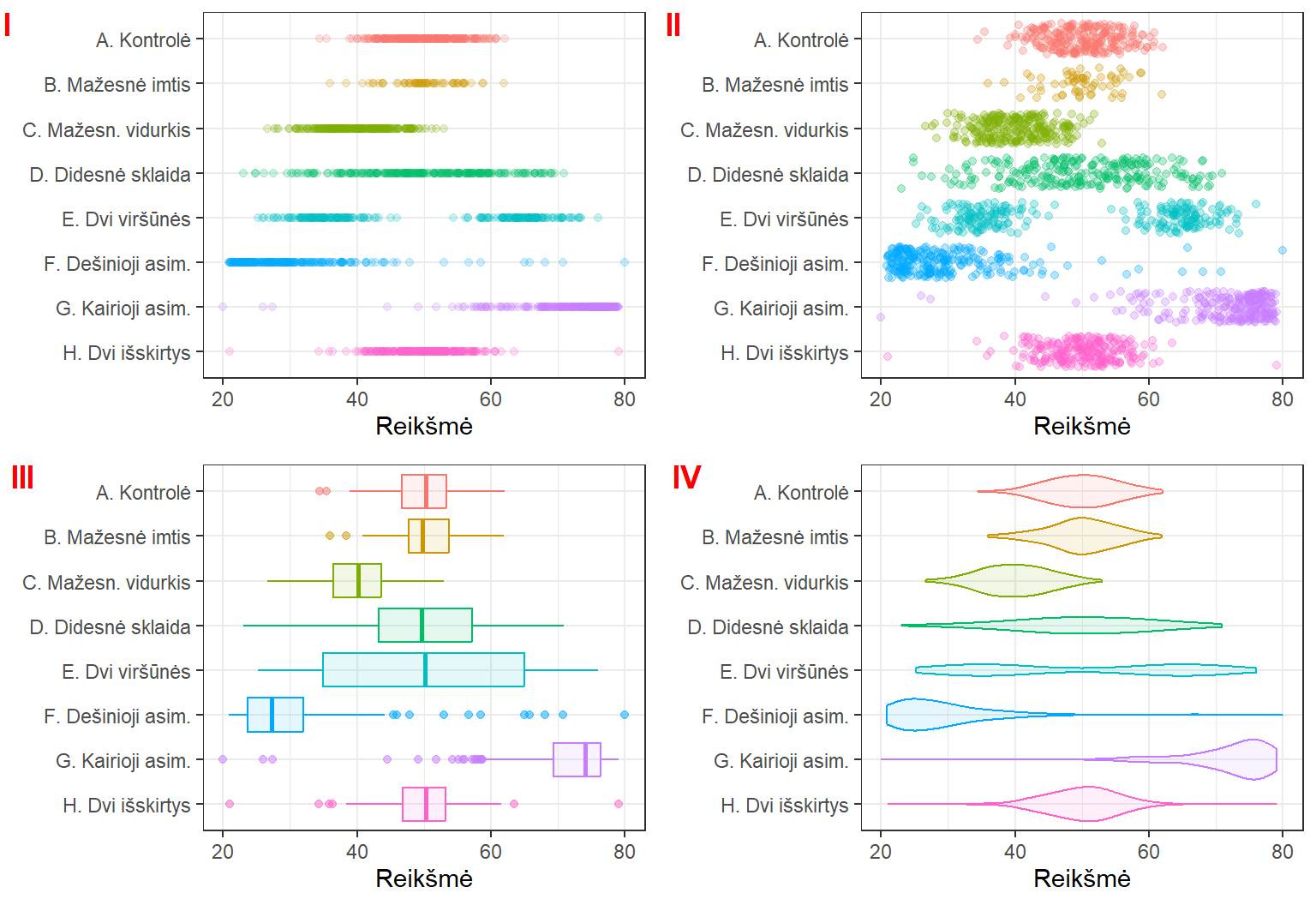
Grupių palyginimas duomenis atvaizduojant (I) **taškais**, (II) **pasklaidytų taškų diagrama**, (III) **stačiakampe diagrama** bei (IV) **smuikine diagrama**. (I) Visi taškai išsidėstę į vieną liniją. Kai taškai persidengia, grafikas tampa mažai informatyvus. Papildomos informacijos gali suteikti taškų permatomumas: jei taškų vienoje vietoje daug, spalva tampa ryškesnė. (II) Siekiant išvengti persidengimo, taškai pasklaidyti x ašiai lygiagrečia kryptimi. (III) Grafikas vaizduoja skaitines suvestines. Klasikiniame grafiko variante gali būti matoma asimetrija, bet nesimato imties dydžio ir viršūnių skaičiaus. (IV) Šis grafikas -- tai stačiakampės ir branduolinio tankio diagramų hibridas.

Pav. 5.11: Grupių palyginimas duomenis atvaizduojant (I) taškais, (II) pasklaidytų taškų diagrama, (III) stačiakampe diagrama bei (IV) smuikine diagrama. (I) Visi taškai išsidėstę į vieną liniją. Kai taškai persidengia, grafikas tampa mažai informatyvus. Papildomos informacijos gali suteikti taškų permatomumas: jei taškų vienoje vietoje daug, spalva tampa ryškesnė. (II) Siekiant išvengti persidengimo, taškai pasklaidyti x ašiai lygiagrečia kryptimi. (III) Grafikas vaizduoja skaitines suvestines. Klasikiniame grafiko variante gali būti matoma asimetrija, bet nesimato imties dydžio ir viršūnių skaičiaus. (IV) Šis grafikas – tai stačiakampės ir branduolinio tankio diagramų hibridas.

5.2 Kaip analizuoti grafikus?

Analizuodami grafikus atkreipkite dėmesį į duomenų padėtį, sklaidą, pasiskirstymo formą (simetriją/asimetriją, viršūnių skaičių), imties dydį ir išskirtinius bruožus, jei tokių yra. Jei analizuojate duomenis pogrupiais, šiuos dalykus pastebėkite kiekvienai grupei atskirai (žr. poskyrį „5.3.3 Grafinis grupių palyginimas“).

Kiekvienam iš šių bruožų apibūdinti gali padėti OSEM akronimas (metodo autorius – Jeremy Brocklehurst):

  • O (obvious) – tam tikros akivaizdžios grafiko savybės pastebėjimas;
  • S (specify) – patikslinimas ir sukonkretinimas taip, kad suprastų kitas;
  • E (evidence) – pagrindimas skaičiais, papildomos analizės rezultatais;
  • M (meaning) – įprasminimas:
    • „Kas iš to šiame kontekste?“
    • „Kaip tai siejasi su tyrimo klausimu ir problema?“ (Nes tyrimas/analizė prasideda nuo klausimo ar problemos formulavimo.)

Rekomenduojami video resursai: „Analysing and commenting on graphical output using OSEM“ .

5.3 Grafikai kintamųjų porai

Jei turime 2 kintamuosius, dažni šitokie grafikų pasirinkimai:

  • sklaidos diagrama (angl. scatter plot) – jei du kiekybiniai kintamieji;
  • stačiakampė diagrama, histograma, BTD ar panašaus tipo diagrama grupėms – jei skirtingų rūšių kintamieji (t.p. žr. poskyrį „5.3.3 Grafinis grupių palyginimas“);
  • mozaikinė diagrama (angl. mosaic plot, Marimekko diagram) arba stulpelinė diagrama grupėms – jei du kategoriniai, diskretieji, nominalieji kintamieji.

5.3.1 Sklaidos diagrama

Sklaidos diagrama yra grafikas, taškais (simboliais) atvaizduojantis kiekybinių kintamųjų poros pasiskirstymą.

Sklaidos diagramos pavyzdys: sąsaja tarp kačių kūno ir širdies svorio. Duomenų šaltinis [@Fisher1947].

Pav. 5.12: Sklaidos diagramos pavyzdys: sąsaja tarp kačių kūno ir širdies svorio. Duomenų šaltinis (Fisher 1947).

Analizuojant šio tipo grafiką reiktų vertinti:

  1. Ryšio pobūdį:
    • tiesinis,
    • netiesinis (monotoninis arba nemonotoninis),
    • ryšio nėra (pvz., jei sklaidos diagramoje matomas apskritimo formos taškų „debesėlis“ arba tiesė, lygiagreti kuriai nors – x arba y – ašiai).
  2. Ryšio stiprumą:
    • visiška priklausomybė (taškai išsidėstę į vieną kreivę, pvz., tiesę, paklaidų nėra);
    • stiprus (taškai arti įsivaizduojamos geriausiai juos apibūdinančios kreivės, paklaidos mažos);
    • silpnas (taškai toli nuo įsivaizduojamos linijos, paklaidos didelės);
    • ryšio nėra.
  3. Ryšio kryptį:
    • tiesioginis,
    • atvirkštinis,
    • kintamo pobūdžio;
    • (ryšio nėra).
Ryšio vertinimas pagal sklaidos diagramą. Adaptuota iš [„Correlation and dependence“ <i class="fa fa-external-link-alt" aria-hidden="true"></i>](https://en.wikipedia.org/wiki/correlation){target="_blank"} (Denis Boigelot, [CC0](https://creativecommons.org/publicdomain/zero/1.0/deed.en){target="_blank"}).

Pav. 5.13: Ryšio vertinimas pagal sklaidos diagramą. Adaptuota iš „Correlation and dependence“ (Denis Boigelot, CC0).

5.3.2 Kreivių diagrama

Įprastai 2 kintamuosius vaizduojame kreivėmis, kai vieno kintamojo, dažniausiai vaizduojamo x ašyje, reikšmės renkamos natūralia didėjimo tvarka. Įprastai tai būna kokio nors rodiklio kitimas laike (pvz., kondensatoriaus išsikrovimo dinamika), spektroskopinio signalo kitimas pagal bangos ilgį (pvz., hemoglobino sugerties spektras) ar pan.

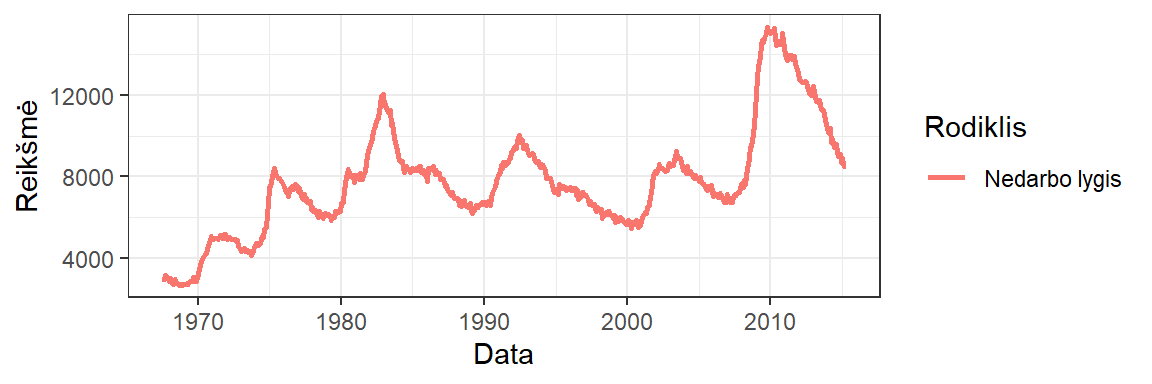
Duomenų, atvaizduotų kreive, pavyzdys.

Pav. 5.14: Duomenų, atvaizduotų kreive, pavyzdys.

5.3.3 Grafinis grupių palyginimas

Kai turite du skirtingo tipo kintamuosius (vienas – kategorinis, kitas – kiekybinis), dažnai norite palyginti tolydžiojo skirstinio reikšmes kategorinio kintamojo pogrupiuose. Šiuo atveju tarpusavyje palyginkite grupių (centro) padėtį, sklaidą ir imties dydį (tuos pačius dalykus, kuriuos reikia apsirašyti atliekant aprašomąją statistiką). Taip pat panagrinėkite kiekvienos grupės savybes atskirai. Keletas pavyzdžių pateikta žemiau (pav. 5.15–5.18).

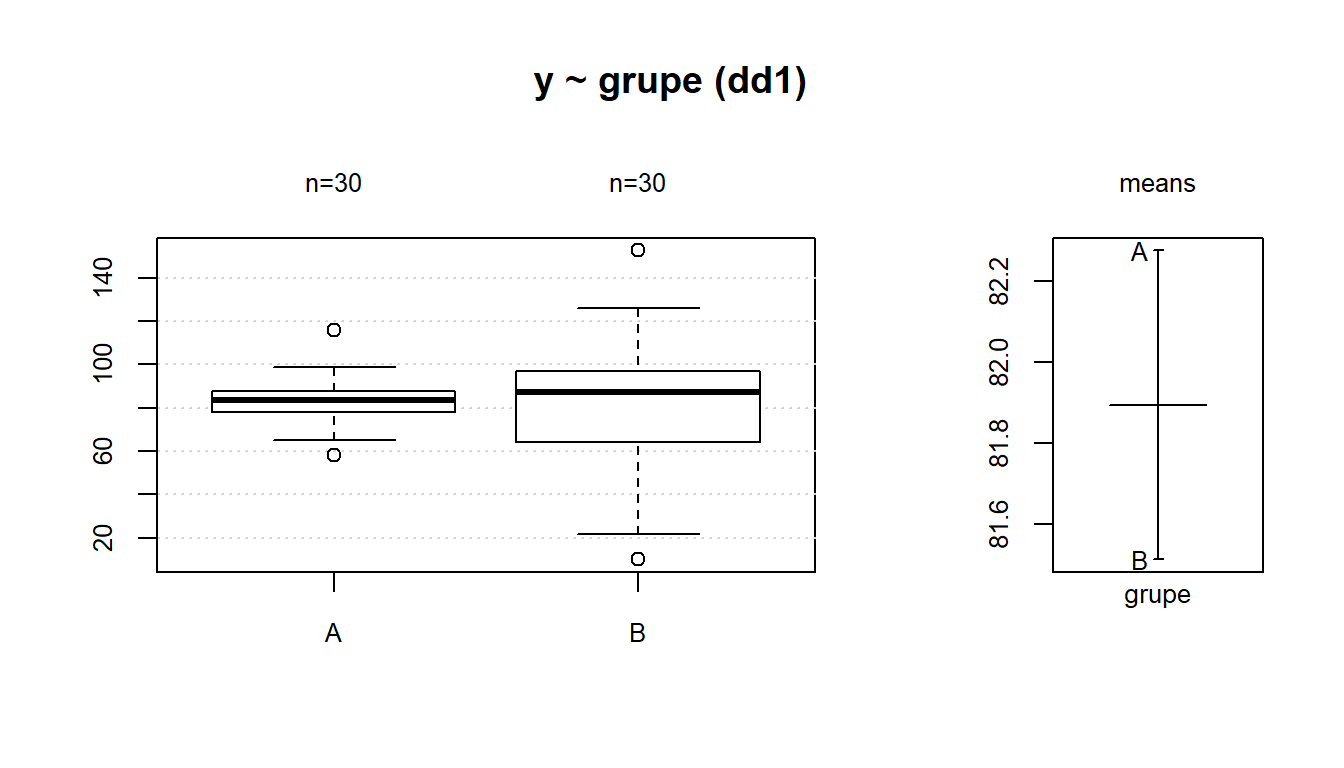
Grupės, kurių sklaida skiriasi, o skirstinio padėtis -- panaši. Grafikas nubraižytas programos „R“ funkcija `DescTools::Desc()`{.r}.

Pav. 5.15: Grupės, kurių sklaida skiriasi, o skirstinio padėtis – panaši. Grafikas nubraižytas programos „R“ funkcija DescTools::Desc().

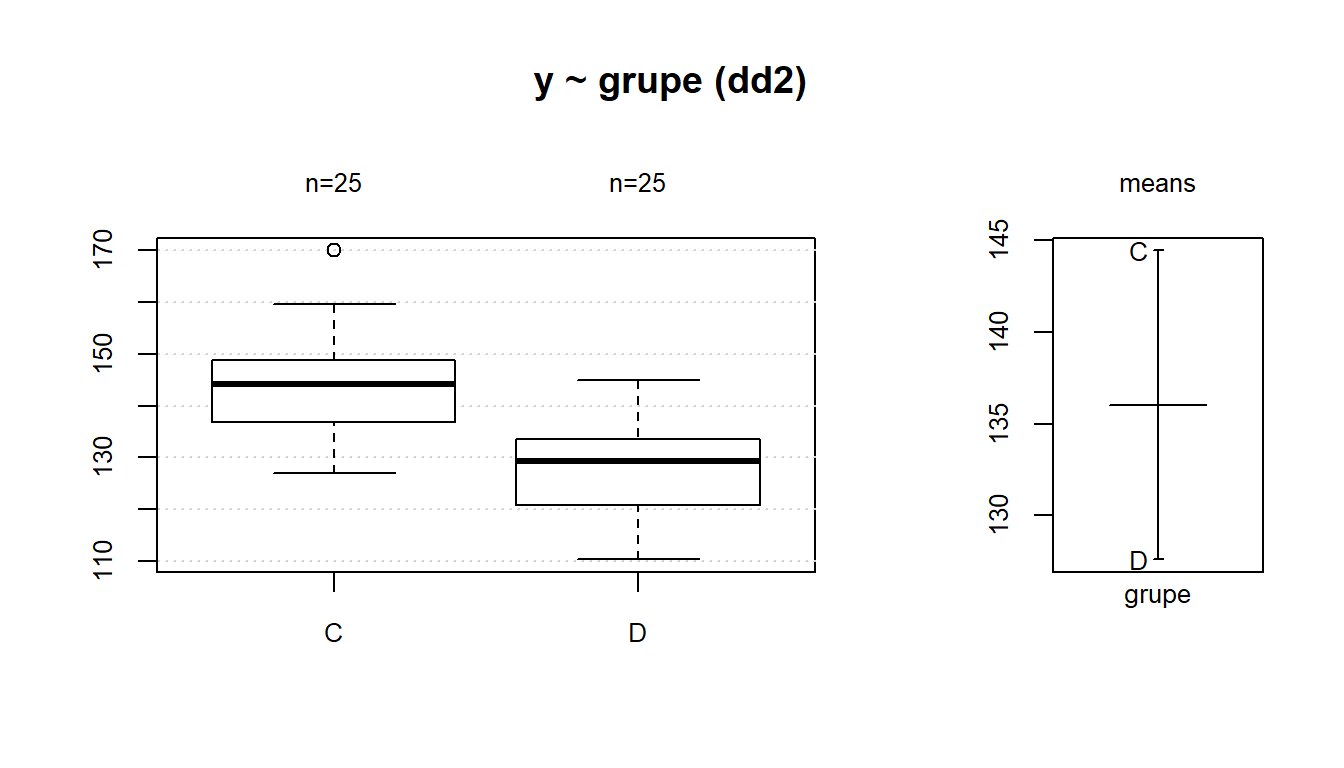
Grupės, kurių sklaida daugmaž vienoda, o skirstinio padėtis -- skirtinga.

Pav. 5.16: Grupės, kurių sklaida daugmaž vienoda, o skirstinio padėtis – skirtinga.

Grupės, kurių ir sklaida, ir skirstinio padėtis skiriasi.

Pav. 5.17: Grupės, kurių ir sklaida, ir skirstinio padėtis skiriasi.

Pagal pradinius kriterijus peržvelgę grafikus, toliau turime išsamiau paanalizuoti (tam gali prireikti papildomų grafikų ar skaitinių suvestinių, jei nesimato):

  1. centro padėtį:
    • kokie centrai matomi? Vidurkiai, medianos, modos?
    • ar centrai labai nutolę vienas nuo kito?
    • kurios grupės reikšmės vidutiniškai didžiausios, kurios – mažiausios?
  2. viso skirstinio padėtį:
    • ar grupių reikšmės (skirstiniai) smarkiai persidengia?
  3. sklaidą:
    • ar visų grupių sklaida daugmaž vienoda?
  4. imties dydį:
    • ar apskritai duomenų yra pakankamai daug? T.y., ar galiu pasitikėti tuo, ką vaizduoja grafikas?
    • ar visos grupės pakankamo dydžio? (Galbūt tik vienoje grupėje per mažai duomenų?)
    • ar grupių dydžiai daugmaž vienodi?
  5. skirstinio formą:
    • ar visų grupių forma daugmaž vienoda?
    • ar simetriška?
      • jei ne, kokia asimetrija?
      • ar asimetrija smarki? Gal tik neženkli?
    • viena ar kelios viršūnės?
    • ar yra labai didelių išskirčių, kurios paveiks rezultatus?
    • ar kiekvienos grupės duomenys yra normalieji?
  1. kitus ypatingus ar neįprastus bruožus, jei tokių yra.

Jei reikia, savo pastebėjimus patikslinkite žiūrėdami į aprašomųjų statistikų lentelę, kurioje kiekviena grupė aprašyta atskirai (pvz., lentelė 5.1).

Lentelė 5.1: Grupių aprašomosios statistikos.
GrupėnPraleistaVidurkisSDMedianaMADIQRAsimetrija
A30082.311.083.57.99.60.48
B30081.529.187.321.430.9-0.31
C250144.510.2144.27.611.90.39
D250127.68.8129.47.212.8-0.22
E31096.432.599.824.028.40.52
F31070.28.271.87.09.5-0.26

Visos 6 anksčiau demonstruotos grupės viename grafike (pav. 5.18).

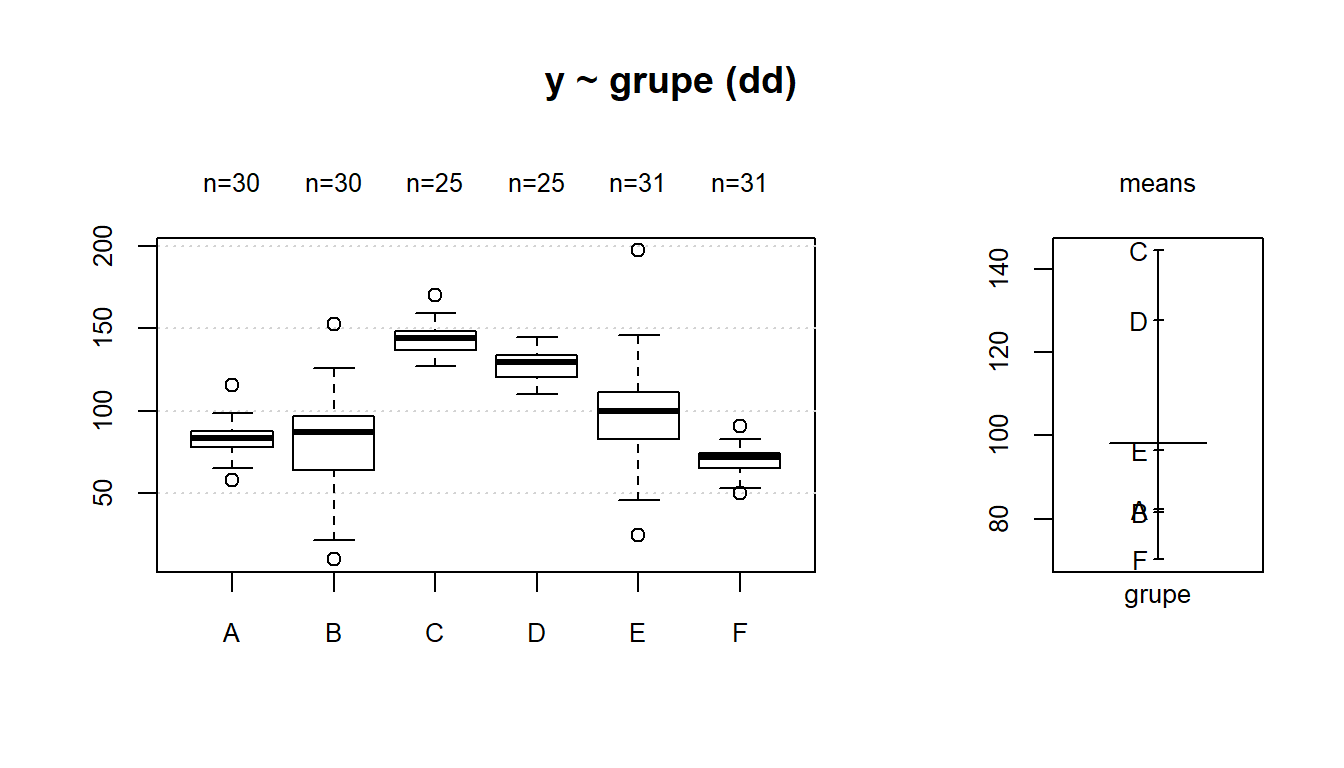
Duomenys (grupės A-F), kurie buvo atvaizduoti aukščiau esančiuose grafikuose.

Pav. 5.18: Duomenys (grupės A-F), kurie buvo atvaizduoti aukščiau esančiuose grafikuose.

5.3.4 Mozaikinė diagrama

Mozaikinė, arba Marimekko, diagrama – tai grafikas dviejų ar daugiau kategorinių kintamųjų reikšmėms atvaizduoti. Šiame skyriuje nagrinėsime atvejį, skirtą lygiai dviems kategoriniams kintamiesiems (pvz., lentelėje 5.2).

Lentelė 5.2: Kategorinių kintamųjų poros pavyzdys. Kelios pirmosios eilutės.
LytisApavas
VyrasBateliai
MoterisBasutės
MoterisBateliai
VyrasŠlepetės
MoterisBasutės
MoterisŠlepetės

Žingsniai, kaip sudaryti mozaikinę diagramą:

  1. Turime 2 kategorinius kintamuosius (sakykime, lytis - vyras ir moteris – ir apavo tipas – bateliai, basutės, šlepetės);
  2. Lape nubrėžiame kvadratą, kurio vienoje ašyje parašome vieno, kitoje ašyje – kito kintamojo pavadinimą (sakykime, x ašyje yra lytis).
  3. Sudarome dažnių lentelę pagal vieną kintamąjį (pasirenkame savo nuožiūra). Pvz., suskaičiuojame, kiek procentų vyrų ir moterų yra imtyje;
  4. Pagal gautą santykį, proporcingai padaliname x ašies ilgį į stačiakampius: kiekvienos grupės dažnis proporcingas kategoriją atitinkančio stačiakampio ilgiui.
  5. Kiekviename pirmo kintamojo pogrupyje suskaičiuojame antrojo kintamojo dažnį:
    • Vyrams: kiek su bateliais, basutėmis bei šlepetėmis;
    • Moterims: kiek su bateliais, basutėmis bei šlepetėmis;
  6. Pagal gautas proporcijas y ašies kryptimi sudaliname kiekvieną prieš tai nubraižytą (t.y., vyrų ir moterų) stačiakampį: pogrupio dažnis proporcingas stačiakampio aukščiui. Atkreipkite dėmesį į tai, kad gavome atskiras proporcijas vyrams, atskiras – moterims.
  7. Susidariusių stačiakampių skaičius lygus pirmo ir antro kintamojo galimų reikšmių sandaugai. Šiuo atveju \(2 \times 3 = 6\). Stačiakampio plotas proporcingas pogrupio dydžiui.

Turbūt akivaizdu, kad iš tų pačių duomenų galime gauti dvi skirtingas mozaikines diagramas (todėl toliau bus vaizduojamos dvi diagramos), priklausomai nuo to, kurį kintamąjį pasirinkome dalinti pirmiausia.

Kaip pagal mozaikinę diagramą įvertinti sąsajos tarp kintamųjų stiprumą? Jei pirmo kintamojo pogrupiuose proporcijos yra vienodos – kintamieji yra nepriklausomi. Jei skirtingos – tada priklausomi. Kuo skirtumas tarp proporcijų didesnis, tuo ryšys yra stipresnis.

Mozaikinės diagramos trūkumas – nesimato imties dydžio, tik santykinis pasiskirstymas.

Paveikslai 5.19–5.27 vaizduoja įvairius mozaikinėmis diagramomis pateiktus simuliuotų ir tikrų duomenų atvejus. Išnagrinėkite juos.

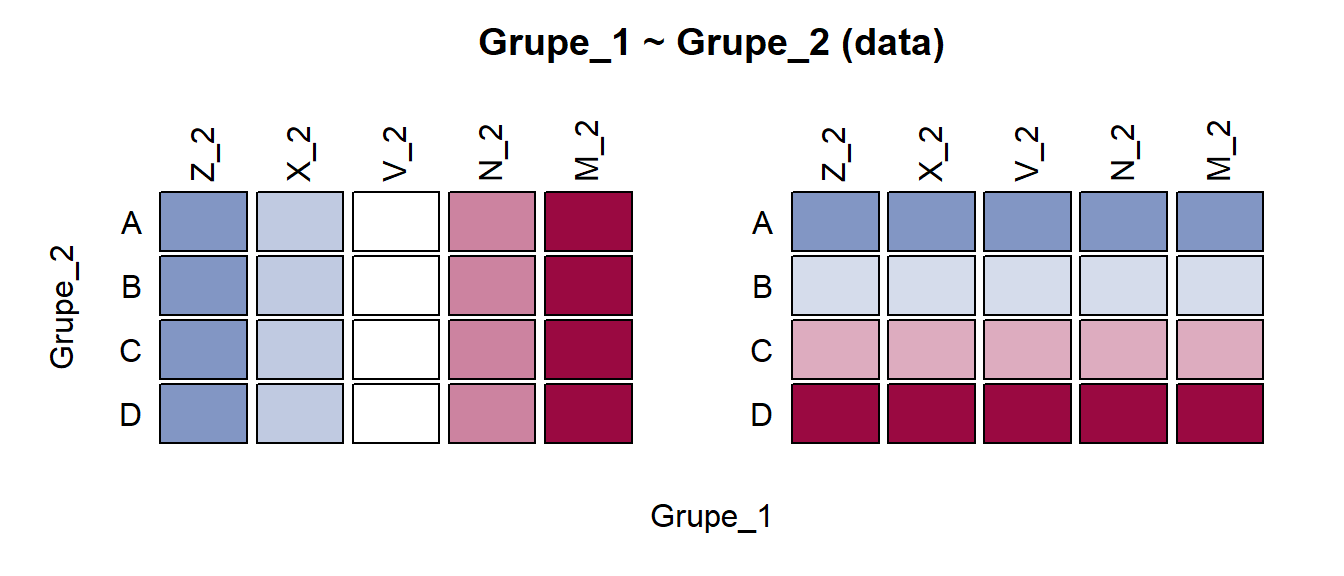
Mozaikinė diagrama: visiškai nepriklausomi kintamieji, vienodi pogrupių dydžiai. Kramerio V = 0.

Pav. 5.19: Mozaikinė diagrama: visiškai nepriklausomi kintamieji, vienodi pogrupių dydžiai. Kramerio V = 0.

Mozaikinė diagrama: visiškai nepriklausomi kintamieji, skirtingi pogrupių dydžiai. Kramerio V = 0.

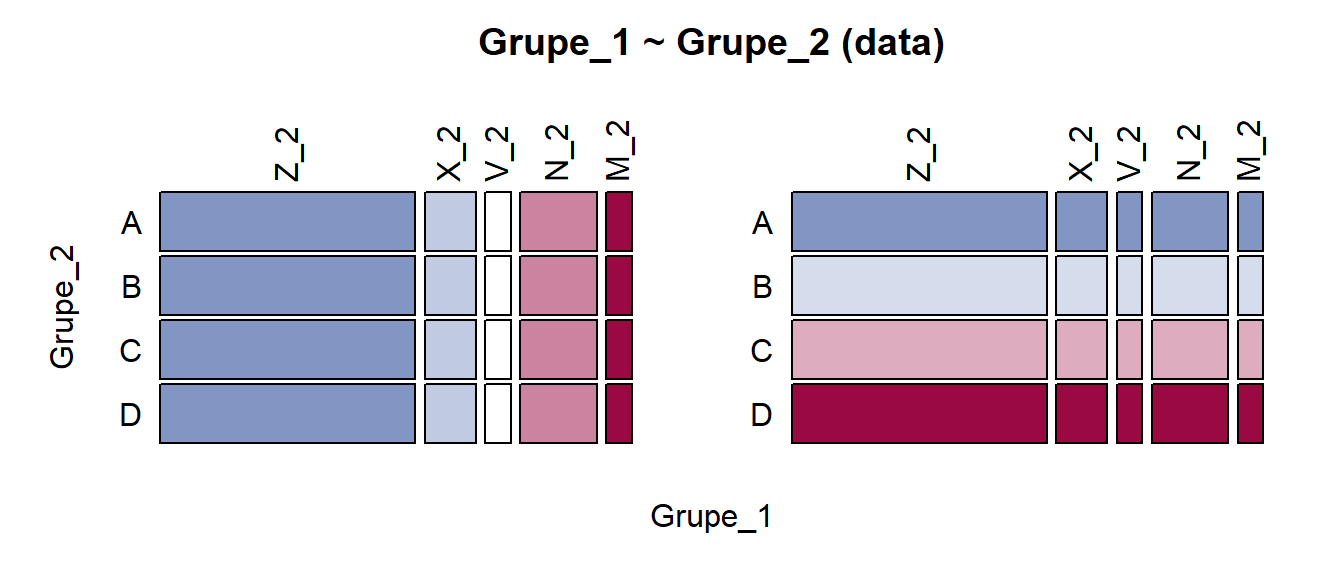
Pav. 5.20: Mozaikinė diagrama: visiškai nepriklausomi kintamieji, skirtingi pogrupių dydžiai. Kramerio V = 0.

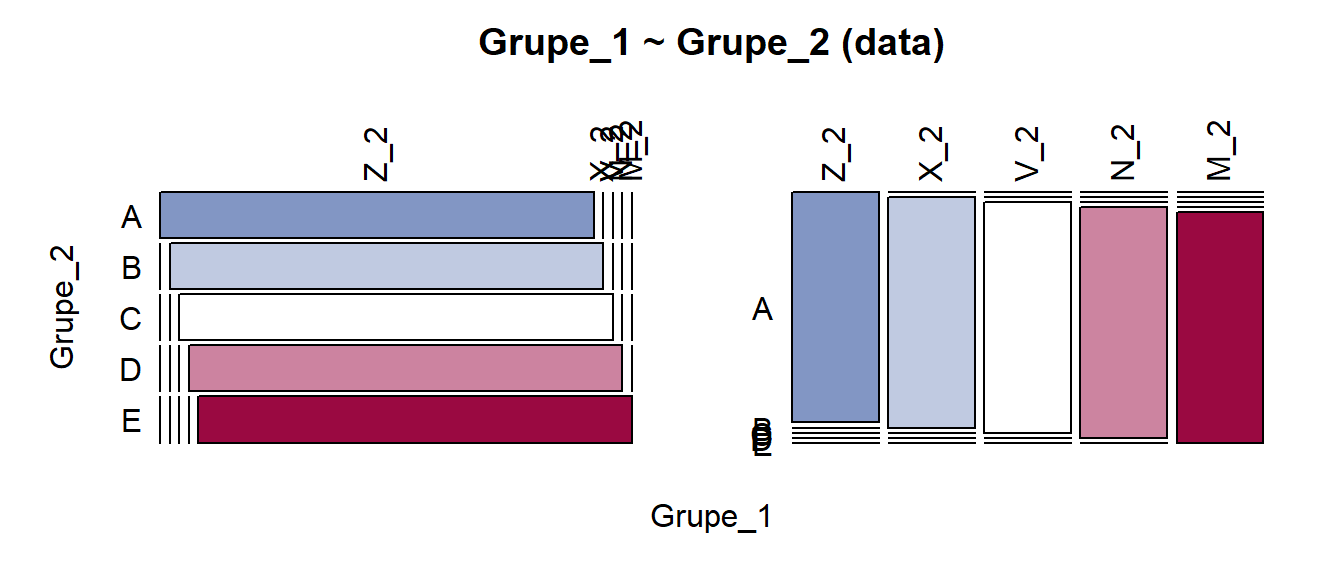
Mozaikinė diagrama: visiškai priklausomi kintamieji, vienodi pogrupių dydžiai. Brūkšneliai (sakykim, ties Z_2 ir E) rodo, kad tose vietose pogrupio dydis lygus nuliui. Kramerio V = 1.

Pav. 5.21: Mozaikinė diagrama: visiškai priklausomi kintamieji, vienodi pogrupių dydžiai. Brūkšneliai (sakykim, ties Z_2 ir E) rodo, kad tose vietose pogrupio dydis lygus nuliui. Kramerio V = 1.

Mozaikinė diagrama: visiškai priklausomi kintamieji, vienodi pogrupių dydžiai, bet skirtingų kintamųjų reikšmės susijusios kitokia eilės tvarka. Kramerio V = 1.

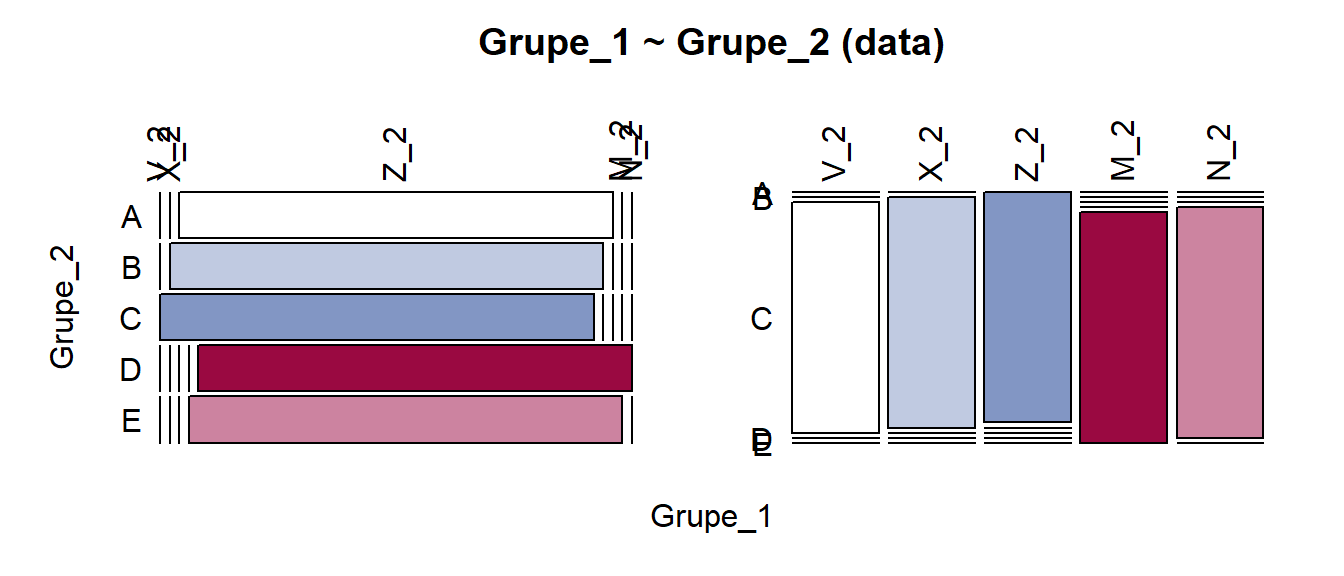
Pav. 5.22: Mozaikinė diagrama: visiškai priklausomi kintamieji, vienodi pogrupių dydžiai, bet skirtingų kintamųjų reikšmės susijusios kitokia eilės tvarka. Kramerio V = 1.

Mozaikinė diagrama: visiškai priklausomi kintamieji, skirtingi pogrupių dydžiai. Kramerio V = 1.

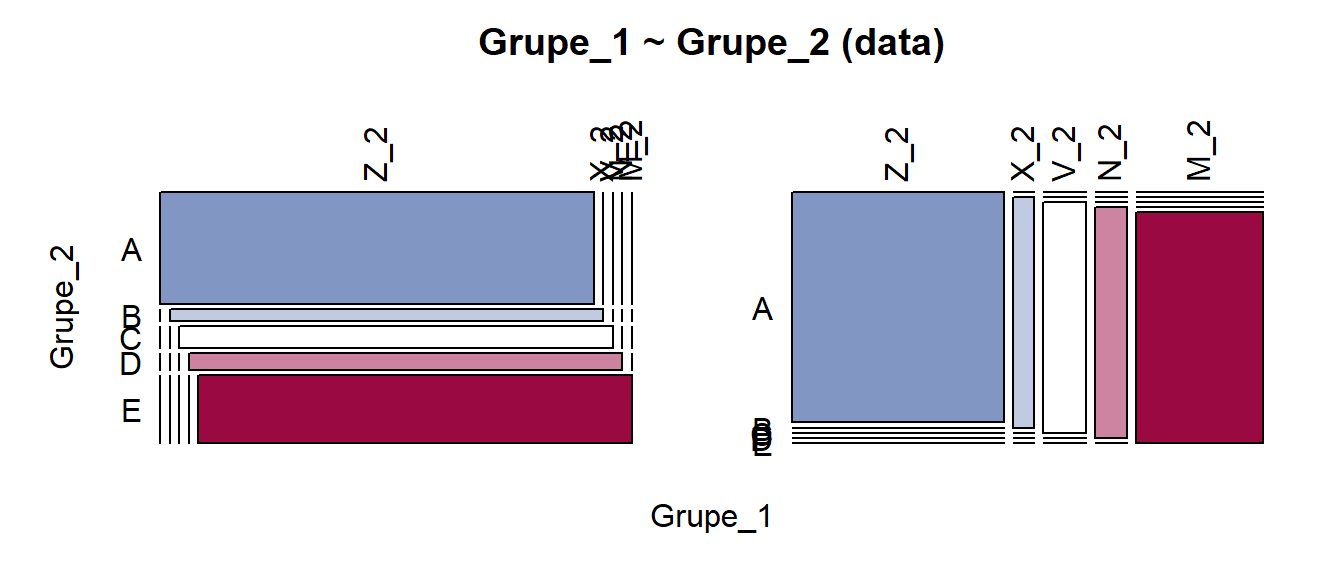
Pav. 5.23: Mozaikinė diagrama: visiškai priklausomi kintamieji, skirtingi pogrupių dydžiai. Kramerio V = 1.

Mozaikinė diagrama: visiškai priklausomi kintamieji, skirtingi pogrupių dydžiai, o skirtingų kintamųjų reikšmės susijusios kitokia eilės tvarka. Kramerio V = 1.

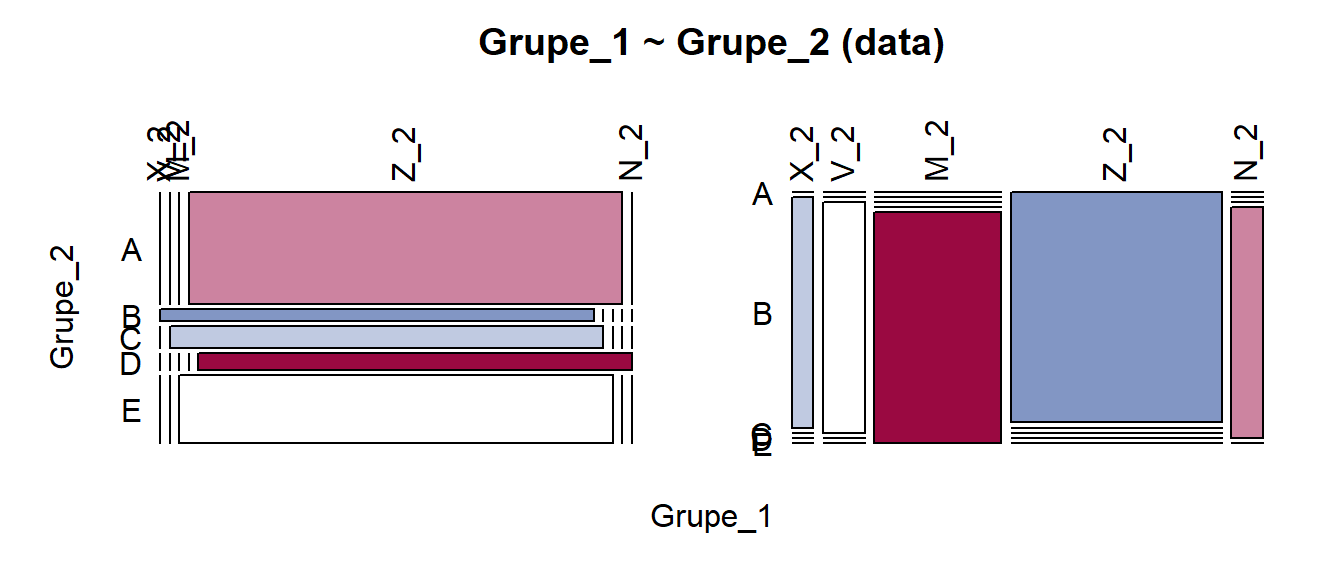
Pav. 5.24: Mozaikinė diagrama: visiškai priklausomi kintamieji, skirtingi pogrupių dydžiai, o skirtingų kintamųjų reikšmės susijusios kitokia eilės tvarka. Kramerio V = 1.

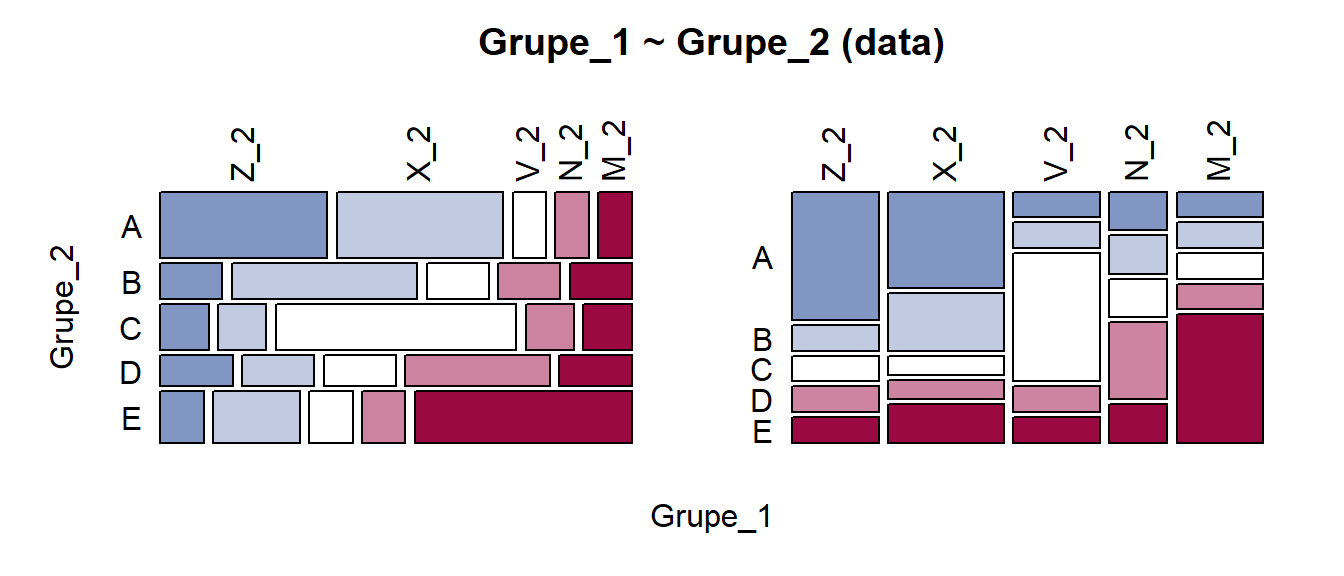
Mozaikinė diagrama: priklausomi kintamieji (1). Kramerio V = 0.34.

Pav. 5.25: Mozaikinė diagrama: priklausomi kintamieji (1). Kramerio V = 0.34.

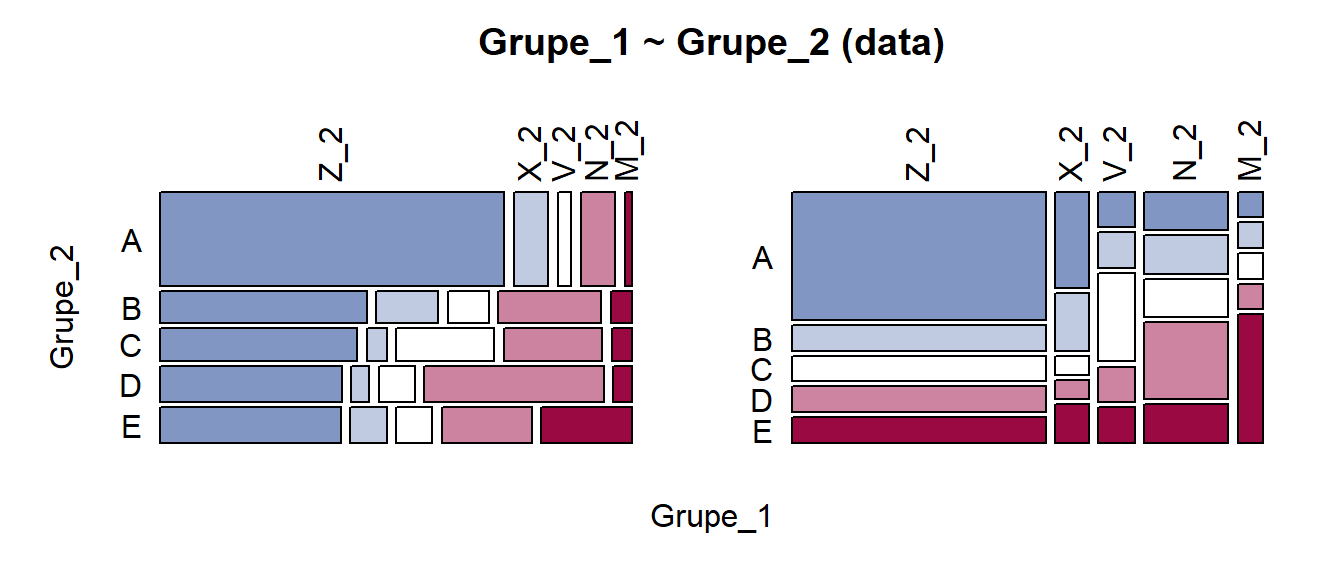
Mozaikinė diagrama: priklausomi kintamieji (2). Kramerio V = 0.25.

Pav. 5.26: Mozaikinė diagrama: priklausomi kintamieji (2). Kramerio V = 0.25.

Mozaikinė diagrama: sąsaja tarp akių ir plaukų spalvos. Tyrimo [@Fisher1940], vykdyto viename iš Škotijos regionų, rezultatai. Kramerio V = 0.28. Pastebėkite, kad lyginant su tamsiaplaukiais, šviesiaplaukiai buvo linkę dažniau turėti šviesias akis.

Pav. 5.27: Mozaikinė diagrama: sąsaja tarp akių ir plaukų spalvos. Tyrimo (Fisher 1940), vykdyto viename iš Škotijos regionų, rezultatai. Kramerio V = 0.28. Pastebėkite, kad lyginant su tamsiaplaukiais, šviesiaplaukiai buvo linkę dažniau turėti šviesias akis.

5.3.5 Stulpelinės diagramos pogrupiams

Kaip alternatyva mozaikinėms gali būti naudojamos stulpelinės diagramos pogrupiais (pav. 5.28).

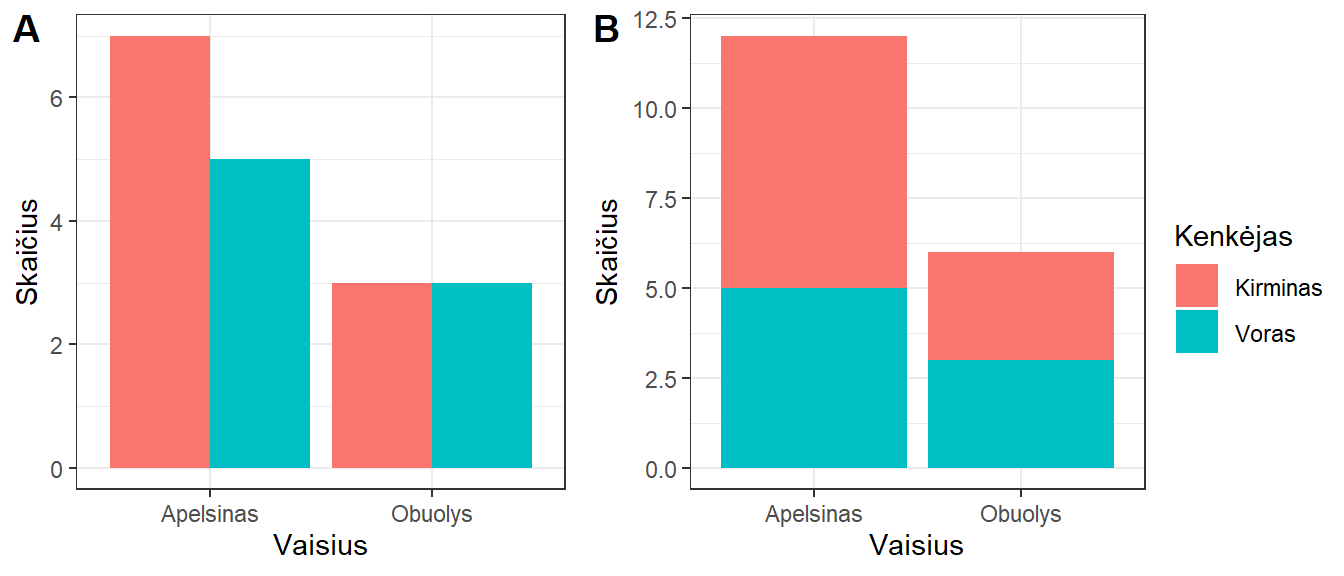
Du stulpelinių diagramų pogrupiais pavyzdžiai: stulpeliai greta bei vienas ant kito.

Pav. 5.28: Du stulpelinių diagramų pogrupiais pavyzdžiai: stulpeliai greta bei vienas ant kito.

Informacijos šaltiniai

Čekanavičius V., Murauskas G. Statistika ir jos taikymai I. Vilnius: TEV (2006).
Field A., Miles J., Field Z. Discovering Statistics Using R. London: Sage (2012). Prieiga per internetą: https://us.sagepub.com/en-us/nam/discovering-statistics-using-r/book236067.
Fisher R.A. Steps of the Scientific Method, 10 (1940). DOI: 10.1111/j.1469-1809.1940.tb02264.x.
Fisher R.A. The Analysis of Covariance Method for the Relation between a Part and the Whole, Biometrics 3(2): 65 (1947). DOI: 10.2307/3001641.
Venclovienė J. Statistiniai metodai medicinoje. Kaunas: Vytauto didžiojo universitetas (2010). Prieiga per internetą: https://www.vdu.lt/cris/bitstream/20.500.12259/271/1/ISBN9789955125587.pdf.