18. Padėties lyginimas (1-2 imtims)

Tikslas – susipažinti su statistinių hipotezių apie skirstinių arba jų parametrų (pvz., vidurkių) padėtį tikrinimo būdais vienai bei dviems imtims.

Sakykime, turime kurią nors iš šių situacijų:

sporto klube mums siūlo treniruočių programą, kuri, kaip teigia treneriai, per pirmąjį mėnesį padeda sulieknėti vidutiniškai bent 5 kilogramais;
farmacininkai teigia sukūrę naują vaistą, kuris pailgina miego trukmę;
norime sužinoti, kas greičiau įsimena informaciją – vyrai ar moterys;
norime patikrinti, kuris standartinės terpės priedas – gliukozė ar fruktozė – leidžia užauginti daugiau ląstelių;
fermeris nori ištirti, kuriuo iš 6 pašarų geriausia šerti viščiukus, kad jie per 6 savaites užaugtų didžiausi.

Visoms šioms situacijoms bendra tai, kad atlikdami tyrimą surinktume vieną ar kelias kiekybinių duomenų grupes ir lygindami grupes tirtume (žiūrint matematiškai), ar kažkurios grupės reikšmės yra linkusios būti didesnės ar mažesnės, ar jos daugmaž vienodos:

ar tikrai vidutiniškai numetama daugiau nei 5 kg svorio?
ar tikrai vartojant vaisto miegama ilgiau nei nevartojant?
ar tikrai skiriasi vyrų ir moterų per 1 minutę įsimintų žodžių skaičius?
ar tikrai terpėje su gliukoze ir fruktoze užauga skirtingas ląstelių skaičius?
ar tikrai viščiukų svoris skiriasi, jei juos šeriame skirtingais pašarais?

Turime kelias kiekybinių duomenų grupes ir lyginame jų skirstinių padėtį.

Tad norint atsakyti į išsikeltus klausimus, mums reikia taikyti statistinius skirstinių padėties lyginimo kriterijus. Jie padeda įvertinti, ar tikėtina, kad tyrimo metu gauti būtent tokie rezultatai dėl to, kad, pvz., buvo lankytos būtent šios sporto klubo treniruotės, ar, visgi, juos galima paaiškinti vien tik atsitiktinumu (ar su treniruotėmis nesusijusiais veiksniais). Tai vieni dažniausiai naudojamų statistinių kriterijų, tad apie jų taikymą, kai turime 1 ar lygiai 2 duomenų grupes, bus kalbama šiame, o kai turime kelias (2 ar daugiau) grupes – kitame („19 ANOVA ir jos analogai“) skyriuje.

Tiriame, ar skirtumai tarp grupių padėties yra statistiškai reikšmingi.

Tai vienas iš dažniausiai naudojamų analizės tipų.

18.1 Pasirinkimų schema

Renkantis analizės metodą reikia atsižvelgti į iškeltą klausimą ir duomenų savybes: lyginamų grupių skaičių ir ar tos grupės nepriklausomos, ar priklausomos (porinės, kartotinės). Svarbu patikrinti, ar tenkinama normalumo prielaida (ar kiekviena grupė skirstosi daugmaž pagal normalųjį skirstinį; plačiau skaitykite skyriuje „16 Normalumo tikrinimas“). Jei grupės pakankamo dydžio ir skirstosi normaliai, tada naudosime parametrinius metodus (jiems reiktų teikti pirmenybę, nes jų kriterijaus galia didesnė ir įprastai rezultatus lengviau interpretuoti), kitu atveju – neparametrinius. Taip pat jei turime kelias grupes, reikia patikrinti, ar tenkinama lygių dispersijų prielaida (žr. skyriuje „17 Sklaidos lyginimas“).

Siekiant susisteminti, kaip pasirinkti vieną iš kelių dažniausiai naudojamų metodų, šiame skyriuje pateikiamos schemos. Pav. 18.1 pateikti pirmieji kriterijaus pasirinkimo žingsniai (tad prieš analizuodami kitas schemas, šią turite suprasti labai gerai). Pav. 18.2 pateikta detalesnė pasirinkimo schema, kai turime 1 arba 2 grupes. Atkreipkite dėmesį, kad:

Matematiškai žiūrint, priklausomų (porinių, kartotinių) imčių ir atitinkami vienos imties ($t$ ir $t$, Wilcoxon ir Wilcoxon) kriterijai – tai tas pats modelis, tik porinių imčių atveju pirmiausia apskaičiuojamas skirtumas ir taip gaunama viena duomenų imtis. Tada ji analizuojama. Dėl to kai kurios vienos imties ir porinių imčių analizės sutampa. Tarkime, porinių imčių analizės prielaidas tikriname naudodami ne pačių imčių duomenis, o skirtumus tarp jų. Taip paprasčiau ir patikimiau. Taip pat punktyrais pažymėta, kad apskaičiavus skirtumus tarp porinių imčių, toliau analizę galima tęsti, tarsi tai būtų vienos imties tyrimas.
Pasak Zimmerman (2004), Velčo (Welch) $t$ kriterijus (skirtas nepriklausomoms imtims) yra pakankamai tikslus ir toms situacijoms, kai gali būti taikomas Stjudento $t$ kriterijus. Tad kai kurios vietos schemos 18.2 vienos yra pažymėtos punktyrais kaip alternatyvi tyrimo eiga.
Iš tiesų yra daugiau galimų metodų, kurie tam tikroms situacijoms galimai tiktų labiau. Tačiau schemoje apsiribota tik dažniausiai naudojamais.

Schemos yra supaprastintos ir tik rekomendacinio pobūdžio. Jų tikslas – būti „atspirties tašku“ renkantis analizės metodą. Konkrečiu atveju gali būti išlygų, papildomų sąlygų arba kitų pasirinkimo variantų, kurie schemoje nepažymėti.

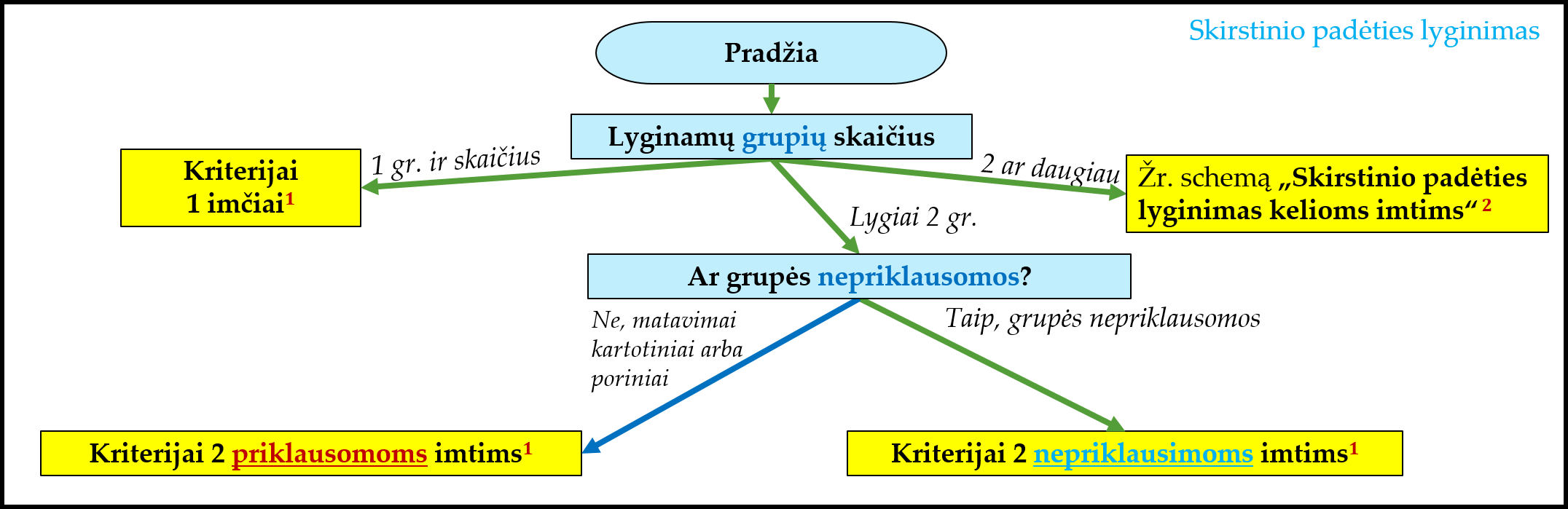
Pav. 18.1: Bendroji schema, rekomenduojanti, kurį skirstinių padėties lyginimo metodą pasirinkti. Paaiškinimai pateikti žemiau.

Schemoje 18.1 skaičiais pažymėtų punktų paaiškinimai:
¹ toliau žiūrėti schemą 18.2;
² toliau žiūrėti schemą 19.1 (kitame skyriuje).

$Schema, rekomenduojanti, kurį skirstinio **padėties** lyginimo metodą pasirinkti, kai lyginamos 1-2 imtys (grupės). Spalvinio žymėjimo reikšmės pateiktos skyriuje „\@ref(ht-schemos) [Schemos metodams pasirinkti](#ht-schemos)“.$

Pav. 18.2: Schema, rekomenduojanti, kurį skirstinio padėties lyginimo metodą pasirinkti, kai lyginamos 1-2 imtys (grupės). Spalvinio žymėjimo reikšmės pateiktos skyriuje „12.4 Schemos metodams pasirinkti“.

Reikia pasirinkti ir taikyti tik vieną jūsų situacijai labiausiai tinkantį padėties lyginimo kriterijų.

Schemoje 18.2 skaičiais pažymėtų punktų paaiškinimai:
¹ Jei norima išvadas daryti apie medianą, vienos imties ar dviejų imčių porų skirtumo skirstinys turi būti simetriškas vidurkio (medianos) atžvilgiu. Kitu atveju išvados bus bendresnės: tik apie grupės reikšmių „polinkį“ būti didesnėms ar mažesnėms. Kaip alternatyva šiam Vilkoksono kriterijui (angl. Wilcoxon Signed Rank test) tam tikrais atvejais gali būti naudojamas ženklų kriterijus (angl. Sign test).
² Prielaidos turėtų būti tikrinamos porų ar pakartojimų skirtumų skirstiniui.
³ Pasiskirstymo normalumas tikrinamas kiekvienai grupei atskirai. Pvz., nusibraižant normaliąją QQ diagramą ir taikant normalumo (pvz., Shapiro-Wilk) kriterijų. Apie normalumo tikrinimą rašoma 16 skyriuje. Jei kiekviena analizuojama imtis yra pakankamai didelė, schemoje nurodyti parametriniai metodai nėra labai jautrūs mažam ar vidutinio dydžio nuokrypiui nuo normalumo.
⁴ Sprendžiant „iš akies“, skirtumas tarp didžiausios ir mažiausios dispersijos neturėtų būti didesnis kaip 3 kartus. Lygių dispersijų prielaidai tikrinti įprastai naudojamas Levene‘o kriterijus su Brown-Forsythe pataisa (centras – mediana). Apie tai plačiau rašoma skyriuje 17.
⁵ Nereikalaujama, kad dispersijos būtų lygios.
⁶ Šiuo atveju skirstinių forma laikoma vienoda (panašia), kai visų grupių asimetrija yra vienos krypties ir panašaus stiprumo, o sklaida – daugmaž vienoda (pav. 18.3). Tokiems atvejams metodas yra tinkamas labiausiai.
⁷ Jei grupių skirstinių forma panaši ir skiriasi tik poslinkio parametru, t.y., skiriasi skirstinio padėtis (tokiems duomenims ir rekomenduojamas Mann-Whitney-Wilcoxon kriterijus), tada galime daryti išvadas apie grupių medianas: tokiu atveju rezultatai informatyvesni nei 8 punkto atveju;
⁸ Jei lyginamų grupių skirstinių forma skirtinga (skiriasi dispersijos, būdinga skirtingos krypties asimetrija), išvadas darome tik apie tai, ar kažkurios grupės reikšmės linkusios būti statistiškai didesnės/mažesnės/kitokios, bet ne apie medianas: šiuo atveju rezultatai mažiau informatyvūs nei 7 punkto atveju. Kriterijaus galia taip pat mažesnė. Tokiais atvejais (Čekanavičius ir Murauskas 2004, p.25–28) rekomenduoja Voldo-Volfovitso (Wald-Wolfowitz) kriterijų dviems imtims.
⁹ Žiūrėti schemą 19.1 (kitame skyriuje).

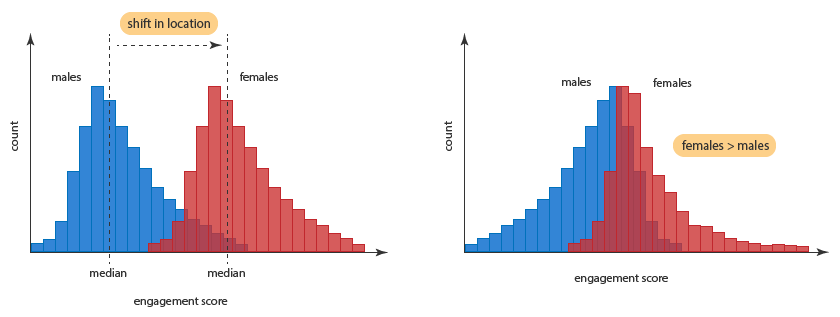
Pavyzdys, kaip atrodo panašios formos skirstiniai, besiskiriantys tik padėtimi, (kairėje) ir skirtingų formų skirstiniai (dešinėje).
Skirstinio forma lemia, kokio tipo išvadas galime daryti: apie medianas ar apie padėtį bendrai. (Copyright 2014. Laerd Statistics).

Pav. 18.3: Pavyzdys, kaip atrodo panašios formos skirstiniai, besiskiriantys tik padėtimi, (kairėje) ir skirtingų formų skirstiniai (dešinėje). Skirstinio forma lemia, kokio tipo išvadas galime daryti: apie medianas ar apie padėtį bendrai. (Copyright 2014. Laerd Statistics).

18.2 Statistinės hipotezės lyginant padėtį

Toliau aptarsime, kaip formuluojamos statistinės hipotezės parametrinių ir neparametrinių kriterijų taikymo atveju.

18.2.1 Parametriniai kriterijai

Jei taikome parametrinius kriterijus, tada situacija labai paprasta: tikriname, ar skirtumai tarp vidurkių (arba vidurkio ir skaičiaus) yra reikšmingi. Vidurkiai ir yra tas skirstinio parametras, kurį lyginame. Tad dviejų grupių atveju statistinės hipotezės formuluojamos taip:

$H_0$: vidurkiai yra lygūs, $\mu_1=\mu_2$ (skirtumo nėra);
$H_1$:
- arba vidurkiai skiriasi $\mu_1 \ne \mu_2$ (dvipusė alternatyva),
- arba $\mu_1>\mu_2$ (vienpusė alternatyva),
- arba $\mu_1<\mu_2$ (vienpusė alternatyva).

Tad pasirenkame vieną iš 3 galimų hipotezių porų. (Apie tai nusprendžiame tyrimo planavimo etape.)

Jei reikšmingumo lygmuo $\alpha = 0{,}05$, tai, kai:

$p\ge0{,}05$, teigiame, kad skirtumas tarp vidurkių yra statistiškai nereikšmingas ir nulinės hipotezės $H_0$ atmesti nėra pagrindo, užregistruotą skirtumą galime paaiškinti vien tik atsitiktinumu.
$p<0{,}05$, atmetame $H_0$ ir priimame $H_1$. T.y., teigiame:
- arba kad skirtumas tarp vidurkių yra statistiškai reikšmingas (jei dvipusė alternatyva),
- arba kad pirmos grupės vidurkis yra statistiškai reikšmingai didesnis nei antros (jei vienpusė alternatyva),
- arba kad pirmos grupės vidurkis yra statistiškai reikšmingai mažesnis nei antros (jei vienpusė alternatyva).

Jei turime tik vieną grupę ir skaičių, tai hipotezėse vietoje antrosios grupės vidurkio įrašome tą skaičių. Aprašant rezultatus turi būti pateikti vidurkiai ir kitos su jais suderintos statistikos.

18.2.2 Neparametriniai kriterijai

Jei situacijai tinka neparametriniai kriterijai, tada formuluojamos bendresnės hipotezės: ne apie konkretų parametrą, bet apskritai apie bendrą skirtumą tarp skirstinių padėties. Tarkime, lyginamos dvi duomenų grupės $Y_1$ ir $Y_2$ (tegu $b$ – bet koks skaičius). Tada:

$H_0$: poslinkis tarp skirstinių padėties yra lygus nuliui (skirtumo nėra). Arba matematiškai: $P(Y_1>b) = P(Y_2>b)$ kiekvienam $b$;
$H_1$:
- arba poslinkis tarp skirstinių padėties nelygus nuliui (kažkurios iš grupių reikšmės yra linkusios būti didesnės), skirstinių padėtis skiriasi, t.y., $P(Y_1>b) \ne P(Y_2>b)$ kiekvienam $b$ (jei dvipusė alternatyva),
- arba pirmos grupės reikšmės yra linkusios būti didesnės nei antrosios, t.y., $P(Y_1>b) > P(Y_2>b)$ kiekvienam $b$ (jei vienpusė alternatyva),
- arba pirmos grupės reikšmės yra linkusios būti mažesnės nei antrosios, t.y., $P(Y_1>b) < P(Y_2>b)$ kiekvienam $b$ (jei vienpusė alternatyva).

Tad pasirenkame vieną iš 3 galimų hipotezių porų. Apie tai nusprendžiame tyrimo planavimo etape. Pavyzdys, kaip skirstiniai gali atrodyti $H_0$ ir $H_1$ atveju pavaizduotas pav. 18.4.

Pavyzdys: nulinės (kairėje) ir alternatyviosios hipotezės (dešinėje) vizualizacija taikant neparametrinius kriterijus.
(Copyright 2014. Laerd Statistics).

Jei reikšmingumo lygmuo $\alpha = 0{,}05$, tai, kai:

$p\ge0{,}05$, teigiame, kad poslinkis (skirtumas) tarp skirstinių yra statistiškai nereikšmingas, nėra pagrindo atmesti $H_0$, skirtumus galime paaiškinti vien tik atsitiktinumu.
$p<0{,}05$, atmetame $H_0$ ir priimame $H_1$. T.y., teigiame:
- arba kad poslinkis (skirtumas) tarp skirstinių yra statistiškai reikšmingas ir kažkurios grupės reikšmės yra linkusios būti didesnės (jei dvipusė alternatyva);
- arba kad pirmos grupės reikšmės yra linkusios būti didesnės nei antrosios (jei vienpusė alternatyva),
- arba kad pirmos grupės reikšmės yra linkusios būti mažesnės nei antrosios (jei vienpusė alternatyva).

Jei turime tik vieną grupę ir skaičių, tai hipotezes formuluojame taip, kad būtų tikrinama, ar grupės reikšmės yra linkusios būti mažesnės/didesnės nei pateiktoji reikšmė.

Jei visų grupių skirstinių formos yra vienodos (vienoda asimetrijos kryptis, daugmaž vienodas asimetrijos stiprumas bei sklaida) ir skirstiniai skiriasi tik poslinkio parametru (tokiems duomenims šie neparametriniai kriterijai yra galingiausi), tada hipotezes galime formuluoti apie medianų skirtumus (pvz., $H_0$ – medianos vienodos, $H_1$ – medianos skiriasi).

Aprašant rezultatus turi būti pateiktos medianos ir kitos su jomis derančios statistikos.

18.3 Efekto dydis

Rezultatai gali tapti statistiškai reikšmingi vien tik dėl to, kad imties dydis labai didelis. Dėl to be statistinio reikšmingumo reiktų nurodyti ir efekto dydį. Efekto dydis būna paprastasis (nestandartizuotas) arba standartizuotasis. Standartizuotieji efekto dydžiai būna r, r² ir d tipų. Jei tinka, pravartu nurodyti keliomis formomis, nes, priklausomai nuo situacijos, kiekviena forma gali turėti savo privalumų. Plačiau šie ir kiti bendrieji principai pristatomi skyriuje „12.2.2 Efekto dydis: skirtumo dydis, paaiškinta kitimo dalis“. Tad jei nesate susipažinę, pirmiausia perskaitykite juos.

Nepaisant to, kokia $p$ reikšmė buvo gauta, tyrėjai privalo tarp rezultatų pateikti ir efekto dydį (Durlak 2009).

18.3.1 Standartizuotieji efekto dydžio matai grupių poroms

Šis skyrius yra skirtas vienos ir dviejų imčių (grupių) padėties lyginimo standartizuotiesiems efekto dydžiams aptarti. Skaičiuojant standartizuotuosius efekto dydžio matus panaikinami matavimo vienetai, dydžiai tampa bedimensiai (standartizuoti). Tai leidžia palyginti skirtingus kintamuosius ar skirtingais matavimo vienetais matuojamus dydžius skirtingų tyrimų metu. Vienos arba dviejų imčių atvejais galima taikyti tiek d, tiek r (bei r²) tipo efekto dydžius.

Lygtys (18.1) ir (18.2) vaizduoja principą, kaip skaičiuojamos $t$ ir $d$ statistikos, tad jų dydis turėtų skirtis maždaug $\sqrt{n}$ kartų. Vienos imties $t$ kriterijaus statistikos skaičiavimo pavyzdys pateiktas (11.1) lygtyje (skyrius „11.5.1 Apie t kriterijaus taikymą ir p reikšmių skaičiavimą“).

\[\begin{equation} t = \frac{\overline{x}_1 - \overline{x}_2}{SE} \tag{18.1} \end{equation}\]

\[\begin{equation} d = \frac{\overline{x}_1 - \overline{x}_2}{SD} \tag{18.2} \end{equation}\]Čia SD – jungtinis standartinis nuokrypis, SE – jungtinė standartinė paklaida, $\overline{x}_1$, $\overline{x}_2$ – grupių vidurkiai. „Jungtinis“ (angl. pooled) reiškia, kad skaičiuojamas atsižvelgiant į grupes. Į matematines detales neisime, bet vienas iš galimų „sujungimo“ būdu – tiesiog paimti kiekvienos grupės SD vidurkį.

Taikant parametrinius kriterijus gali būti skaičiuojamos d tipo statistikos, kurios rodo skirtumą, išreikštą standartiniais nuokrypiais: Koheno $d$ (Cohen’s $d$; SD² – jungtinė grupių dispersija), Hedžo $g$ (Hegde’s $g$; SD² – jungtinė svertinė grupių dispersija), Glaso delta (Glass $\Delta$; SD² – kontrolinės grupės dispersija). Kaip matote, kiekvienu atveju standartiniai nuokrypiai (ar dispersijos) skaičiuojami kitaip. Mažoms imtims (tarkime, n < 50) turėtų būti skaičiuojami koreguotieji (nepaslinktieji) koeficientų variantai (pvz., Koheno $d^*$ su Hedžo pataisa). Matematines detales galite rasti straipsniuose (Tomczak ir Tomczak 2014; Ialongo 2016; Durlak 2009).

Parametriniams kriterijams r ir r² tipo efekto dydis gali būti skaičiuojamas pagal (18.3) [šaltinis nenurodytas] ir (18.4) (Tomczak ir Tomczak 2014; Mordkoff 2019) lygtis. O galimi koeficiento žymėjimai yra $r^2$ ar $\eta^2$ (Tomczak ir Tomczak 2014).

\[\begin{equation} \eta = \frac{t}{\sqrt{t^2+\nu}} \tag{18.3} \end{equation}\]

\[\begin{equation} \eta^2 = \frac{t^2}{t^2+\nu} \tag{18.4} \end{equation}\]

Koeficientas $\eta^2$ (eta kvadratu) laikomas teigiamai paslinktuoju. Nepaslinktasis/Mažiau paslinktasis jo analogas $\omega^2$ (omega kvadratu) gali būti skaičiuojamas pagal (18.5) lygtį (Albers ir Lakens 2018, priedas A). (Pastaba: lygtis buvo išvesta dispersinei analizei, tačiau taikant $t$ kriterijų laikoma, kad $F = t^2$. Visgi, kai $|t| \leq 1$, rezultatai atrodo nekorektiški, nes gaunamas neigiamas $\omega^2$. Tad, matyt, formulę reiktų taikyti tik tada, kai absoliučioji $t$ reikšmė yra pakankamai didelė arba laikyti, kad efekto dydis artimas nuliui.) \[\begin{equation} \omega^2 = \frac{t^2-1}{t^2+\nu+1} \tag{18.5} \end{equation}\]

Čia $\nu$ – laisvės laipsniai, $t$ – kriterijaus statistika.

Koeficientai $\omega^2$ ir $\eta^2$ yra skirtingai skaičiuojami to paties dydžio įverčiai.

Apie tai, kaip vienus efekto dydžio koeficientus perskaičiuoti į kitus, savo straipsnio pabaigoje rašo Durlak (2009) bei ši svetainė .

Neparametriniams kriterijams taip pat galima skaičiuoti r tipo standartizuotuosius efekto dydžius (formulės pateiktos straipsnyje (Tomczak ir Tomczak 2014)).

Vienas iš siūlymų, kaip galima interpretuoti skaitines efekto dydžio reikšmes, pateiktas skyriuje „Standartizuotųjų efekto dydžių interpretacija“. Skirtingų autorių siūlymus, kaip interpretuoti įvairius efekto dydžius, galite rasti čia . Tačiau tai labai subjektyvūs vertinimai: kas vienoje mokslo srityje ar vieno tyrimo metu yra „didelis“ efekto dydis, kitoje situacijoje gali būti „mažas“. Tad geriau savo darbe gautus dydžius vertinti lyginant su kitų jūsų srities tyrėjų darbais.

Efekto dydį kaip „mažą“ ar „didelį“ interpretuokite atsargiai. Visada nurodykite skaitinę išraišką.

Norėdami patyrinėti efekto dydį, matuojamą kaip Koheno $d$, galite pasinaudoti interaktyvia vizualizacija „Interpreting Cohen’s d Effect Size“ . Norėdami pamatyti, kaip nuo koreliacijos koeficiento dydžio priklauso paaiškintos dispersijos dalis, galite naudotis vizualizacija „Interpreting Correlations“ (pastaba: demonstruojamas koreliacijos koeficientas, kai tiriamas ryšys tarp dviejų kiekybinių kintamųjų).

18.4 Rezultatų pateikimas

18.4.1 Rezultatų pavyzdys

Tai – kompiuterine programa gautų rezultatų pavyzdys.

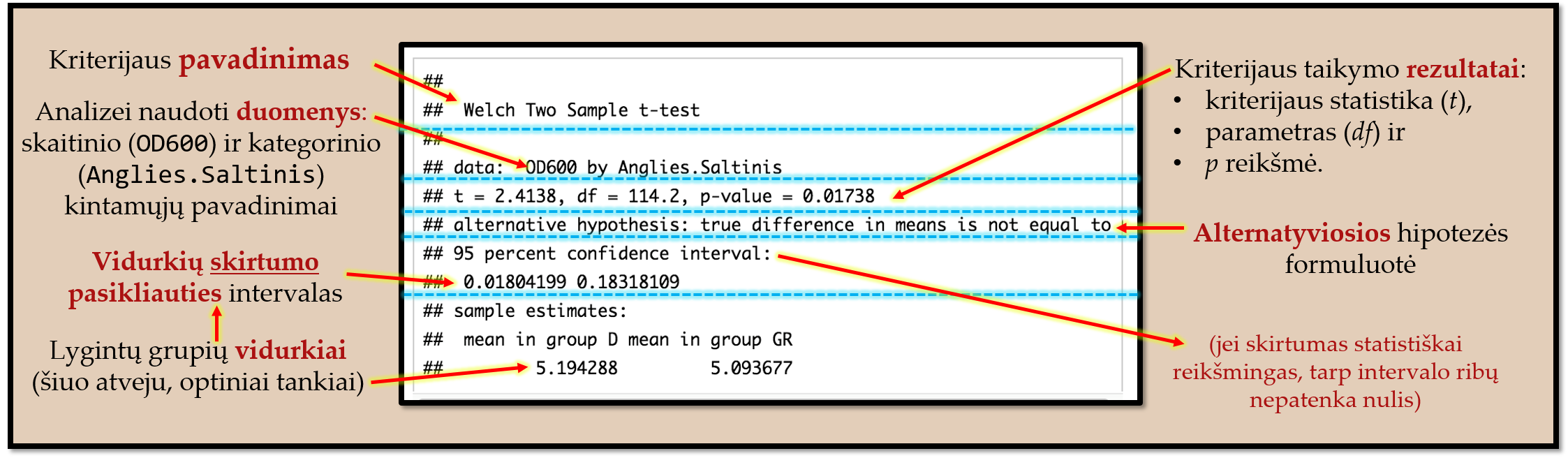
Rezultatų pavyzdys Velčo (Welch) $t$ kriterijų taikant programa „R“ (variantas 1).
Panašios formos rezultatai gaunami taikant ir kitus šiame skyriuje aprašomus kriterijus.
Šiuo konkrečiu atveju lyginamas ląstelių terpių, kuriose yra skirtingas anglies šaltinis, optinis tankis (OD) ties 600 nanometrų.
Laikoma, kad kuo OD didesnis, tuo terpėje daugiau ląstelių.

Pav. 18.5: Rezultatų pavyzdys Velčo (Welch) $t$ kriterijų taikant programa „R“ (variantas 1). Panašios formos rezultatai gaunami taikant ir kitus šiame skyriuje aprašomus kriterijus. Šiuo konkrečiu atveju lyginamas ląstelių terpių, kuriose yra skirtingas anglies šaltinis, optinis tankis (OD) ties 600 nanometrų. Laikoma, kad kuo OD didesnis, tuo terpėje daugiau ląstelių.

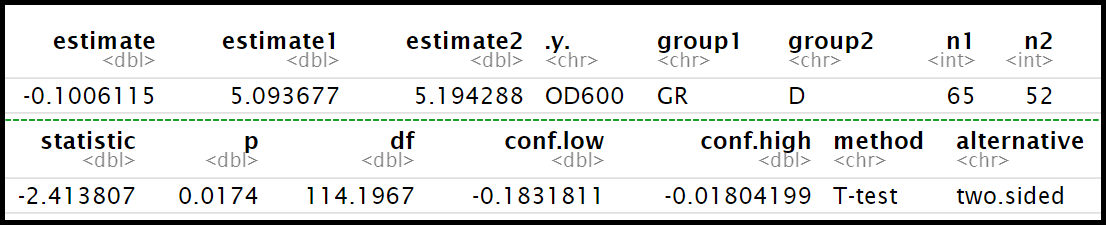
$Rezultatų pavyzdys Velčo (Welch) $t$ kriterijų taikant programa „R“ (variantas 2). Rezultatai tie patys, kaip pav. \@ref(fig:rez-ht-t-test), bet pateikti duomenų lentelės pavidalu. Žymėjimai: `.y.` -- analizuojamas kintamasis, `group1`, `group2` -- lyginamos grupės, `estimate` -- skirtumas tarp grupių vidurkių, `estimate1`, `estimate2` -- grupių vidurkiai, `n1`, `n2` -- grupių dydžiai, `statistic` -- kriterijaus ($t$) statistika, `p` -- p reikšmė, `df` -- skirstinio parametras (laisvės laipsniai), `conf.high`, `conf.low` -- skirtumo tarp grupių vidurkių pasikliautinųjų intervalų (95%) rėžiai, `alternative` -- alternatyvioji hipotezė (trumpas formulavimas), `method` -- trumpasis kriterijaus pavadinimas. Tai, jog naudojamas Velčo metodas, matome iš to, kad tirtos 2 grupės, o laisvės laipsniai užrašomi su trupmenine dalimi.$

Pav. 18.6: Rezultatų pavyzdys Velčo (Welch) $t$ kriterijų taikant programa „R“ (variantas 2). Rezultatai tie patys, kaip pav. 18.5, bet pateikti duomenų lentelės pavidalu. Žymėjimai: .y. – analizuojamas kintamasis, group1, group2 – lyginamos grupės, estimate – skirtumas tarp grupių vidurkių, estimate1, estimate2 – grupių vidurkiai, n1, n2 – grupių dydžiai, statistic – kriterijaus ($t$) statistika, p – p reikšmė, df – skirstinio parametras (laisvės laipsniai), conf.high, conf.low – skirtumo tarp grupių vidurkių pasikliautinųjų intervalų (95%) rėžiai, alternative – alternatyvioji hipotezė (trumpas formulavimas), method – trumpasis kriterijaus pavadinimas. Tai, jog naudojamas Velčo metodas, matome iš to, kad tirtos 2 grupės, o laisvės laipsniai užrašomi su trupmenine dalimi.

Tarp kompiuterinės programos rezultatų turėtumėte pamatyti:

metodo pavadinimą,
kriterijaus statistikos reikšmę (pvz., $t$, $U$, $V$ ar kita statistika),
parametriniams kriterijams – skirstinio parametrų reikšmes (pvz., laisvės laipsniai, df, parameter). Neparametriniams kriterijams šitokių dalykų įprastai nebūna,
$p$ reikšmę,
alternatyvos rūšį (vienpusės „daugiau už“, „mažiau už“ ar dvipusė „nelygu“).

Taip pat tarp rezultatų kartais galima rasti vidurkių reikšmes (pvz., estimate1, estimate2) ar skirtumo tarp vidurkių (estimate) pasikliautinuosius intervalus (conf.high, conf.low).

18.4.2 Rezultatų aprašymas: padėties lyginimas

Aprašydami rezultatus laikykitės „11.7 Rezultatų aprašymo principai“ skyriuje išdėstytų principų.

Pirmiausia, aiškiai nurodomas taikytas analizės metodas bei kompiuterinė programa, kuria atlikti skaičiavimai, ir tiksli jos versija, kai reikia, pacituojamas šaltinis, kuriame aprašytas metodas. Parametriniu atveju nurodomi visų grupių vidurkiai, neparametriniu – medianos. Rezultatai gali būti pateikti lentele. Grafiškai pateikiama kiekybiniams kintamiesiems tinkama diagrama pogrupiais (histograma, stačiakampė diagrama ar pan.) arba vidurkiai/medianos su pasikliautinaisiais intervalais (ar kitu neapibrėžties/paklaidų įvertinimo būdu).

Rezultatų aprašymo pavyzdys:
„Analizei naudotas programos R (versija 4.3.3) paketas rstatix (versija 0.7.2).“
„Lygintas dviejų terpių su ląstelėmis optinis tankis ties 600 nm. Skirtumas tarp terpės D (vidurkis 5,19, SD = 0,21, n = 52) ir terpės GR (vidurkis 5,09, SD = 0,24, n = 65) optinių tankių buvo statistiškai reikšmingas (Welch $t$, dvipusė alternatyva, $t$(114,20) = 2,41, $p$ = 0,017; vidurkių skirtumas yra 0,10, 95% PI 0,02–0,18, $d^*$ = 0,44, $\omega^2$ = 0,04).“

Informacijos šaltiniai

Albers C., Lakens D. When power analyses based on pilot data are biased: Inaccurate effect size estimators and follow-up bias, Journal of Experimental Social Psychology 74: 187–195 (2018). DOI: 10.1016/j.jesp.2017.09.004.

Čekanavičius V., Murauskas G. Statistika ir jos taikymai II. Vilnius: TEV (2004).

Durlak J.A. How to Select, Calculate, and Interpret Effect Sizes, Journal of Pediatric Psychology 34(9): 917–928 (2009). DOI: 10.1093/jpepsy/jsp004.

Ialongo C. Understanding the effect size and its measures, Biochemia Medica: 150–163 (2016). DOI: 10.11613/BM.2016.015.

Mordkoff J.T. A Simple Method for Removing Bias From a Popular Measure of Standardized Effect Size: Adjusted Partial Eta Squared, Advances in Methods and Practices in Psychological Science 2(3): 228–232 (2019). DOI: 10.1177/2515245919855053.

Tomczak M., Tomczak E. The need to report effect size estimates revisited. An overview of some recommended measures of effect size, Trends in Sport Sciences 21: 19–25 (2014). Prieiga per internetą: http://tss.awf.poznan.pl/files/3_Trends_Vol21_2014__no1_20.pdf.

Zimmerman D.W. A note on preliminary tests of equality of variances, Br. J. Math. Stat. Psychol. 57(1): 173–181 (2004). DOI: 10.1348/000711004849222.