19. Padėties lyginimas (kelioms imtims)
Tikslas – susipažinti su statistinių hipotezių apie skirstinių ar jų parametrų (pvz., vidurkių) padėtį tikrinimo būdais kelioms imtims taikant dispersinę analizę (ANOVA) ar jai analogiškus statistinius kriterijus. Skyriuje akcentuojamas nepriklausomų imčių atvejis.
19.1 ANOVA ir jos analogai
ANOVA yra trumpasis dispersinės analizės (angl. ANalysis Of VAriance) pavadinimas. Tai metodų šeima, skirta pagal dispersijas tikrinti, ar skirtumai tarp kelių grupių padėties (vidurkių) yra statistiškai reikšmingi. Tokio tipo analizės reikia nagrinėjant klausimus:
- ar kelių skirtingų irisų rūšių vidutiniai žiedlapių dydžiai skiriasi?
- ar kelių gydymo metodų efektyvumas skiriasi?
- kurią iš terpių geriausia naudoti kituose eksperimento etapuose (t.y., ar ląstelės, auginamos keliose skirtingose terpėse, yra linkusios būti skirtingo dydžio?);
- kurį pašarą iš 6 turimų naudoti efektyviausia norint didžiausių viščiukų?
Klasikinis ANOVA variantas (vienfaktorė nepriklausomų imčių ANOVA) – tai Stjudento \(t\) kriterijaus analogas, kai norima palyginti dviejų ar daugiau nepriklausomų imčių (grupių) vidurkius. Sakykime, kad lyginame \(k\) grupių. Nulinė analizės hipotezė teigia, kad visų grupių vidurkiai lygūs, o jos alternatyva – bent dviejų grupių (kurių tiksliai – pasakyti negalima) vidurkiai skiriasi:
Čia \(i\) ir \(j\) – lyginamų grupių numeriai.
Atlikdami ANOVA pagal dispersijas tikriname, ar skirtumai tarp vidurkių yra statistiškai reikšmingi. Jei norime patikrinti, ar skirtumai tarp dispersijų yra reikšmingi, naudojame, pvz., Levene (Livyno) kriterijų.
Atkreipkite dėmesį, kad yra keli ANOVA variantai. Kai nepriklausomų grupių lyginimas atliekamas pagal vieną kategorinį kintamąjį (t.y., pagal vieną faktorių), ANOVA vadinama vienfaktore (angl. one-way ANOVA arba one factor ANOVA). Jei pagal du – dvifaktorė (angl. two-way) ir t.t. (angl. multi-way arba tiesiog factorial ANOVA). Yra ir specialių ANOVA variantų, skirtų priklausomoms imtims, pvz., blokuotųjų duomenų ANOVA (angl. repeated measures ANOVA). Taip pat yra neparametrinių analogų, tokių kaip Kruskal-Wallis (Kruskalo-Voliso) kriterijus, kuris lygina nebe vidurkius, o tai, ar bent viena grupė yra linkusi turėti kitokias (didesnes arba mažesnes) reikšmes nei visos kitos. Šiuos metodus galima laikyti ankstesnio skyriaus metu nagrinėtų metodų generalizacijomis daugiau nei 2 imtims (lentelė 19.1).
| Savybės | Lygiai 2 grupės | Kelios (2 ar daugiau) grupės |
|---|---|---|
| Normalieji duomenys, lygios dispersijos | Stjudento \(t\) kriterijus nepriklausomoms imtims | Vienfaktorė nepriklausomų imčių ANOVA |
| Normalieji duomenys, dispersijos skirtingos | Welch \(t\) kriterijus | Welch \(F\) kriterijus (Welch ANOVA) |
| Neparametrinis kriterijus | Mann-Whitney-Wilcoxon | Kruskal-Wallis kriterijus |
Šiame skyriuje mokysimės taikyti tik vienfaktorės ANOVA modelį, skirtą nepriklausomoms duomenų imtims, bei šio modelio analogus, kurie gali būti taikomi, jei pažeidžiamos šio modelio prielaidos (pvz., normalumas ar dispersijų homogeniškumas).
19.2 Pasirinkimų schema
Vienfaktorė nepriklausomų imčių ANOVA (toliau vadinsime klasikiniu ANOVA variantu) grindžiama šiomis prielaidomis:
- Tiriamieji tarpusavyje nepriklausomi;
- Grupių duomenys yra nepriklausomi;
- Kiekvienos grupės kintamieji pasiskirstę normaliai (\(X_{gr} \sim \mathcal{N}(\mu_{gr},\sigma^2)\));
- Grupių dispersijos yra lygios.
Kai reikia rinktis iš šių 3 kriterijų ir tinka keli, mūsų prioritetai:
- vienfaktorė ANOVA (kai galima, teikiame pirmenybę);
- Welch \(F\) kriterijus;
- Kruskal-Wallis kriterijus (jei netinka kiti).
Prielaidos gali būti tikrinamos pagal pradinius (t.y., analizei parengtus) duomenis prieš sudarant ANOVA modelį, kaip tai daroma \(t\) ir kitų anksčiau nagrinėtų kriterijų atveju, arba, sudarius ANOVA modelį, pagal liekamąsias paklaidas, dar vadinamas likučiais (angl. errors arba residuals), kaip tai daroma tiesinės regresinės analizės atveju.
Schema yra supaprastinta ir tik rekomendacinio pobūdžio. Jos tikslas – būti „atspirties tašku“ renkantis analizės metodą. Konkrečiu atveju gali būti išlygų, papildomų sąlygų arba pasirinkimo variantų, kurie schemoje nepažymėti.
“.](fig/pic/10/schema-padetis-kelios-nepriklausomos-gr.png)
Pav. 19.1: Skirstinio padėties lyginimas kelioms imtims. Schema, padedanti išsirinkti reikiamą vienfaktorės nepriklausomų imčių (grupių) ANOVA variantą ar jos analogą. Apatinėje dalyje pateikiami keli galimi post-hoc analizės variantai, skirti grupes lyginti poromis. Skaičiais pažymėtų schemos dalių paaiškinimas pateiktas tekste žemiau. Spalvinio žymėjimo reikšmės pateiktos skyriuje „12.4 Schemos metodams pasirinkti“.
Skaičiais pažymėtų 19.1 schemos dalių paaiškinimai:
- Jei imčių (grupių) dydžiai vienodi arba beveik vienodi (t.y., subalansuoti), o imtys pakankamai didelės, ANOVA atspari mažiems ir net vidutinio dydžio normalumo ir lygių dispersijų prielaidų pažeidimams. Kuo imties dydis mažesnis ar kuo mažiau grupių dydžiai subalansuoti, tuo ANOVA jautresnė šių prielaidų pažeidimams.
- Sprendžiant „iš akies“, mažiausia ir didžiausia dispersijos (ne standartiniai nuokrypiai) neturėtų skirtis daugiau kaip 3 kartus (Čekanavičius ir Murauskas 2004, p.51).
- „Vienodos formos“ reiškia, kad visų grupių skirstinių asimetrija yra vienos krypties ir panašaus stiprumo, o sklaida (dispersijos) – daugmaž vienoda (pav. 19.2).
- Jei visų grupių skirstinių forma vienoda ir skiriasi tik poslinkio parametru, t.y., skiriasi tik skirstinio padėtis (tokiems duomenims ir rekomenduojamas Kruskal-Wallis kriterijus) tada galime daryti išvadas apie grupių medianas: tokiu atveju rezultatai informatyvesni nei 5 punkto atveju;
- Jei lyginamų grupių skirstinių forma skirtinga (skiriasi dispersijos, būdinga skirtingos krypties asimetrija), išvadas darome tik apie tai, kad bent viena grupė yra linkusi būti kitokia (arba didesnė, arba mažesnė) nei kitos. Techniškai kalbant, išvadas darome tik apie vidutinius rangus, bet ne apie medianas. Todėl šie rezultatai mažiau informatyvūs nei 4 punkto atveju. Be to, ir kriterijaus galia mažesnė.
- Apie galimus ANOVA post-hoc analizės variantus:
- Tukey HSD (angl. honestly significant difference) kriterijaus taikymui duomenys turi būti normalieji, dispersijos lygios, o imties dydžiai (beveik) vienodi. Jei bent viena iš pastarųjų prielaidų netenkinama, geriau naudoti Games-Howell kriterijų. Papildomos \(p\) reikšmių korekcijos nereikia, nes pats kriterijus ir yra korekcija.
- Games-Howell kriterijus yra Tukey HSD modifikacija, nereikalaujanti lygių dispersijų ar vienodų grupių dydžių. Visgi, normalumo sąlygos reikia. Kiekvienoje lyginamoje imtyje turi būti bent 6 nariai. Papildomos \(p\) reikšmių korekcijos nereikia, nes pats kriterijus ir yra korekcija.
- Galima atlikti keletą nepriklausomų imčių (Stjudento ar Welch) \(t\) kriterijaus taikymo procedūrų, bet būtina naudoti daugkartinių lyginimų \(p\) reikšmių korekcijos metodus (Holm, Bonferroni ar kitą procedūrą);
- Yra ir kitų čia nepaminėtų post-hoc kriterijų.
- Apie galimus Welch ANOVA post-hoc analizės variantus:
- Games-Howell (aprašyta punkte 6b);
- Galima keletą kartų taikyti Welch \(t\) kriterijų grupių poroms, bet būtina atlikti \(p\) reikšmių korekciją (žiūrėti punkte 6c);
- Yra kitų čia nepaminėtų kriterijų. Šie kriterijai privalo nereikalauti lygių dispersijų prielaidos.
- Games-Howell (aprašyta punkte 6b);
- Apie galimus Kruskal-Wallis kriterijaus post-hoc analizės variantus:
- Galima taikyti Conover-Iman, Dunn arba analogišką kriterijų. Nors Dunn kriterijus yra plačiau taikomas, tačiau Conover-Iman (apie kurį ilgą laiką buvo viešai nežinota) kriterijus yra galingesnis. Bet kuriuo atveju gautoms \(p\) reikšmėms reikia atlikti Holm, Bonferroni ar kitą daugkartinių lyginimų korekciją (jei statistinis paketas to neatlieka automatiškai).
- Jei jūsų programa minėtųjų kriterijų neturi, galima keletą kartų lyginamų grupių poroms taikyti nepriklausomų imčių Mann-Whitney-Wilcoxon kriterijų, bet tokiu atveju irgi būtina naudoti \(p\) reikšmių korekcijos metodus. Visgi, šis būdas nėra rekomenduojamas, kadangi kiekvieno lyginimo metu rangavimas vykdomas iš naujo;
- Yra ir kitų čia nepaminėtų kriterijų. Jie privalo būti neparametriniai ir nereikalauti normalumo.
- Tai schema 18.2 (ankstesniame skyriuje).
- Plačiau šioje svetainėje nenagrinėjama. Informacijos galite ieškoti nemokamame kurse „Comparing Multiple Means in R“ .
Jei imtys yra pakankamai didelės, o imčių didumai yra (daugmaž) vienodi, ANOVA yra ganėtinai atspari nedideliems ir netgi vidutinio dydžio nuokrypiams nuo normalumo ir lygių dispersijų (dispersijų homogeniškumo) prielaidų.
{target="_blank"} (Copyright 2014. Laerd Statistics).](https://statistics.laerd.com/stata-tutorials/img/kwht/different-distributions-location-stochastic.png)
Pav. 19.2: Panašios formos skirstiniai, kurie skiriasi tik poslinkio parametru, (kairėje) ir skirtingos formos skirstiniai (dešinėje). Skirstinio forma lemia, kokio tipo išvadas galime daryti: apie medianas ar apie padėtį bendrai. Šaltinis (Copyright 2014. Laerd Statistics).
19.3 Išsamios ANOVA analizės aspektai
19.3.1 Eiga
Jei reikia atlikti ANOVA ar į ją panašią analizę, rekomenduojama tokia eiga:
- Tiksliai apsibrėžiamas klausimas, suformuluojamos hipotezės;
- Atliekama išsami duomenų suvestinė ir nubraižomas grafikas (pvz., pav. 19.3), galintis padėti atsakyti į iškeltą klausimą;
- Patikrinamos analizės prielaidos ir reikalavimai, ar galima naudoti ANOVA:
- tiriamieji tarpusavyje turi būti nepriklausomi, kitaip šio skyriaus metodai bus netinkami. Reikės naudoti daugiapakopius (angl. multilevel) metodus.
- ar duomenų grupės nepriklausomos (ar matavimai nėra kartotiniai):
- sprendžiame pagal tai, kaip buvo suplanuotas ir atliktas eksperimentas.
- kitu atveju pasirenkami priklausomoms imtims tinkami metodai.
- ar duomenų pakankamai daug:
- geriausia, kai kiekvienoje grupėje bent po 15, jei grupių daug – bent po 20 atvejų;
- kitu atveju duomenys privalo skirstytis idealiai normaliai, grupių dispersijos tik nežymiai skirtis;
- jei duomenų per mažai, negalime patikimai patikrinti parametriniams kriterijams keliamų (normalumo ir lygių dispersijų) prielaidų,
- būdas „apeiti“ mažų imties dydžių problemą – prielaidas tikrinti pagal liekamąsias paklaidas.
- normalumo prielaida:
- Galima tikrinti pagal liekamąsias paklaidas (tiesinio modelio diagnostikos grafikai, Shapiro-Wilk kriterijus likučiams). Jei nesimato nukrypimų nuo normaliojo pasiskirstymo, teigiame, kad prielaida tenkinama. Kitu atveju galime tikrinti taip, kaip aprašyta kitame punkte;
- Tikrinant pagal pradinius (analizei parengtus) duomenis, normalumas turi būti tenkinamas kiekvienai grupei atskirai. Svarbu, kad grupių dydžiai būtų pakankamai dideli.
- Jei prielaida netenkinama, taikomi neparametriniai metodai.
- lygių dispersijų prielaida:
- Galima tikrinti pagal liekamąsias paklaidas (tiesinio modelio diagnostikos grafikai, Breush-Pagan kriterijus);
- Galima tikrinti pagal pradinius (analizei parengtus) duomenis (Levene/Brown-Forsythe kriterijai);
- Jei pažeista lygių dispersijų, bet tenkinama normalumo sąlyga, naudojamas Welch \(F\) kriterijus.
- Teisingai pasirenkama ir atliekama pagrindinė analizė.
- Tikrinamas statistinis reikšmingumas;
- Skaičiuojamas bendrasis efekto dydis (pvz., \(\omega^2\) ar pan.).
- Jei pagrindinės analizės rezultatas statistiškai reikšmingas (rodo, kad bent viena grupė nuo kitų skiriasi statistiškai reikšmingai, bet nepasako kuri), atliekama papildoma post-hoc analizė (poriniai palyginimai norint išsiaiškinti, kurios konkrečiai grupės skiriasi).
- Galima atlikti lyginimus „kiekvienas su kiekvienu“ (daugiau lyginimų, bet mažesnė galia) arba „kiekvienas su kontrole“ (mažiau lyginimų, bet kartais to užtenka, nes atliekama tik dalis galimų lyginimų). Apie tai, kurį variantą pasirinkti, sprendžiame tyrimo planavimo etape, o ne tada, kai įsikeliame duomenis į kompiuterį ir pamatome grafiką.
- Tiriamas statistinis reikšmingumas, vengiant pernelyg padidėjusios I rūšies klaidos tikimybės, taikoma \(p\) reikšmių korekcija.
- Kiekvienai porai skaičiuojamas efekto dydis.
- Rezultatai aprašomi.
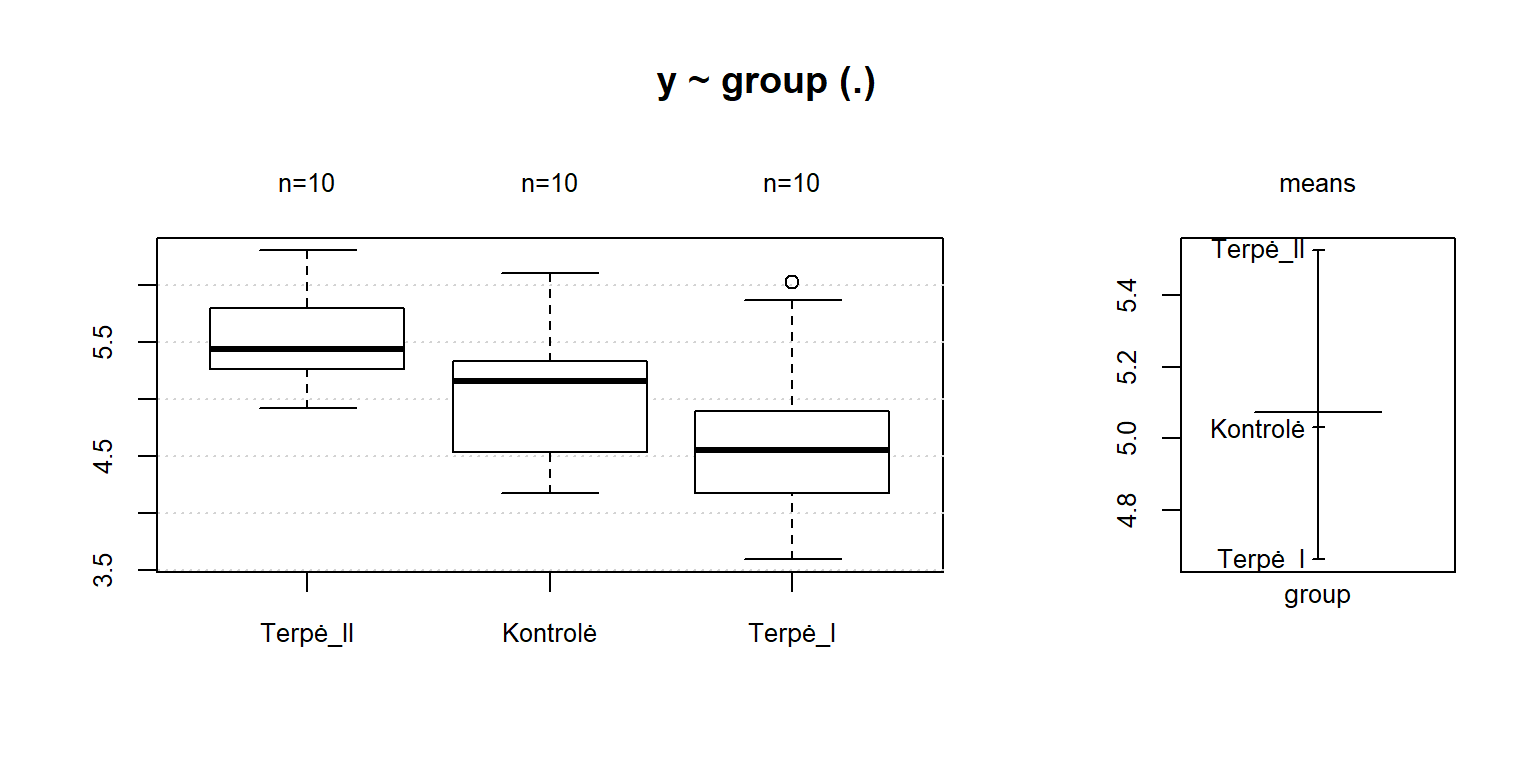
Pav. 19.3: Dispersinei analizei tinkamų duomenų pavyzdys. Grupės išdėliotos mažėjimo tvarka pagal grupės medianą.
Apie grafikų interpretaciją rašoma skyriuje „5.3.3 Grafinis grupių palyginimas.“
19.3.2 Prielaidų tikrinimas: normalumas ir dispersijų homogeniškumas
Dispersinės analizės normalumo ir homoskedastiškumo (lygių dispersijų) prielaidas galima tikrinti dviem būdais (matyt, geriausia abu ir naudoti):
- Tikrinimas pagal pradinius duomenis, kaip tai įprastai atliekama statistiniams kriterijams (skaitykite skyriuje „16 Normalumo tikrinimas“ bei „17 Sklaidos lyginimas“):
- normaliojo pasiskirstymo prielaidą turėtų tenkinti kiekviena grupė atskirai.
- ANOVA ir regresinė analizė yra tiesinių modelių (angl. linear models) rūšys. Todėl ANOVA normalumo prielaidą galima tikrinti ir pagal liekamąsias paklaidas (apie šį būdą taip pat bus rašoma skyriuje „21 Tiesinė regresija“. Liekamosios paklaidos (angl. errors) dar vadinamos likučiais (angl. residuals). ANOVA (arba t kriterijaus) atveju jos apskaičiuojamos iš taško vertės atimant grupės, kuriai tas taškas priklauso, vidurkį (t.y, skaičiuojamos kiekvienam taškui atskirai: kiek yra duomenų taškų, tiek yra ir likučių). Likučių išsidėstymas turi būti normalusis ir homoskedastiškas (t.y., būti tenkinama lygių dispersijų prielaida). Prielaidų tikrinimas atliekamas pagal tiesinio modelio diagnostikos (prielaidų tikrinimo) grafikus (pav. 19.4, 19.5) bei naudojant likučių analizei skirtus statistinius kriterijus:
- normalumui – Shapiro-Wilk kriterijus (tik bus viena p reikšmė, nes visi likučiai analizuojami kartu).
- lygių dispersijų (homoskedastiškumo) prielaidai – Breush-Pagan kriterijus (o ne Levene/Brown-Forsythe)
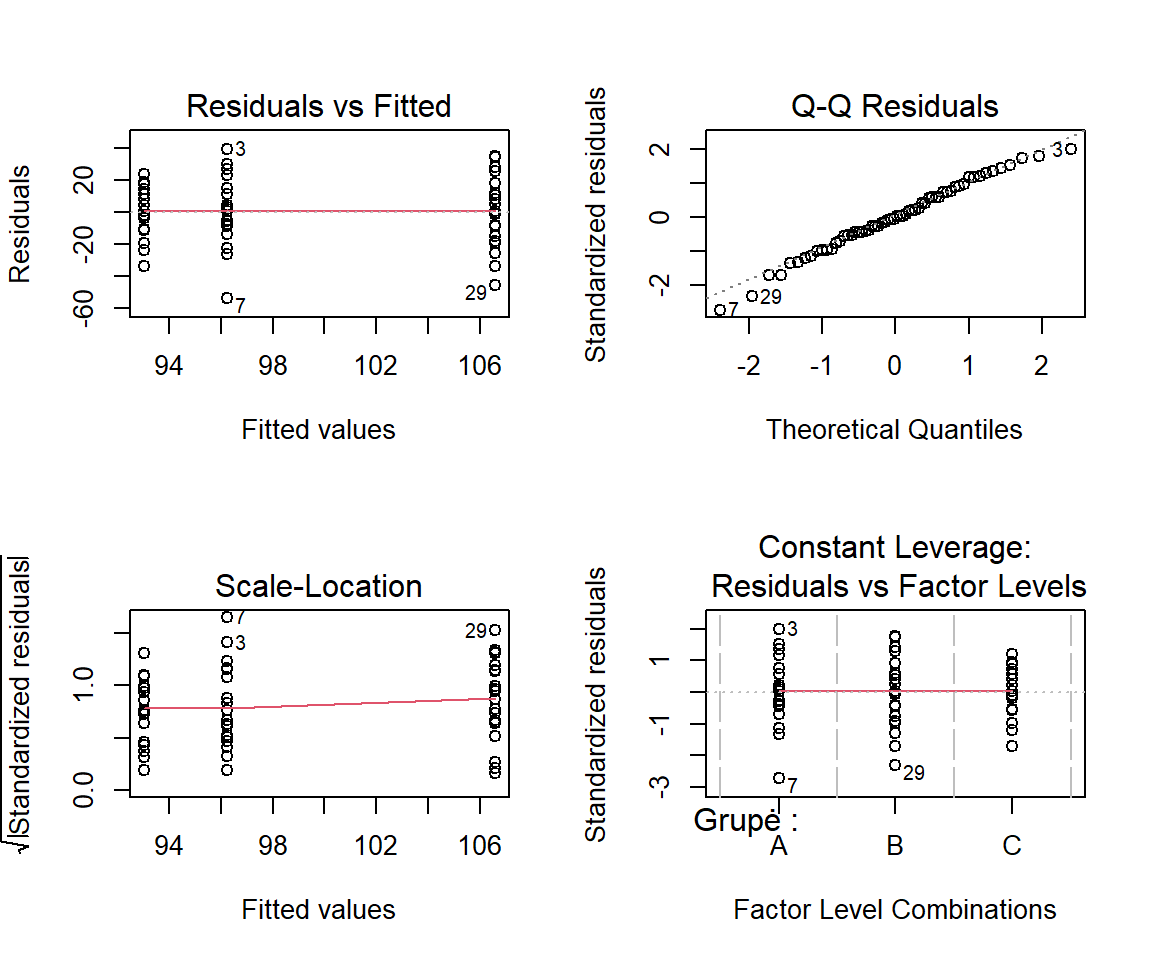
Pav. 19.4: ANOVA diagnostikos grafikai: prielaidos tenkinamos. Simuliuoti duomenys, paimti iš visiškai normaliai pasiskirsčiusių generalinių aibių, kurių dispersijos yra lygios. Kiekvienos grupės dydis \(n_i\) = 20. Grafikų paaiškinimai žemiau.
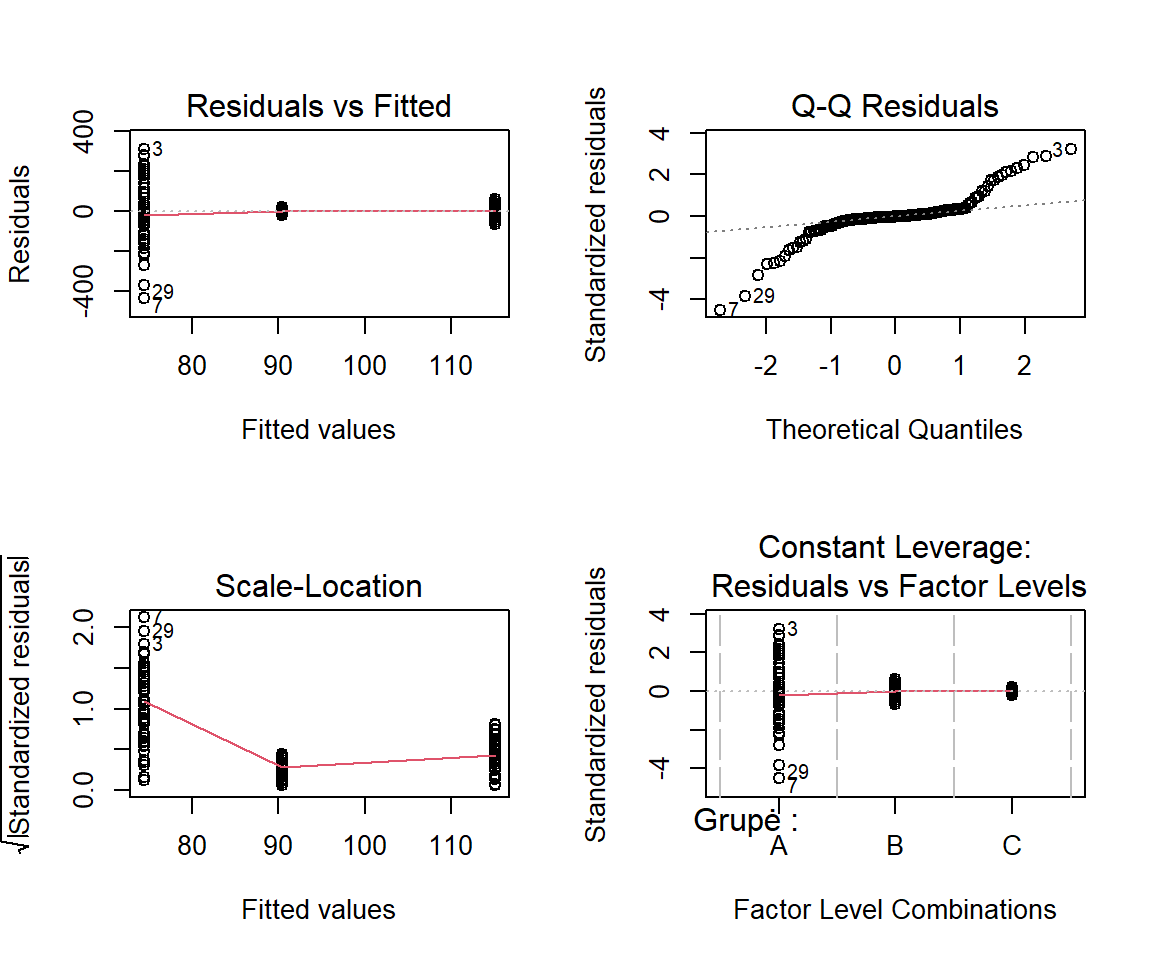
Pav. 19.5: ANOVA diagnostikos grafikai: pažeista lygių dispersijų prielaida, likučių pasiskirstymas nėra normalusis. Simuliuoti duomenys, paimti iš visiškai normaliai pasiskirsčiusių generalinių aibių, kurių dispersijos smarkiai skiriasi. Grupių dydžiai \(n_i\) = 50. Besiskiriančias dispersijas vaizduoja „Residuals vs Fitted“ (skiriasi taškų išsibarstymo aukštis) ir Scale-Location (per grupių centrus einanti linija nėra lygiagreti x ašiai) grafikai. Taip pat matome, kad dėl skirtingo dydžio dispersijų QQ grafike likučių pasiskirstymas tampa nebe normalusis. Tad pravartu normalumo prielaidą patikrinti kiekvienai grupei atskirai nubraižant QQ diagramą.
Lygių dispersijų prielaidos tikrinimas pagal tiesinio modelio diagnostikos grafikus:
- „Residuals vs. Fitted“ („paklaidos pagal prognozuojamas reikšmes“) grafikas. Jei prielaida tenkinama, visos taškų grupės pasižymi daugmaž vienoda sklaida, t.y., taškų išsibarstymo aukštis kiekvienoje taškų grupėje yra panašus (ar skiriasi mažiau nei 2-3 kartus).
- „Scale-Location“ (sklaidos-padėties) grafikas. Jei prielaida tenkinama, visų taškų grupių sklaida yra panašaus dydžio, o tendencijos linija – daugmaž lygiagreti x ašiai. Jei matomas aiškus tendencijos linijos nukrypimas nuo lygiagretumo (aiškus kitimas, leidimasis ar kitoks „raitymasis“), tada prielaida pažeista.
Normalumo tikrinimas:
- „Normal Q-Q“ grafikas. Jei prielaida tenkinama, visi taškai turi būti išsidėstę į maždaug vieną liniją ties įstrižaine.
- Jei dispersijos skiriasi smarkiai, tai paklaidos taip pat gali būti pasiskirsčiusios ne normaliai. Tokiu atveju pravartu normalumo prielaidą patikrinti kiekvienai grupei atskirai nubraižant QQ diagramą ir pasirinkti tinkamą ANOVA analogą.
Apie diagnostikos grafikus taip pat rašoma šiuose šaltiniuose:
19.3.3 Kelių grupių lyginimas: rezultatų pateikimas
Atlikdami post-hoc analizę, kelias grupes lyginame poromis. Lyginant kelias grupes, rezultatai gali būti pateikti kiekvienai lyginamai grupių porai atskiroje eilutėje. Tai patogu tik tada, kai grupių nedaug, nes lyginimų poromis (kiekvienas su kiekvienu) skaičius yra \(k(k-1)/2\) (\(k\) – grupių skaičius).
Žemiau esančiame pavyzdyje pateiktas trijų grupių palyginimas. Jame \(p\) reikšmė žymima Pr(>|t|), \(t\) statistika t value, o Terpė_I - Kontrolė == 0 rodo, kad lygintos grupės yra Terpė_I ir Kontrolė. Statistinis reikšmingumas žymimas žvaigždutėmis:
Pairwise comparisons using Conover's all-pairs test
data: y by group
P value adjustment method: holm
H0
t value Pr(>|t|)
Terpė_I - Kontrolė == 0 -1.267 0.215966
Terpė_II - Kontrolė == 0 1.915 0.132301
Terpė_II - Terpė_I == 0 3.182 0.010983 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Kai grupių daug, rezultatus patogiau pateikti kaip \(p\) reikšmių matricą:
Pairwise comparisons using Conover's all-pairs test
data: y by group
Kontrolė Terpė_I
Terpė_I 0.216 -
Terpė_II 0.132 0.011
P value adjustment method: holmČia matome, kad \(p\) reikšmė tarp Terpė_I ir Terpė_II lygi 0,011.
Visgi, jei grupių tikrai labai daug (sakykime – 8), net ir turint tokią matricą, sunku greitai ir efektyviai apibendrinti visus rezultatus: kurios grupės tarpusavyje skiriasi, o kurios ne?
A B C D E F G
B 1.00000 - - - - - -
C 0.00329 0.05921 - - - - -
D 7.7e-05 0.00248 1.00000 - - - -
E 6.1e-09 3.1e-07 0.00535 0.11261 - - -
F 5.0e-10 2.6e-08 0.00072 0.02156 1.00000 - -
G 2.3e-10 1.2e-08 0.00036 0.01237 1.00000 1.00000 -
H 6.2e-13 3.0e-11 1.1e-06 7.7e-05 0.11880 0.49213 0.65072Todėl yra efektyvesnis būdas parodyti skirtumus – cld. Jis aptariamas kitame poskyryje.
19.3.4 Kompaktiškas raidinis žymėjimas (cld)
Sakykime, kelias grupes lyginame poromis. Statistiškai reikšmingus rezultatus tarp grupių, kai lyginimų daug, galime pažymėti taip vadinamu kompaktišku raidiniu žymėjimu (angl., compact letter display, cld). Šio žymėjimo esmė: kiekvienai grupei suteikiama viena ar keletas raidžių. Interpretacija: tarp grupių, kurios neturi bendros raidės, skirtumai yra statistiškai reikšmingi. Jei grupės turi bent vieną bendrą cld raidę – skirtumai statistiškai nereikšmingi. Raidinis žymėjimas labai patogus, kai vienu metu poromis lyginame daug grupių.
| Grupė | cld | Sulygiuotas cld |
|---|---|---|
| Kontrolė | ab | ab |
| Terpė_I | a | a_ |
| Terpė_II | b | _b |
Lentelėje 19.2 rodoma, kad (su reikšmingumo lygmeniu \(\alpha = 0{,}05\)) statistiškai reikšmingi skirtumai yra tik tarp grupių „Terpė_I“ ir „Terpė_II“, nes jos neturi bendros raidės. Tuo tarpu reikšmingų skirtumų tarp kontrolės ir kitų grupių nėra, nes jos turi po vieną bendrą cld raidę.
Nėra bendros cld raidės – vadinasi, skirtumai statistiškai reikšmingi (su pasirinktu \(\alpha\)).
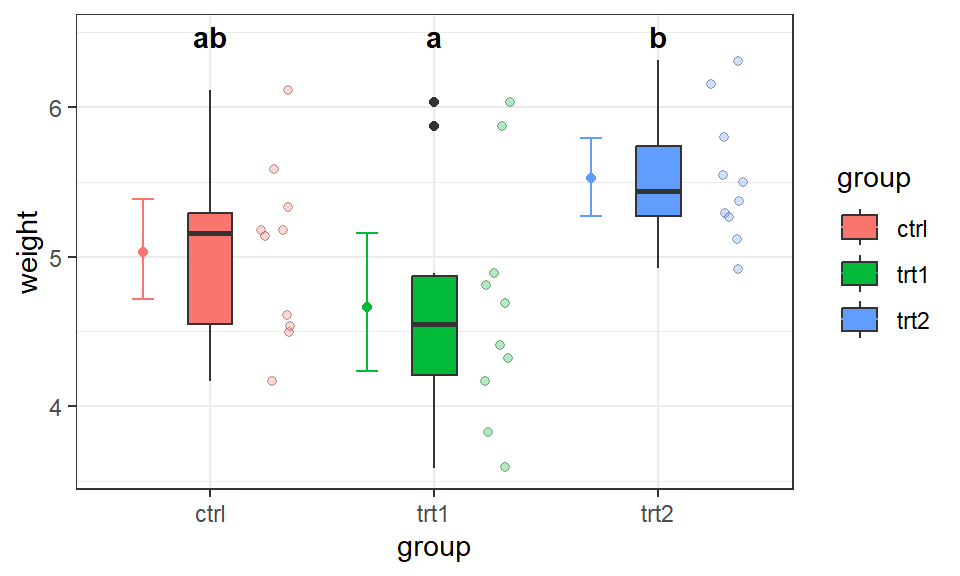
Pav. 19.6: Kompaktiškas raidinis žymėjimas grafike.
Palyginkite praeitame skyrelyje pateiktą 8 lyginamų grupių (A-H) matricą su šia cld reikšmių lentele:
group cld spaced_cld
1 A a a____
2 B ab ab___
3 C bc _bc__
4 D cd __cd_
5 E de ___de
6 F e ____e
7 G e ____e
8 H e ____eKurios iš šių grupių statistiškai reikšmingai skiriasi, o kurios ne?
19.4 Efekto dydis
Jei turime daugiau nei 2 grupes, tada gali būti skaičiuojamas bendrasis \(r^2\) tipo efekto dydis (grupių skirtumais paaiškintos dispersijos dalis). Toliau tęsiant analizę, grupės gali būti lyginamos poromis ir skaičiuojami grupių poroms skirti efekto dydžiai (žr., skyrių 18.3).
Nepaisant to, kokia \(p\) reikšmė buvo gauta, tyrėjai privalo tarp rezultatų pateikti ir efekto dydį (Durlak 2009).
19.4.1 Nestandartizuotieji efekto dydžiai
Bendrasis (visoms grupėms iš karto) efekto dydis kintamojo matavimo vienetais nėra skaičiuojamas. Tačiau parametriniams metodams gali būti apskaičiuotas skirtumas tarp dviejų grupių vidurkių bei skirtumo pasikliautinasis intervalas. Taip pat kartais skaičiuojamas skirtumas tarp grupės vidurkio ir bendro visos duomenų imties vidurkio. Bet šiuo atveju, jei imties dydžiai nesubalansuoti, rezultatai gali būti iškreipti (kuo grupė santykinai didesnė už kitas, tuo jos vidurkis bus panašesnis į bendrą visų grupių vidurkį).
Taip pat galima išvardinti visų grupių vidurkius (parametriniu atveju) arba medianas (neparametriniu atveju) ir skirtumus leisti apsiskaičiuoti pačiam skaitytojui.
19.4.2 Standartizuotieji efekto dydžiai
Įprastai vienfaktorėje ANOVA analizėje bendras efekto dydis matuojamas kaip \(\eta^2\) (eta kvadratu) ir \(\omega^2\) (omega kvadratu) koeficientai: \(\eta^2\) laikomas paslinktuoju, o \(\omega^2\) – nepaslinktuoju (ar bent jau mažiau paslinktuoju) įverčiu, todėl \(\omega^2\) yra tikslesnis (Čekanavičius ir Murauskas 2004, p.74). Kai kategorinio kintamojo reikšmės yra manipuliuotos (t.y., eksperimentiniams tyrimams), o ne išmatuotos, koeficientas \(\omega^2\) gali būti apskaičiuotas pagal (19.1) lygtį (Albers ir Lakens 2018). Apie kitų koeficientų skaičiavimą informacijos galite rasti minėtame straipsnyje arba šioje svetainėje .
\[\begin{equation} \omega^2 = \frac{(F-1)\cdot\nu_{skaitiklio}}{F \cdot \nu_{skaitiklio}+\nu_{vardiklio}+1} \tag{19.1} \end{equation}\]Čia \(F\) – kriterijaus statistika, \(\nu\) laisvės laipsniai.
Koeficientai \(\omega^2\) ir \(\eta^2\) yra skirtingai skaičiuojami to paties dydžio įverčiai.
Koeficientai \(\omega^2\) ir \(\eta^2\) interpretuojami taip: kurią dalį duomenų sklaidos lemia grupių skirtumai (Čekanavičius ir Murauskas 2004, p.71), t.y., kuri priklausomo kintamojo dispersijos (sklaidos) dalis paaiškinama nepriklausomų kintamųjų reikšmėmis (0 – paaiškinta 0%, 1 – paaiškinta 100%). Preliminariai kalbant, efektą vertinti galima taip: 0,01 mažas, 0,06 – vidutinis, 0,14 – didelis (Field ir kt. 2012, p.455) ar \(\omega^2\) > 0,15 – pakankamai didelis (Čekanavičius ir Murauskas 2004, p.74). Tikslesnė interpretacija priklauso nuo mokslo šakos ir tyrimo pobūdžio. Tad geriausia šiuos dydžius lyginti su savo srities tyrėjų darbais.
Kruskalo-Voliso analizei gali būti skaičiuojamas koeficientas \(\eta_H^2\), kuris taip pat traktuojamas kaip nepriklausomu kintamuoju paaiškinta sklaidos dalis. Arba koeficientas \(E^2_H\) (epsilon kvadratu), kuris interpretuojamas kaip koreliacijos koeficientas (0 – ryšio nėra, 1 – idealus ryšys). Daugiau matematinių detalių straipsnyje (Tomczak ir Tomczak 2014).
Post-hoc analizei efekto dydžiai gali būti skaičiuojami 18.3 skyriuje nagrinėjamais metodais.
19.5 Rezultatų aprašymas
Aprašydami rezultatus laikykitės principų, pateiktų skyriuje „11.7 Rezultatų aprašymo principai“.
Parametriniai metodai – klasikinė ANOVA ir Welch \(F\) kriterijus – lygina duomenų vidurkius (vidurkis yra normaliojo skirstinio parametras), todėl aprašant šios analizės rezultatus reikia nurodyti grupių vidurkius. Tuo tarpu Kruskal-Wallis kriterijus yra neparametrinis, bendresnis ir lygina, ar duomenų skirstiniai pagal savo padėtį skiriasi, t.y., ar bent viena grupė yra linkusi būti mažesnė arba didesnė už kitas. Aprašant Kruskal-Wallis analizės rezultatus nurodomos visų grupių medianos. Jei grupių daug – vidurkiai/medianos nurodomi lentele. Išsamiame aprašyme taip pat nurodomas kriterijaus pavadinimas, kriterijaus statistika, parametrai, efekto dydis, \(p\) reikšmė ir bendras imties dydis. Geriausia, jei būtų pateikiamas ir grupių palyginimo grafikas.
19.5.1 ANOVA rezultatai
Aprašyme pateikiamas tikslus taikytos analizės pavadinimas, kriterijaus statistika \(F\) įprastai 2 skaitmenų po kablelio tikslumu, abu jos laisvės laipsniai (tiek skaitiklio, angl. numerator, tiek vardiklio, angl. denominator) ir \(p\) reikšmė 3-4 skaitmenų po kablelio tikslumu.
Pvz.:
Df Sum Sq Mean Sq F value Pr(>F)
group 2 3.766 1.8832 4.846 0.0159 *
Residuals 27 10.492 0.3886
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1- \(F\) statistika (
F value=4.846) - \(F\) skirstinio parametrai (
Df,2,27) - \(P\) reikšmė (
Pr(>F)=0.0159).
Stulpelyje Df pateikti laisvės laipsniai, F value – \(F\) statistika, Pr(>F) – \(p\) reikšmė. Šių rezultatų aprašymo pavyzdys:
„Skirtumai tarp grupių vidurkių buvo statistiškai reikšmingi (ANOVA, \(F(2; 27) = 4{,}85\), \(p = 0{,}016)\). Grupių vidurkiai pateikti lentelėje (nurodome lentelės numerį)“.
Papildomai reiktų nurodyti grupių vidurkius ir, geriausia, pateikti grafiką su grupių palyginimu.
19.5.2 Welch ANOVA rezultatai
Welch ANOVA rezultatų pavyzdys:
One-way analysis of means (not assuming equal variances)
data: y and group
F = 5.181, num df = 2.000, denom df = 17.128, p-value = 0.01739One-way analysis of means (not assuming equal variances)
data: fscore and fcategory
F = 90.59, num df = 2.000, denom df = 25.563, p-value = 0.000000000002494Čia F – \(F\) statistika, \(F\) skirstinio parametrai num df – skaitiklio laisvės laipsniai, denom df – vardiklio laisvės laipsniai (įprastai 2 skaitmenų po kablelio tikslumu), p-value – \(p\) reikšmė (3, kartais 4 skaitmenų po kablelio tikslumu). Tad analizės rezultatai turėtų būti apibūdinti taip:
„(Welch \(F\) kriterijus, \(F(2; ~25{,}56) = 90{,}59\), \(p < 0{,}001\))“.
Aprašydami rezultatus:
- Įprastai \(p\) reikšmę užrašome 3 skaitmenų po kablelio tikslumu.
- Visus kitus apvalintinus skaičius – 2 skaitmenų po kablelio tikslumu.
19.5.3 Kruskal-Wallis analizės rezultatai
Aprašant neparametrinio Kruskal-Wallis kriterijaus rezultatus pateikiamas kriterijaus pavadinimas, kriterijaus statistika \(\chi^2\), naudotino \(\chi^2\) skirstinio laisvės laipsniai, imties dydis \(n\) bei \(p\) reikšmė 3-4 skaitmenų po kablelio tikslumu. Jei \(p\) reikšmė labai maža, tai ją rašome maždaug taip \(p < 0{,}001\) ar \(p < 0{,}0001\). Pvz.:
Kruskal-Wallis rank sum test
data: y by group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842Kruskal-Wallis rank sum test
data: Ozone by Month
Kruskal-Wallis chi-squared = 29.267, df = 4, p-value = 0.000006901Aprašymas turėtų atrodyti maždaug taip:
„Skirtumai tarp grupių buvo statistiškai reikšmingi (Kruskal-Wallis kriterijus, \(\chi^2(4; n = 153) = 29{,}27\), \(p < 0{,}001\)). Grupių pasiskirstymas vaizduojamas grafike (nurodome grafiko numerį), skaitinės suvestinės pateiktos lentelėje (nurodome lentelės numerį)“.
Reikšmė chi-squared nurodo \(\chi^2\) statistiką, df – \(\chi^2\) skirstinio parametrą pavadinimu „laisvės laipsniai“, n = 153 – imties dydį, p-value – \(p\) reikšmę. Papildomai turėtų būti pateiktos visų grupių medianos ir, geriausia, grafikai.
19.5.4 Post-hoc analizės rezultatai
Jei atlikta post-hoc analizė, jos rezultatai taip pat aprašomi, ir tai daroma panašiai kaip ir \(t\) ar Wilcoxon kriterijų aprašymo atvejais. Tiksliai apibūdinamas ir analizės metodas, ir \(p\) reikšmių korekcijos metodas (jei jis taikytas). Nurodoma, kurių būtent porų lyginimo rezultatas pateikiamas (visų tarpusavyje, visų su kontrole ar pan.). Jei rezultatų daug – jie gali būti pateikiami lentele. Rekomenduoju naudoti cld žymėjimus (skyrelis 19.3.4) ir paaiškinti, ką tie žymėjimai reiškia. Taip pat galima nurodyti standartizuotuosius efekto dydžius.
Tukey HSD kriterijaus rezultatų pavyzdys
Rezultatų pavyzdys, kuriuos gali pateikti statistinės analizės programos:
diff ci.lo ci.hi t df p
Terpė_I-Kontrolė -0.371 -1.062 0.32 1.33 27 .391
Terpė_II-Kontrolė 0.494 -0.197 1.19 1.77 27 .198
Terpė_II-Terpė_I 0.865 0.174 1.56 3.10 27 .012
Žymėjimai:
diff– skirtumas tarp grupių vidurkių;ci.lo– apatinis skirtumo pasikliautinojo intervalo (PI) rėžis;ci.hi– viršutinis skirtumo PI rėžis;t– \(t\) statistika;df– \(t\) skirstinio parametras – laisvės laipsniai;p– porinio lyginimo \(p\) reikšmė.
Kartais nuliai prieš tašką nerašomi \((p = .391).\) Tai privalomas reikalavimas tokiose mokslo šakose kaip psichologija.
Games-Howell kriterijaus rezultatų pavyzdys
Rezultatų pavyzdys, kuriuos gali pateikti statistinės analizės programos:
diff ci.lo ci.hi t df p
Terpė_I-Kontrolė -0.371 -1.172 0.43 1.19 16.5 .475
Terpė_II-Kontrolė 0.494 -0.101 1.09 2.13 16.8 .113
Terpė_II-Terpė_I 0.865 0.114 1.62 3.01 14.1 .024Žymėjimai analogiški kaip ir Tukio HSD analizės atveju. Pagrindinis skirtumas – laisvės laipsniai su trupmenine dalimi.
19.6 Priklausomų imčių, faktorinė ir kiti ANOVA variantai
Mes apžvelgėme tik kelis dažniausiai naudojamus ANOVA variantus nepriklausomoms imtims. Jei jūs turite kartotinius matavimus (priklausomas imtis), kelis kategorinius kintamuosius (kelių faktorių eksperimentai), jums reikalinga kitokio ANOVA tipo analizė ar jos analogai. Rekomenduoju nemokamą kursą „Comparing Multiple Means in R“ . Kursą sudaro 7 temos, kuriose nuosekliai paaiškinama, kaip nuodugniai atlikti dominančią analizę.