7. Skirstinių taikymas uždaviniams spręsti
Šiame skyriuje bus supažindinta, kaip sprendžiami tikimybiniai uždaviniai.
Bendrosios rekomendacijos, kaip spręsti tikimybinius uždavinius, kurių sprendimui naudojami skirstiniai:
- Pirmiausia pagal uždavinio sąlygą reikia nuspręsti, ar uždaviniui spręsti apskritai reikalingas skirstinys.
- Jei taip, tada reikia nustatyti, ar atsitiktinis dydis yra tolydusis, ar diskretusis, bei koks galėtų būti jo skirstinio tipas ir parametrai.
- Po to spręsti, kas duota (kvantilis, konkreti reikšmė ar tikimybė) bei ką reikia apskaičiuoti (kvantilį, konkrečią reikšmę, reikšmių intervalą, tikimybę ar kokią nors kitą skirstinio savybę, pvz., vidurkį).
- Tada nuspręsti, ar naudoti tikimybių skaičiuokles, ar užtenka kurių nors formulių, aprašančių skirstinio savybes, pvz., vidurkį.
- Galiausiai, svarbu patikrinti, ar rezultatas yra logiškas.
7.1 Uždavinių sprendimo principai
Tikimybinius uždavinius, kuriems spręsti naudojami skirstiniai, įprastai galima suskirstyti į vieną iš kelių uždavinių tipų, kuriuos dabar ir aptarsime. Šiuos uždavinius galime spręsti naudodamiesi statistikos vadovėlių prieduose esančiomis lentelėmis, programa „R“, papildiniu „R Commander“ arba programos „GeoGebra“ tikimybių skaičiuokle.
7.1.1 Žinome tikimybę, kaip rasti kvantilį?
- Nustatome, su kokio tipo ats.d. susidūrėme:
- tolydžiuoju ar diskrečiuoju.
- Pasirenkame tinkamą teorinio modelio (skirstinio) tipą:
- normalųjį, Puasono, binominį ar kitą.
- Apskaičiuojame modelio parametrus:
- jie gali būti nurodyti uždavinio sąlygoje.
- Nurodome tikimybę (skaitine išraiška);
- Pažymime, kuri tai tikimybė:
- Tikimybė „mažiau už“ (α, „lower tail“) ar
- Tikimybė „daugiau už“ (1-α, „upper tail“).
- Naudodami skaičiuoklę ar funkciją apskaičiuojame kvantilį (konkretų skaičių).
Pavyzdys, kaip galime užrašyti tokio tipo uždavinio sąlygą: „jei \(X \sim\mathcal{B}(n = 25; p = 0{,}2)\) ir \(P(X<k)=0{,}22\), tai kam lygus \(k\)?“
Užduotis 7.1
- Ar tiesa, kad:
- …kai Puasono skirstinio parametras \(\lambda = 3\), tai skirstinio kvantilis, atitinkantis tikimybę \(\alpha=0.5\), yra lygus 6?
- …kai geometrinio skirstinio sėkmės tikimybė (skirstinio parametras) \(p = 1\), tai kvantilis, atitinkantis tikimybę \(1-\alpha=0.4\) yra lygus 4.
7.1.2 Žinome kvantilį, kaip rasti tikimybę?
- Nustatome, su kokio tipo ats.d. susidūrėme:
- tolydžiuoju ar diskrečiuoju.
- Pasirenkame tinkamą teorinio modelio (skirstinio) tipą:
- normalųjį, Puasono, binominį ar kitą.
- Apskaičiuojame modelio parametrus:
- jie gali būti nurodyti uždavinio sąlygoje.
- Nurodome kvantilį (skaitine išraiška);
- Pažymime, kuri tikimybė mus domina:
- Tikimybė „mažiau už“ (α, „lower tail“) ar
- Tikimybė „daugiau už“ (1-α, „upper tail“).
- Naudodami skaičiuoklę ar funkciją apskaičiuojame tikimybę (skaičių tarp 0 ir 1).
Pavyzdys, kaip galime užrašyti tokio tipo uždavinio sąlygą: „jei \(X \sim\mathcal{B}(n = 25; p = 0{,}2)\), tai kam lygi tikimybė \(P(X<9)\)?“
Jei mums reikia apskaičiuoti tikimybę, kad reikšmė patenka į intervalą, tada galime naudoti pav. 7.1 vaizduojamą principą.
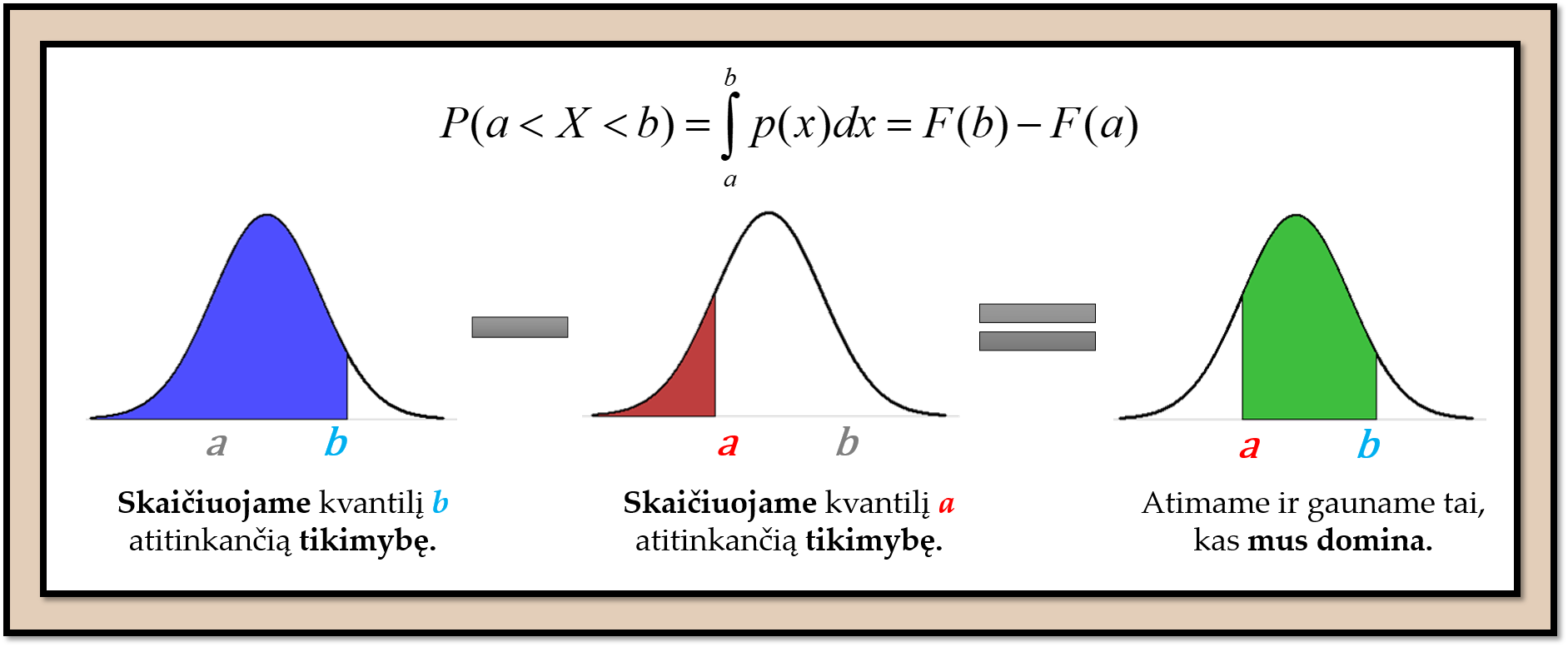
Pav. 7.1: Principas, kaip apskaičiuoti tikimybes, kad reikšmė pateks į intervalą.
Užduotis 7.2
- Kokia tikimybė, kad reikšmė, atsitiktinai pasirinkta iš Stjudento \(\mathcal{t}\) skirstinio su 5 laisvės laipsniais, bus mažesnė už 1,3?
7.1.3 Žinome reikšmę, kaip rasti jos įgijimo tikimybę/tikimybės tankį?
Tokio tipo tikimybės gali būti apskaičiuotos tik diskretiesiems dydžiams pagal tikimybės masės funkciją. Jei dydžiai yra tolydieji, konkrečios reikšmės įgijimo tikimybė yra lygi nuliui. Šitokiu atveju galime apskaičiuoti nebent tik tikimybės tankį ties konkrečia reikšme, bet ne jos įgijimo tikimybę.
Užduotis 7.3
- Žinoma, kad \(X \sim \mathcal{P}(2)\). Apskaičiuokite tikimybę \(P(X = 4)\).
7.2 Programos GeoGebra tikimybių skaičiuoklė
Programa „GeoGebra“ yra nemokamas įrankių rinkinys įvairiems matematiniams (geometriniams, statistiniams ir kitiems) skaičiavimams. Programą galima parsisiųsti į savo kompiuterį, planšetę arba naudoti internetinę versiją (www.geogebra.org/classic/probability ). Mums reikalingas įrankis – tikimybių skaičiuoklė, su kuria supažindinama video epizoduose 7.1, 7.2 (sukurti ankstesnių metų kursui), 7.3 (dabartinė versija) bei perskaičius šias instrukcijas:
- „Probability Calculator“ – trumpa instrukcija, kaip naudotis tikimybių skaičiuokle (nuoroda );
Video epizodas 7.1 Programos „GeoGebra“ tikimybių skaičiuoklė: įvadas.
Video epizodas 7.2 Bendrieji principai, kaip spręsti tikimybinius uždavinius programos „GeoGebra“ tikimybių skaičiuokle: konkrečių reikšmių įgijimo tikimybių, tikimybių įgyti reikšmę iš tam tikro intervalo, su tikimybėmis susietų kvantilių, ats.d. vidurkio ir standartinio nuokrypio apskaičiavimas.
Žemiau esančiame epizode viename iš uždavinių yra rašybos klaida. Atsiprašau už netikslumą.
Video epizodas 7.3 „GeoGebra“ tikimybių skaičiuoklė uždaviniams spręsti (su uždavinių pavyzdžiais).
Užduotis 7.4 Išspręskite šiuos uždavinius:
- Žąsų migracija. Daugiamečių stebėjimų duomenimis, žąsų migracija pavasarį užtrunka vidutiniškai 4 dienas (SD = 1,3 dienos). Darykime prielaidą, kad kelionės trukmės skirstinys yra normalusis. Kokia tikimybė, kad šiemet migracija:
- baigsis greičiau nei per 6 dienas?
- užtruks ilgiau nei 6 dienas?
- užtruks ne mažiau kaip 2, bet ne daugiau kaip 5 dienas?
- Koks migracijos trukmės 10% procentilis?
- SD – standartinis nuokrypis.
- Kelionė į paskaitą. Vidutiniškai kelionė į biostatistikos paskaitą užtrunka 40 min \((\sigma = 10~min)\). Sakykime, kad kelionės trukmės skirstinys – normalusis.
- Kokia tikimybė, kad kelionė užtruks daugiau nei 50 min?
- Kokia tikimybė, kad kelionė užtruks mažiau nei 55 min?
- Nurodykite labiausiai tikėtinų kelionės trukmių intervalą (trumpiausią ir ilgiausią trukmę), atmetus 5% trumpiausių ir 5% ilgiausių kelionių.
- Nurodykite labiausiai tikėtinų kelionės trukmių intervalą, apibrėžiantį, kiek laiko įprastai užtrunka kelionė 95% kartų, atmetus vienodą kiekį išskirtinai trumpiausių ir išskirtinai ilgiausių kelionių.
- Kokia tikimybė, kad kelionė užtruks lygiai 30 min?
- Sėklos – 1. Sėjant sėklas vienos sėklos sudygimo tikimybė – 75%.
- Kokia tikimybė, kad pasėjus 50 tokių sėklų sudygs ne daugiau kaip 40 iš jų?
- Įvertinkite, kiek vidutiniškai sėklų reikia pasėti, kad sudygtų 20, ir koks reikiamo pasėti sėklų skaičiaus standartinis nuokrypis.
- Kokia tikimybė, kad pasėjus 20 sėklų sudygs bent 75% iš jų?