11. Hipotezių tikrinimas (HT): įvadas
Kai pagal imtį tiriame visą generalinę aibę (GA), kuri yra mažesnė nei GA, tyrimo metu gauti rezultatai yra su paklaidomis. Tad imtyje stebimi skirtumai gali atsirasti dėl 2 priežasčių:
- dėl to, kad tie skirtumai iš tiesų yra generalinėje aibėje;
- dėl atsitiktinumo ir paklaidų.
Todėl net ir matydami skirtumus imtyje, negalime būti visiškai tikri, ar jie iš tiesų egzistuoja. Norėdami sužinoti, ar turime pagrindo atmesti, jog skirtumai atsirado grynai dėl atsitiktinumo, atliekame formalią statistinių hipotezių tikrinimo procedūrą.
Užsiėmimo tikslas – susipažinti su statistinių hipotezių tikrinimo principais.
11.1 Svarbiausios sąvokos
Šiame poskyryje pateikti supaprastinti svarbiausių sąvokų paaiškinimai. Matematiškai griežtų apibrėžimų ieškokite kituose literatūros šaltiniuose.
Efektu galime pavadinti tam tikrą rezultatą, kurio ieškome (kurį tiriame) atlikdami tyrimą: matematine prasme įprastai tai (vidutinis) skirtumas tarp grupių, nuokrypis (nuo tam tikro skirstinio) ar sąsaja (ryšys) tarp kintamųjų. Pvz., tyrimo metu efektu gali būti laikomas kraujospūdžio pokytis (pats reiškinys), atsirandantis (arba ne) dėl suvartoto preparato.
Efekto dydis (angl. effect size) – kiekybinis ieškomo rezultato (pvz., skirtumo dydžio, nuokrypio dydžio ar ryšio stiprumo) įvertis. Pvz., kraujospūdžio pokytis milimetrais pagal gyvsidabrio stulpelį (mmHg) arba širdies ritmo pokytis santykiniais matavimo vienetais, koreliacijos stiprumas tarp ūgio ir svorio.
Statistinių hipotezių tikrinimas yra procedūra, kurios metu pasirenkame tarp nulinės ir alternatyvios hipotezės.
Statistinės nulinės hipotezės \(H_0\) patvirtinti ar įrodyti neįmanoma. Statistinių hipotezių tikrinimo procedūra tiesiog parodo, ar yra pagrindo atmesti \(H_0\).
Nulinė hipotezė (žymima \(H_0\)). Bendrasis principas – statistinė nulinė hipotezė teigia, kad skirtumas, nuokrypis ar ryšio stiprumas yra lygus nuliui. T.y., kad, pvz., kelių grupių lyginamieji parametrai yra vienodi, skirtumo, nuokrypio ar efekto nėra. Ją formuluojant matematiškai gali būti naudojama lygybė arba negriežtos nelygybės \((=, ~\le, ~\ge)\). Norint pabrėžti, kad skirtumo nėra, įprastai rašoma tik lygybė \((=)\). Nulinės statistinės hipotezės patvirtinti ar įrodyti neįmanoma, bet galima teigti, kad jos atmesti nėra pagrindo. O jei yra pagrindo ją atmesti, tada galime taip ir padaryti bei priimti alternatyviąją hipotezę.
Galima išvesti tokią analogiją: nulinė hipotezė \(H_0\) taip vadinama todėl, kad įprastai teigia, jog skirtumas, nuokrypis ar ryšio stiprumas yra lygus nuliui.
Jei nulinė hipotezė formuluojama kitaip, tai laikantis matematinės logikos ją galima performuluoti taip, kad aiškiai matytųsi lygybė nuliui. Pvz.:
- \(A = -12 ~~~ → ~~~ A + 12 = 0\);
- \(A/B = 1 ~~~ → ~~~ A = B ~~~ → ~~~ A - B = 0\);
- „Ats.d. \(X\) skirstosi pagal normalųjį skirstinį“ \(→\) „Nuokrypis nuo normalumo lygus nuliui“ ar „Skirtumas tarp ats.d. \(X\) skirstinio bei teorinio normaliojo skirstinio lygus nuliui“;
- „Ryšio tarp kintamųjų nėra“ \(→\) „Ryšio stiprumas lygus nuliui“;
- „Koreliacijos tarp kintamųjų nėra“ \(→\) „Koreliacijos stiprumas lygus nuliui“.
Jei neturime objektyvaus pagrindo daryti kitaip, privalome naudoti dvipusę alternatyvą.
Statistinis kriterijus (angl., statistical test) – tai taisyklė, pagal kurią atliekamas statistinių hipotezių tikrinimas.
Kriterijaus statistika (angl. test statistic ) – tai atsitiktinis dydis, skaičiuojamas iš duomenų, naudojamas statistinių hipotezių tikrinimo metu. Pagal tyrimo metu gautą kriterijaus statistikos reikšmę skaičiuojama \(p\) reikšmė.
\(p\) reikšmė (angl. \(p\) value ) – tai tikimybė vien tik dėl atsitiktinumo iš imties duomenų gauti bent tiek nuo nuline hipoteze apibrėžto rezultato nukrypusią kriterijaus statistikos reikšmę, kiek tyrimo metu gautoji, jei iš tiesų generalinėje aibėje to skirtumo nebūtų, t.y., jei nulinė hipotezė būtų teisinga (t.p. žiūrėti skyriuje „11.5 Kaip „veikia“ statistiniai kriterijai?“).
\(p\) reikšmė nėra tikimybė, kad \(H_0\) yra teisinga.
\(p\) reikšmė parodo, kaip labai tikėtina gauti tokį rezultatą (pvz., ne mažesnį skirtumą nei gautasis), jei \(H_0\) yra teisinga (neformalus paaiškinimas).
Reikšmingumo lygmuo \(\alpha\). Apskaičiuotąsias \(p\) reikšmes lyginame su reikšmingumo lygmeniu, žymimu \(\alpha\), kuris moksle įprastai lygus \(0{,}05\), t.y., 1/20 (medicinoje gali būti 0,01, inžinerijoje – 0,10). Tai subjektyviai pasirinkta sutartinė reikšmė. Jei neturite pagrindo daryti kitaip, jūs turėtumėte rinktis šį skaičių (0,05).
Išvadų formulavimas. Jei \(p\) reikšmė didelė \((p \ge \alpha)\), tada teigiame, kad skirtumas, nuokrypis, ryšys ar kitoks efektas yra statistiškai nereikšmingas (pastaba: nekorektiška teigti, kad skirtumo, nuokrypio, ryšio ar kitokio efekto nėra: jis yra imtyje, tik laikome, kad statistiškai nereikšmingas, t.y., neturime pagrindo teigti, kad jis yra ir GA). Kai \(p\) reikšmė yra maža \((p<\alpha)\), tada teigiame, kad tokį skirtumą, nuokrypį ar ryšio stiprumą gauti vien dėl atsitiktinumo yra mažai tikėtina, ir sakome, kad rezultatas yra statistiškai reikšmingas.
Taip pat turėtume prisiminti, kad, griežčiau kalbant, tikrinant statistines hipotezes, klausimą reikėtų formuluot taip: „Ar, sprendžiant iš turimų duomenų, pakanka pagrindo teigti, kad efektas (skirtumas/nuokrypis/ryšys) yra ir GA?“. Tada atlikta analizė gali pateikti atsakymą, arba „Taip, pakanka pagrindo taip teigti: vien tik imties atsitiktinumu jį paaiškinti būtų sunku“ (t.y., efektas yra statistiškai reikšmingas), arba „Ne, nepakanka pagrindo taip teigti: jį galima paaiškinti vien tik imties atsitiktinumu“ (t.y., efektas yra statistiškai nereikšmingas). Bet tai, kad neužtenka pagrindo taip teigti, nereiškia, kad to nėra.
Tam tikra prasme „statistiškai nereikšmingas“ reiškia „paklaida yra per didelė, jog galėtume teigti, kad efektas yra“, o „statistiškai reikšmingas“ reiškia „paklaida yra pakankamai maža“.
Galimi du tikrovės variantai: skirtumas GA iš tiesų yra arba jo iš tiesų nėra. Darydami tam tikrą išvadą mes galime būti teisūs, bet galime ir apsirikti.
Pirmos rūšies klaida – klaidingai atrasti tai, ko nėra (pvz., diagnozė „nėščias vyras“ – klaidingai nustatytas nėštumas): teigti, kad skirtumas yra, kai iš tiesų jo nėra (t.y., kai nulinė hipotezė yra teisinga). Pirmos rūšies klaidos tikimybę žymėsime \(\alpha\) (tai tas pats reikšmingumo lygmuo).
Antros rūšies klaida – klaidingai nepastebėti, „pražiopsoti“ (pvz., nėščiai moteriai diagnozuoti, kad ji nesilaukia): teigti, kad skirtumo nėra, kai iš tiesų jis yra (t.y., kai alternatyvioji hipotezė yra teisinga). Antros rūšies klaidos tikimybę žymėsime \(\beta.\)
Kriterijaus galia \((1-\beta)\) – tai tikimybė atmesti antros rūšies klaidą ir teisingai atrasti skirtumą ar ryšį, kuris egzistuoja. Toje pačioje situacijoje, kuo labiau padidiname skaitinę reikšmingumo lygmens \(\alpha\) reikšmę, pvz., nuo 0,01 iki 0,05 (didėja tikimybė padaryti I rūšies klaidą), tuo kriterijaus galia tampa didesnė (mažėja tikimybė padaryti II rūšies klaidą).
Sakykime, kad efektas iš tiesų egzistuoja. Kas lemia padidėjusią klaidų tikimybę? Tikrindami stat. hipotezes, mes fiksuojame I rūšies klaidos tikimybę iš anksto pasirinkdami reikšmingumo lygmenį \(\alpha\). Tad kinta tik II rūšies klaidos tikimybė. Jos dydis priklauso nuo imties dydžio, duomenų sklaidos dydžio, efekto dydžio ir naudojamo statistinio kriterijaus.
- Hipotezių tikrinimas ir imties dydis:
- Kuo imtis mažesnė, tuo \(H_0\) atmetama rečiau. Dažna priežastis – per maža kriterijaus galia. Kuo mažesnė imtis, tuo daugiau vietos atsitiktinumui.
- Kuo imtis didesnė, tuo \(H_0\) atmetama dažniau. Priežastis – didėjant imčiai ir esant tam pačiam reikšmingumo lygmeniui kriterijaus galia auga. Kuo didesnė imtis, tuo labiau pasitikime tyrimo metu gautu rezultatu, nes mažėja paklaidos. Deja, labai didelėms imtims statistiškai reikšmingais gali būti pripažįstami net labai maži skirtumai (maži efektai).
- Hipotezių tikrinimas ir duomenų reikšmių sklaida:
- Kuo didesnė sklaida, tuo didesnis neapibrėžtumas. Tad jei visi kiti parametrai nekinta, tai kuo sklaida mažesnė, tuo lengviau pasiekti statistinį reikšmingumą.
- Įprastai įtakos sklaidai tyrėjas daryti negali, nes tai duomenų savybė. Tad kuo didesnė sklaida, tuo didesnio imties dydžio reikia norint pasiekti statistinį reikšmingumą.
- Hipotezių tikrinimas ir efekto dydis.
- Efekto dydis yra duomenų savybė, tad tyrėjas jo dydžio keisti negali (tačiau nori kuo tiksliau nustatyti).
- Kuo efekto dydis didesnis (t.y., kuo ryškesni skirtumai), tuo mažesnio imties dydžio reikia norint pasiekti statistinį reikšmingumą. Tad, pvz., jei tikroji koreliacijos koeficiento reikšmė \(\varrho = 0{,}82\), tai norint pasiekti statistinį reikšmingumą (gauti pakankamai mažą paklaidą) reikės mažesnio imties dydžio nei tuo atveju, kai \(\varrho = 0{,}09\).
- Hipotezių tikrinimas ir pasirinktas stat. kriterijus.
- Tai pačiai situacijai gali tikti keli kriterijai. Tad geriau rinktis tą, kuris pasižymi didesne kriterijaus galia. Pvz., jei reikia rinktis tarp parametrinio ir neparametrinio kriterijų ir abiems keliamos sąlygos yra tenkinamos, tai geriau rinktis parametrinį, nes jo kriterijaus galia didesnė. Visgi, jei parametrinės sąlygos netenkinamos, parametrinio kriterijaus reiktų nesirinkti.
Statistinis reikšmingumas netapatus praktinei naudai (praktiniam reikšmingumui). Statistinis reikšmingumas parodo, ar labai tikėtina gauti ne mažesnį skirtumą iš imties duomenų nei gautasis, jei iš tiesų GA skirtumo nėra, bet nieko nesako apie tai, kokio dydžio tas skirtumas. Dėl šios priežasties be statistinio reikšmingumo būtina įvertinti ir efekto dydį (standartizuota ar nestandartizuota išraiška).
Pirmos ir antros rūšies klaidų tikimybės, imties dydis ir efekto dydis yra susiję: jei turime tinkamą statistinį modelį, žinant ar numanant trijų čia išvardintų dydžių reikšmes, ketvirtojo reikšmę dažniausiai galime apsiskaičiuoti. Įprastai tas ketvirtasis, kurio reikšmės nežinome, būna arba imties dydis, arba antros rūšies klaidos tikimybė. Analizė, kurios metu įvertiname kriterijaus galią arba reikiamą imties dydį, kad būtų pasiekta norimo dydžio kriterijaus galia, dažnai vadinama (statistinės) galios analize. Pastaba, tokios analizės metu įprastai modeliuojama, kokio imties dydžio reikia norint pasiekti 80% kriterijaus galią.
Detalesnio ir matematiškai griežtesnio daugelio iš šiame skyriuje pateiktų sąvokų paaiškinimo galite ieškoti vadovėlyje (Čekanavičius ir Murauskas 2006, p.137–148) arba kituose šaltiniuose.
11.2 Analizės, į kurią įtrauktas statistinių hipotezių tikrinimas, eiga
Statistinių hipotezių tikrinimas yra patvirtinančiosios (angl. confirmatory) analizės tipas. Hipotezių tikrinimą atliekame tam, kad patikrintume iš anksto išsikeltą hipotezę, o ne tam, kad keltume naujas idėjas. (Kelti naujas idėjas – tai žvalgomosios analizės tikslas).
Tyrimo, į kurį įtrauktas ir statistinių hipotezių tikrinimas, eigą reiktų suskirstyti 2 pagrindinius etapus:
- Dalykai, kurie privalo būti pasirinkti ar padaryti prieš pamatant duomenis;
- Dalykai, kuriuos galima daryti ar patikslinti, kai duomenys jau įkelti į analizės programą.
Vienas iš tyrimo eigos variantų (konkrečiu atveju gali būti daugiau variacijų):
- Apsibrėžiame duomenų analizės klausimą.
- Formuluojame biologinę (ar kitos specialybinės srities) nulinę ir alternatyviąją hipotezę.
- Formuluojame statistinę nulinę ir alternatyviąją hipotezę.
- Pasirenkame analizės metodą: pagal kintamųjų kiekį, duomenų tipus, išsikeltas hipotezes ir kitus šiuo metu žinomus aspektus pasirenkame statistinį kriterijų.
- Pasirenkame analizės parametrus, tokius kaip:
- reikšmingumo lygmuo \((\alpha)\). Moksle priimta naudoti \(\alpha = 0{,}05\) (nors iš tiesų tai subjektyvus pasirinkimas), tad jei neturime objektyvaus pagrindo daryti kitaip, renkamės 0,05.
- alternatyvos tipas \((\ne, ~<, ~>)\). Jei neturime objektyvaus pagrindimo daryti kitaip, renkamės dvipusę alternatyvą \((\ne)\).
- Jei lyginamos kelios grupės, kokią grupių lyginimo strategiją naudosite (kiekvienas su kiekvienu, kiekvienas su kontrole ar pan.)
- Jei hipotezes tikrinsime kelis kartus (pvz., jei lyginsite kelias grupes tarpusavyje), kokią I rūšies klaidos padidėjimo prevencijos procedūrą naudosime (Benjamini-Hochberg, Holm, Bonferroni ar pan.)
- Jei įmanoma, atliekame galios analizę ir preliminariai įvertiname, koks imties dydis būtų tinkamas.
- Tinkamai suplanuojame kitus tyrimo aspektus.
- Korektiškai atliekame tyrimą ir surenkame duomenis, skirtus patikrinti hipotezę.
Tik po to, kai iškelta (ir užrašyta) hipotezė (nulinė ir alternatyvioji) ir pasirenkami parametrai, turėtų būti renkami ir analizuojami duomenys, skirti ją patikrinti. „Pažiūrėjus“ į duomenis, hipotezės ir parametrų keisti nebegalima.
- Atliekame išsamią aprašomąją statistiką (tokią, kuri padeda susipažinti su duomenimis, pastebėti neatitikimus ir tendencijas bei atsakyti į tyrimo klausimą): braižome reikiamus grafikus (svarbu!), skaičiuojame aprašomąsias statistikas, sudarome lenteles. Atsižvelgę į jas – pradedame vertinti, ar tenkinamos analizės prielaidos.
Labai svarbu nusibraižyti tinkamą grafiką.
- Patikriname pasirinktos analizės prielaidas ir kitus reikalavimus. Jei jie netenkinami, parenkame kitą – tinkamesnį – analizės metodą.
- Pagal klausimą ir duomenų savybes (kintamųjų tipą, kintamųjų skaičių, imties dydį, normalumo, lygių dispersijų ir kitas prielaidas, kurias turi tenkinti duomenys) pasirenkamas tik vienas labiausiai tinkantis analizės metodas.
- Taikomas pasirinktas hipotezių tikrinimo metodas. Tarp kitų rezultatų, gaunama ir \(p\) reikšmė, pagal kurią darome išvadą apie rezultato (ne duomenų6) statistinį reikšmingumą (ar nereikšmingumą).
Statistinis reikšmingumas yra analizės rezultato (statistinio efekto), o ne
duomenųsavybė. - Įvertiname (standartizuotą arba/ir nestandartizuotą) efekto dydį – pagal jį spendžiame apie praktinę naudą. Įprastai norime, kad efektas būtų kuo didesnis, tad geriausia, jei iš literatūros ar kitų šaltinių žinome, kokia mažiausia efekto dydžio vertė rodo pakankamai didelę naudą (pvz., ar temperatūros pokytis 0,01 laipsnio dalimi mūsų tyrime yra praktiškai naudingas?). Tačiau norint daryti pagrįstas išvadas, pirmiausia efektas turi būti statistiškai reikšmingas.
- Pagal visos analizės (aprašomąją statistiką, hipotezių tikrinimą, efekto dydį ir kt.) rezultatus darome galutinę tyrimo išvadą.
- Analizės rezultatus tinkamai aprašome.
Rekomenduoju peržvelgti (McDonald 2014l) patarimus, kaip atlikti biologinių duomenų analizę („Step-by-step analysis of biological data“ ). Apie parametrinių statistinių hipotezių taikymo etapus rašo (Čekanavičius ir Murauskas 2006, p.142–144): šiame šaltinyje ypač vertinga dalis apie išvadų formulavimą.
11.3 Prielaidos ir reikalavimai
Jau pastebėjote, kad tikrinant hipotezes yra skaičiuojamos tikimybės. Realioms gyvenimiškoms situacijoms tikimybes apskaičiuoti tiksliai yra sudėtingas uždavinys. Todėl sudarant įvairius statistinius kriterijus daromos tam tikros prielaidos, kurias tenkinant tikimybės apskaičiuojamos pakankamai tiksliai. Jei prielaidos pažeidžiamos, kriterijų naudoti nekorektiška. Todėl turite pasirinkti tą kriterijų, kuris tinka būtent jūsų duomenims.
Dažnai daromos tokios prielaidos, kai analizuojami kiekybiniai duomenys:
- duomenys yra reprezentatyvūs generalinei aibei (tyrimas atliktas ir duomenys surinkti korektiškai, imtis tikimybinė, o duomenų kiekvienoje grupėje pakankamai daug);
- tiriamieji yra tarpusavyje nepriklausomi (nemaišyti su nepriklausomomis ir kartotinėmis imtimis);
- kiekvienos grupės pasiskirstymas yra normalusis;
- grupių dispersijos yra lygios.
Taip pat pagal tai, kaip suplanavome eksperimentą, duomenų imtys (grupės) būna arba nepriklausomos, arba kartotinės, arba mišraus tipo7. Toliau nustatome ir kiek tų grupių turime analizės metu, kokie grupių dydžiai. Kartais svarbu ir tai, ar grupės vienodo dydžio. Nuo šių savybių priklauso, kokius analizės metodus rinksimės.
11.4 Parametriniai ir neparametriniai kriterijai
Statistiniai kriterijai (angl. statistical tests) skirstomi į parametrinius ir neparametrinius. Jei kriterijus išvestas grindžiant prielaida, kad tiriami duomenys yra pasiskirstę pagal tam tikrą žinomą teorinį skirstinį (pvz., normalųjį) – toks kriterijus vadinamas parametriniu. Tad norint gauti korektišką rezultatą, duomenys turėtų tenkinti šią prielaidą. Ir jei:
- duomenų pasiskirstymas bent vienoje imtyje/grupėje nėra normalusis:
- kai imtys labai didelės, tada kai kuriems kriterijams gali būti taikomos išlygos,
- duomenys yra ranginiai,
- duomenų imtys/grupės labai mažos (tarkime, \(n_i < 20\), kur \(n_i\) yra i-tosios grupės dydis),
- duomenyse yra aiškių išskirčių,
tada naudojami neparametriniai (nuo skirstinio formos nepriklausomi) kriterijai.
Dažnai neparametrinių kriterijų statistinė galia yra mažesnė, tad jei galite rinktis, naudokite parametrinį kriterijų.
Verta žinoti, kad taikant tiek parametrinius, tiek ir neparametrinius kriterijus, duomenys privalo tenkinti tam tikras sąlygas (reiktų atidžiai perskaityti naudojamo kriterijaus aprašymą).
Jei tai pačiai situacijai tinka ir parametrinis, ir neparametrinis kriterijus, rinkitės parametrinį (jo kriterijaus galia įprastai yra didesnė).
Jei pažeidžiamos parametriniam kriterijui keliamos sąlygos, geriau rinktis neparametrinį.
Kiekybiniams duomenims taikant:
- parametrinį metodą, kartu įprasta nurodyti vidurkį ir standartinį nuokrypį,
- o taikant neparametrinį – medianą ir, sakykim, kvartilius.
Detalesnį įvadą į neparametrinius metodus galite rasti (Čekanavičius ir Murauskas 2004, p.7–12).
11.5 Kaip „veikia“ statistiniai kriterijai?
Sakykime, kad tyrimo problemą ir hipotezę suformulavome. Paanalizuokime, kaip „veikia“ statistinis kriterijus.
- Statistinio kriterijaus statistikos parinkimas. Atliekant analizę, įprastai norima iš imties duomenų įvertinti skirtumą, nuokrypį arba ryšio stiprumą (t.y., efektą) generalinėje aibėje. Sudarant imtis visada egzistuoja atsitiktinumas, tad skaičiuojant rezultatus atsiranda paklaidos. Siekiant atlikti statistinės hipotezės vertinimą, pagal analizuojamą problemą ir duomenų savybes parenkamas toks skirtumo, nuokrypio ar ryšio stiprumo vertinimo matas (jis ir vadinamas kriterijaus statistika), kurio skirstinys gali būti apskaičiuotas situacijai, kai generalinėje aibėje skirtumo, nuokrypio ar ryšio nėra (t.y., jei nulinė hipotezė \(H_0\) būtų teisinga).
- Sudaromas kriterijaus statistikos skirstinys, kai \(H_0\) teisinga. Naudojantis statistikos teorija ir duomenimis, sudaromas kriterijaus statistikos skirstinys situacijai, kai \(H_0\) yra teisinga.
- Apskaičiuojama kriterijaus statistikos reikšmė. Iš duomenų apskaičiuojama viena konkreti kriterijaus statistikos reikšmė (empirinė reikšmė), kuri bus panaudota tolimesniuose skaičiavimuose.
- Skaičiuojama \(p\) reikšmė. Pagal sudarytą skirstinį ir gautą empirinę kriterijaus statistikos reikšmę skaičiuojama tikimybė gauti nemažiau nuo taško, rodančio, kad skirtumo, nuokrypio ar ryšio nėra, nutolusią kriterijaus statistikos reikšmę, jei nulinė hipotezė yra teisinga. Atkreipkite dėmesį, kad skirtingų alternatyvų atveju \((\ne, ~ <, ~ >)\) tikimybė skaičiuojama skirtingai.
- Priimama statistinė išvada. Gautoji \(p\) reikšmė lyginama su iš anksto pasirinktu reikšmingumo lygmeniu \(\alpha\):
- kai \(p < \alpha\), sakome, kad rezultatas yra statistiškai reikšmingas (galime generalizuoti visai generalinei aibei, GA);
- kai \(p \ge \alpha\), sakome, kad rezultatas yra statistiškai nereikšmingas (didelė tikimybė tokį rezultatą gauti grynai dėl imties atsitiktinumo, tad negalime generalizuoti visai GA). Įprastai toks rezultatas rodo, arba kad imtis per maža norint teigti, kad tiriamasis efektas yra statistiškai reikšmingas, arba kad to tiriamojo efekto nėra.
Panagrinėkime konkretų pavyzdį.
11.5.1 Apie t kriterijaus taikymą ir p reikšmių skaičiavimą
Šiame skyriuje vienos imties \(t\) kriterijaus pavyzdžiu iliustruosime, kaip „veikia“ statistiniai kriterijai.
Vienos imties \(t\) kriterijus naudojamas norint patikrinti hipotezę apie vidurkio ir tam tikros konkrečios reikšmės (pavadinkime ją konstanta) skirtumą. Analizei tinka normaliai pasiskirstę duomenys (parametrinis kriterijus).
Apskaičiuojama kriterijaus statistika. Statistika \(t\) skaičiuojama pagal tokią formulę: \[\begin{equation} t = \frac{\overline{x} - a}{s_x/\sqrt{n}} \tag{11.1} \end{equation}\]Čia \(a\) – skaičius, su kuriuo lyginame, \(\overline{x}\) – vidurkis, \((s_x/\sqrt{n})\) – standartinė vidurkio paklaida, \(s_x\) – standartinis nuokrypis, \(n\) – imties dydis. Kaip matote, skaitiklyje yra apibrėžiamas skirtumas, o vardikliu jis yra normuojamas.
Sudaromas statistikos skirstinys, kai \(H_0\) teisinga. Klasikinio Stjudento \(t\) kriterijaus atveju, \(t\) statistika (kai \(H_0\) teisinga) yra pasiskirsčiusi pagal Stjudento skirstinį su \(n - 1\) laisvės laipsnių. Atkreipkite dėmesį, kad šio skirstinio centras yra ties skaičiumi 0 (ten, kur skirtumo nėra). Šį skirstinį galite nusibraižyti programos „GeoGebra“ tikimybių skaičiuokle .
Skaičiuojama \(p\) reikšmė. Pagal apskaičiuotą \(t\) reikšmę ir jai parinktą skirstinį apskaičiuojame \(p\) reikšmę. Skaičiavimas priklauso nuo pasirinktos alternatyvos. Skaičiavimo principai atitinkamai vienpusės „daugiau už“, vienpusės „mažiau už“ ir dvipusės „nelygu“ alternatyvos atveju pateikti paveiksluose 11.1, 11.2 ir 11.3.

Pav. 11.1: Sąsaja tarp programos „R“ rezultatų ir \(p\) reikšmių skaičiavimo programos „GeoGebra“ tikimybių skaičiuokle vienpusės alternatyviosios hipotezės „daugiau už“ atveju.
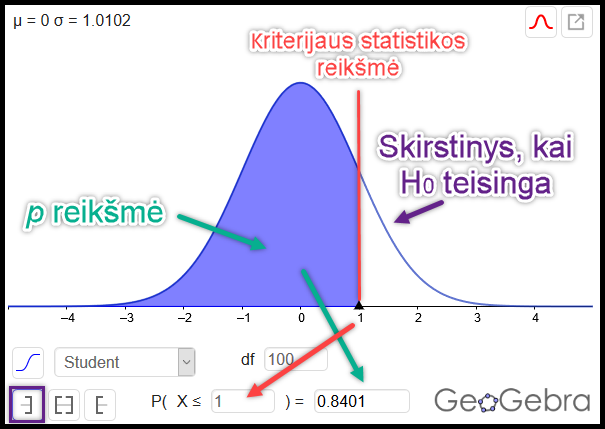
Pav. 11.2: \(P\) reikšmių skaičiavimas programos „GeoGebra“ tikimybių skaičiuokle vienpusės alternatyviosios hipotezės „mažiau už“ atveju.
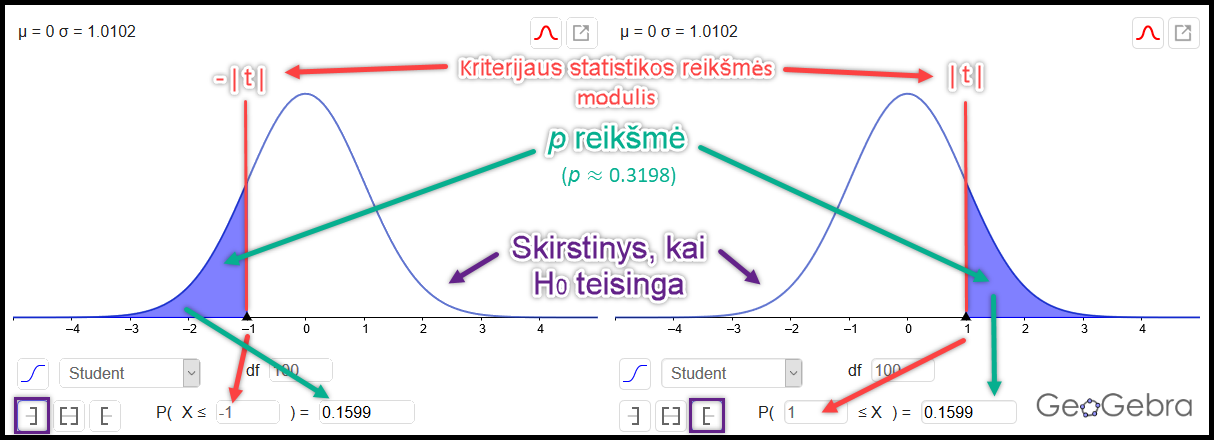
Pav. 11.3: \(P\) reikšmių skaičiavimas programos „GeoGebra“ tikimybių skaičiuokle dvipusės alternatyviosios hipotezės („nelygu“) atveju. Gautasis rezultatas iš tiesų yra tikimybių „mažiau už“ ir „daugiau už“ suma. Pavyzdyje naudojamas Stjudento \(t\) skirstinys: jis yra simetriškas nulio atžvilgiu. Atkreipkite dėmesį į tai, kad skaičiavimuose naudojama absoliučioji kriterijaus statistikos reikšmė (
|t|).Priimama statistinė išvada. Lyginame \(p\) su \(\alpha\). Matome, kad nuo alternatyvos tipo priklauso \(p\) reikšmės dydis ir, galimai, statistinė išvada. Dėl to, siekiant visiškai korektiško ir nešališko rezultato, svarbu, kad alternatyvą bei reikšmingumo lygmenį apsibrėžtumėte prieš pamatydami duomenis.
11.6 Kriterijai 1, 2 ir kelioms imtims
Kuo skiriasi statistiniai kriterijai 1-2 imtims ir kriterijai daugiau nei 2 imtims?
Vienos ar dviejų imčių kriterijai tik labai retais atvejais neturi vienpusių alternatyvų, tad turi ir vienpuses, ir dvipuses. T.y., tinka tokiems klausimams, kur reikia patikrinti, ar, pvz., viena grupė pagal tam tikrą požymį yra ne mažesnė už kitą.
Kelių (2 ir daugiau) imčių (grupių) kriterijai įprastai turi tik dvipuses alternatyvas, o pats kriterijus rodo, ar bent dvi grupės skiriasi tarpusavyje, bet nerodo, kurios tiksliai. Tad jei tokios analizės metu gauname reikšmingą rezultatą \(p < \alpha\), analizę tęsiame toliau norėdami išsiaiškinti, kurios grupių poros skiriasi tarpusavyje (jei lyginame kiekvieną su kiekviena) arba kurios grupės skiriasi nuo kontrolės (jei lyginame tik su kontrole). Tokia analizė po pagrindinio kriterijaus taikymo (gavus statistiškai reikšmingus rezultatus) vadinama post-hoc analize (skaitoma „post-hok“).
Post-hoc analizė atliekama tik tada, jei pagrindinės analizės rezultatas yra statistiškai reikšmingas.
11.7 Rezultatų aprašymo principai
Kai aprašote analizės rezultatus, pirmiausia laikykitės tų reikalavimų, kuriuos nurodo tie subjektai, kuriems atliekate analizę (pvz., laikykitės žurnalo, kursinio darbo ar darbo grupės reikalavimų). Jei subjektai reikalavimų nepateikia, tada laikykitės šių gairių:
- Žmogus, turintis pakankamai žinių, pagal jūsų pateiktą aprašymą turėtų galėti atkartoti jūsų analizę ir nagrinėdamas rezultatus turėtų tiksliai suprasti, kaip jie buvo gauti.
- Išsamiame statistinių rezultatų aprašyme turi matytis, kas buvo analizuota, pateikta išvada („statistiškai reikšmingas/nereikšmingas“) ir jos pagrindimas: tikslus kriterijaus (testo, metodo) pavadinimas, alternatyva (vienpusė ar dvipusė), kriterijaus statistika (\(t, F, \chi^2\) ar kita), parametrai (įprastai 2 skaitmenų po kablelio tikslumu arba sveikieji skaičiai) ir, būtinai, \(p\) reikšmė (įprastai 3 skaitmenų po kablelio tikslumu), imties dydis (jei nenurodytas kitur). Taip pat rekomenduojama pateikti efekto dydį (standartizuotą arba pradiniais vienetais) ir jo pasikliautinąjį intervalą. Pavyzdys pateiktas pav. 11.4. Daugiau pavyzdžių galite rasti šioje svetainėje (Kahn 2010).
{target="_blank"}.](fig/pic/08/stats_reporting_format.png)
Pav. 11.4: Rekomenduojamas statistinio metodo rezultatų pateikimo formatas. Šaltinis: indrajeetpatil.github.io/statsExpressions.
- Rekomenduoju \(p\) reikšmes rašyti 3 (arba 4) skaitmenų po kablelio tikslumu. Jei \(p\) labai maža, rašykite, pvz., \(p<0{,}001\), jei labai didelė – \(p>0{,}999\) (jei apvalinate daugiau nei 3 skaitmenų po kablelio tikslumu, šiuos skaičius atitinkamai pakeiskite).
- Turi būti paaiškinti visi trumpiniai. Pvz., kad „95% PI“ yra 95% pasikliautinasis intervalas.
- Visos to paties atsitiktinio dydžio statistikos (vidurkiai, medianos, standartiniai nuokrypiai, kvantiliai, pasikliautinieji intervalai, …), kurie matuojami tais pačiais matavimo vienetais, privalo būti suapvalinti tuo pačiu tikslumu.
- Iš aprašymo turi matytis, koks yra efekto dydis. Pvz., jei lyginama skirstinių padėtis ir taikomi parametriniai kriterijai (lyginami vidurkiai) – tada turi būti pateikti kiekvienos grupės vidurkiai. Taip pat gali būti pateiktas vidurkių skirtumas ir jo pasikliautinasis intervalas. Jei tam pačiam uždaviniui taikomi neparametriniai metodai – aprašyme pateikiamos medianos. Jei lyginamos dispersijos – turi būti pateiktos dispersijos. Jei lyginamos proporcijos – pateikiamos proporcijos. Jei grupių daug, rezultatai gali būti pateikti lentele pateikiant nuorodą tekste. Taip pat siūloma pateikti standartizuotuosius efekto dydžio matus (\(d\), \(g\), \(r\), \(V\), \(r^2\), \(\eta^2\), \(\omega^2\) ar pan., žr. skyriuose 18.3, 19.4, 20, 15.4).
- Taip pat pateikiamas grupių palyginimo grafikas (grupių histogramos, stačiakampės, branduolinio tankio, sklaidos, mozaikinės ar kitos tinkamos diagramos).
- Dažnai reikalaujama, kad aprašyme (pagrindiniame tekste), lentelėje ir grafiškai pateikta informacija nesidubliuotų (skirtingi pateikimo būdai turi vienas kitą papildyti, o ne dubliuoti).
- Metodų dalyje tiksliai aprašomas naudotas metodas. Jei metodas nėra standartinis ar plačiai žinomas, reiktų cituoti šaltinį, kuriame metodas yra aprašytas. Taip pat nurodoma programa, kuria atlikti skaičiavimai, jos versija. Jei dirbant „R“ (ar kita programa) naudotas papildomai atsisiųstas paketas, nurodoma, iš kokio paketo paimta analizės funkcija. Taip pat nurodykite tikslią paketo versiją, nes kitaip rezultatai gali būti neatkartojami.
Daugiau patarimų, kaip teisingai aprašyti dažniausiai pasitaikančias biomedicininių duomenų analizes, rasite (Lang ir Altman 2015) straipsnyje (rekomenduoju; norėdami pasiekti straipsnį, junkitės per VU VPN).
Informacijos šaltiniai
Statistinis reikšmingumas yra analizės rezultato (statistinio efekto), o ne
duomenųsavybė. Duomenys gali būti reprezentatyvūs arba nereprezentatyvūs, patikimi arba nepatikimi (priklausomai nuo to, kaip duomenis rinkote ir koks imties dydis), o rezultatai statistiškai reikšmingi arba ne.↩︎Mūsų kurse mišrių grupių neturėsime↩︎