21. Tiesinė regresija

21.1 Regresinė analizė

Koreliacinė analizė parodo, ar dviejų kintamųjų reikšmės yra susijusios ir koks tos sąsajos stiprumas. Jei šito užtenka, šioje vietoje analizę ir baigiame. Jei norime griežčiau apsirašyti šią sąsają, galime atlikti regresinę analizę.

Regresijos modelis – statistinis modelis, leidžiantis vieno kintamojo reikšmes prognozuoti pagal kito kintamojo reikšmes. Regresija – statistinė vieno atsitiktinio dydžio reikšmių priklausomybė nuo kito – neatsitiktinio – dydžio (arba kelių kitų dydžių), turinti griežtą funkcinį ryšį (t.y., aprašoma lygtimi). Pavyzdžiai:

1. pirmas pavyzdys, kuris ateina į galvą – yra kalibravimas, kai paruošiame žinomos koncentracijos tirpalus, supilstome į kiuvetes bei išmatuojame šviesos sugertį. Susidarome koncentracijos ir šviesos sugerties priklausomybės (t.y., kalibracinę) kreivę bei lygtį. Vėliau į mėgintuvėlį įpylę nežinomos koncentracijos tirpalą pagal šviesos sugerties intensyvumą galime nustatyti koncentraciją. Tai dažnas uždavinys per biochemijos laboratorinius darbus;
2. regresija gali būti naudojama ir tada, kai, tarkime, norime nustatyti, koks įprastai būna pulsas padarius tam tikrą kiekį pritūpimų;
3. koks būna vabzdžio šarvo storis, jei žinome vabzdžio svorį ir ilgį;
4. kaip svoris priklauso nuo amžiaus;
5. kaip plaučių tūris priklauso nuo per savaitę surūkomų cigarečių skaičiaus.

Pagal nepriklausomų kintamųjų \((X)\) skaičių, regresijos modeliai skirstomi į paprastąją (vienas \(X\)) ir daugialypę (keli \(X\)’ai) regresiją.

Paprastosios tiesinės regresijos modelis užrašomas lygtimi: \[Y = a + bX + \varepsilon\] Čia:

• \(Y\) ir \(X\) – mūsų tiriami kintamieji:
  • \(Y\) – vadinamas priklausomu, arba atsako, kintamuoju, nes jį modeliuojame;
  • \(X\) – nepriklausomu, arba aiškinamuoju, kintamuoju, arba regresoriumi, nes pagal jį modeliuojame \(Y\) reikšmes. Daroma prielaida, kad \(X\) yra matuojamas be paklaidų (t.y., nėra atsitiktinis dydis);
• \(a\) ir \(b\) – lygties koeficientai:
  • \(a\) – laisvasis narys, kartais vadinamas konstanta (angl. intercept). Paprastosios regresijos atveju parodo, kurioje vietoje regresijos tiesė kerta y ašį, kai \(X = 0\);
  • \(b\) – koeficientai, dar vadinami krypties koeficientais (angl. slope) arba svertiniais koeficientais. Parodo, kiek pakinta Y reikšmė, kai X reikšmė pakinta vienu vienetu.
  • Atliekant regresinę analizę mūsų tikslas apskaičiuoti šiuos koeficientus.
• \(\varepsilon\) – liekamosios paklaidos, dar vadinamos likučiais (angl. residuals):
  • tai visa kita, nuo ko gali priklausyti Y reikšmės;
  • šios paklaidos – tai kintamojo \(Y\) matavimo paklaidos (nes modelyje laikoma, kad \(X\) matuojamas be paklaidų);
  • pagal paklaidas galime patikrinti daugelį tiesinės regresijos modelio prielaidų.

Daugialypės tiesinės regresijos modelis panašus, tik yra daugiau nepriklausomų kintamųjų ir \(b\) koeficientų. Pvz., kai yra 3 aiškinamieji kintamieji:

\[Y = a + b_1X_1 + b_2X_2 + b_3X_3 + \varepsilon\]

Bendruoju atveju:

\[Y = a + \left( \sum b_iX_i \right)+ \varepsilon\]

21.2 Regresinės analizės eiga

Visą regresinę analizę galima suskirstyti į 3 pagrindinius etapus:

1. Pirmiausia modelis yra sudaromas (parenkami kintamieji, užrašoma regresijos lygtis, apskaičiuojami koeficientai).
2. Tada vykdoma modelio diagnostika (patikrinamas modelio tinkamumas duomenims, duomenų tinkamumas modeliui, modelio prielaidos):
   • jei reikia – modelis tobulinamas.
3. Galiausiai tinkamai sudarytas modelis aprašomas ir naudojamas prognozuoti:
   • ateityje žinodami visų X’ų reikšmes, galėsime prognozuoti, kokia bus tikėtina kintamojo Y reikšmė.

21.3 Tinkamo tiesinės regresijos modelio rodikliai

Tinkamo tiesinės regresijos modelio, pagal kurį galima daryti pagrįstas išvadas, rodikliai (labai išsami regresinė analizė):

1. Determinacijos koeficientas \(R^2 \ge 0{,}20\):
   • kuo \(R^2\) didesnis, tuo glaudžiau taškai išsidėsto apie regresijos tiesę;
   • naudojame tik vieną determinacijos koeficientą, kuris labiau tinka:
     • arba įprastinį: tinka paprastajai tiesinei regresijai arba daugialypei, kai duomenų pakankamai daug – pvz., vienam nepriklausomam kintamajam \(X_i\) tenka bent 7 duomenų taškai;
     • arba koreguotąjį: kai modelyje yra daug nepriklausomų kintamųjų \(X_i\) (ir palyginus mažai taškų), įprastinis \(R^2\) gali būti nepagrįstai didelis.
2. ANOVA \(p < 0{,}05\):
   • parodo, kad bent vienas regresorius yra reikalingas, t.y., bent vieno koeficiento vertė statistiškai reikšmingai skiriasi nuo nulio;
3. Visiems regresoriams t kriterijų \(p < 0{,}05\):
   • parodo, kurių konkrečiai koeficientų vertė statistiškai reikšmingai skiriasi nuo 0;
4. Nėra išskirčių, jei:
   • Bonferroni išskirčių kriterijaus koreguotoji \(p \ge 0{,}05\) (arba NA);
   • Kuko matas d (Cook‘s distance) visiems stebėjimams \(d < 1\).
5. Liekamosios paklaidos normalios:
   • Sprendžiant pagal q-q grafiką bei
   • Shapiro-Wilk testo \(p \ge 0{,}05\).
6. Liekamųjų paklaidų vidurkis lygus 0:
   • Sprendžiant iš liekamųjų paklaidų pagal prognozuojamas reikšmes grafiko bei
   • Vienos imties t testo \(p \ge 0{,}05\).
7. Nėra heteroskedastiškumo problemos:
   • Sprendžiant iš liekamųjų paklaidų grafikų bei
   • Breusch-Pagan (Breušo-Pagano; Briušo-Peigano) testo \(p \ge 0{,}05\).
8. Nėra multikolinearumo problemos, dėl kurios neteisingai apskaičiuojami lygties koeficientai (tik daugialypei regresijai), jei:
   • regresijos koeficientų ženklai atitinka koreliacijos koef. ženklus tarp Y ir kiekvieno X;
   • visi \(VIF \le 4\) (VIF – dispersijos mažėjimo daugiklis, angl. variance inflation factor).
9. Nėra autokoreliacijos:
   • Tikriname tik tada, jei dirbame su laiko eilutėmis (pvz., mėnesiais, sekundėmis) arba dėl kitokių priežasčių įtariame, kad reikšmės gali būti priklausomos;
   • Durbin-Watson autokoreliacijos kriterijaus \(p\ge0{,}05\), kai alternatyva \(\varrho \ne 0\) (čia \(\varrho\) – (auto)koreliacijos koeficientas);
   • arba Durbin-Watson statistikos reikšmė yra tarp 1,5-2,5.

Jei turime daugialypę regresiją, papildomai apskaičiuojame standartizuotuosius (beta) koeficientus: kuo absoliučioji koeficiento vertė didesnė, tuo atitinkamas regresorius daro didesnę įtaką priklausomam kintamajam. Nestandartizuoti koeficientai tokios informacijos neteikia.

Analogišką (bet šiek tiek glaustesnį) apibendrinimą galite rasti regresijos vadovėlyje (Čekanavičius ir Murauskas 2014, p.36) . Pastabos:

• visi kintamieji regresinėje analizėje turi būti skaitiniai arba pseudokintamieji;
• regresijos vadovėlyje skaitiniai kintamieji vadinami intervaliniais;
• pseudokintamieji (angl. dummy variables) – tai kategoriniai kintamieji, tam tikru būdu perkoduoti į skaitinius. Kuriant tiesinės regresijos modelį „R“ tai atlieka automatiškai, todėl galite pamatyti neįprastai apibūdintų koeficientų, jei naudojate kategorinį kintamąjį;
• apie pseudokintamuosius šio kurso metu plačiau nesimokysime.

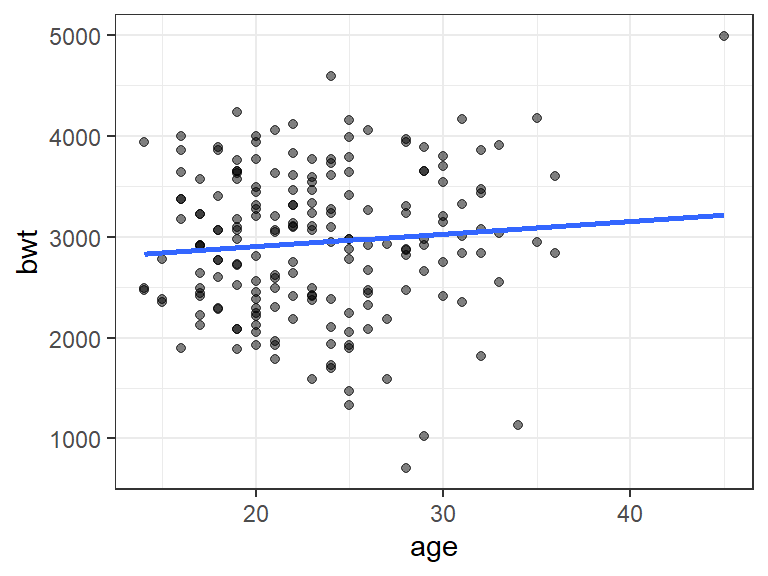
Pav. 21.1: Duomenų ir regresijos modelio atvaizdavimas sklaidos diagrama ir tiese.

21.4 Rezultatų aprašymas: tiesinė regresinė analizė

Aprašant tiesinės regresijos rezultatus įprasta nurodyti regresijos lygtį ir aprašyti kintamuosius, nurodyti determinacijos koeficientą \(R^2\) bei pateikti sklaidos diagramą su regresijos tiese. Standartinių tiesinės regresijos modelio aprašymų pavyzdžių galite rasti regresijos vadovėlio (Čekanavičius ir Murauskas 2014, p.40–41, 114) skyriuose:

• „2.1.8. Standartiniai tiesinės regresijos modelio aprašymai“ 40-41 psl.;
• „2.5.6. Išvados“ 114 psl.

21.5 Informacijos šaltiniai

Šiame konspekte itin glaustai pateikti tik esminiai regresinės analizės bruožai. Teorinė dalis išdėstyta šiuose vadovėliuose:

1. išdėstyti praktiniai modelio taikymo aspektai vengiant matematinių detalių (Čekanavičius ir Murauskas 2014, p.28–41, 127) ;
2. analizės pavyzdys naudojant „R“ (Čekanavičius ir Murauskas 2014, p.100–123);
3. matematiniai modelio aspektai (Čekanavičius ir Murauskas 2004, p.123–147, 151–179).

Papildomi informacijos šaltiniai, kuriuose mokoma, kaip interpretuoti regresinės analizės rezultatus:

1. Straipsnis, kuriame mokoma, kaip interpretuoti keturis pagrindinius tiesinės regresijos modelio diagnostikos grafikus (nuoroda );
2. Tinklaraščio straipsnis, kuriame supažindinama, kaip naudojantis R susidaryti tiesinės regresijos modelį ir kaip interpretuoti skaitinius modelio rezultatus (nuoroda );
3. Atsakymas diskusijų forume „Cross Validated“, kuriame aiškinama, kaip interpretuoti liekamųjų paklaidų pagal prognozuojamas reikšmes grafiką (nuoroda );
4. Atsakymas diskusijų forume „Cross Validated“, kuriame aiškinama, kaip interpretuoti liekamųjų paklaidų pagal įtakos indeksą grafiką (nuoroda ).

Mokomieji įrankiai:

1. Interaktyvus mokomasis įrankis Ordinary Least Squares Regression Explained Visually .