4. Skaitinės suvestinės
4.1 Aprašomoji statistika
Aprašomoji statistika – yra statistikos mokslo skyrius, kurio esmė yra susisteminti duomenis ir glaustai perteikti esminius jų bruožus. Tai atliekama pasitelkiant skaitines suvestines (statistinius koeficientus, rodiklius, lenteles) bei grafikus. Skyrius apie aprašomąją statistiką galite rasti vadovėliuose (Čekanavičius ir Murauskas 2006; Venclovienė 2010; Field ir kt. 2012).
4.2 Kompetencijos vykdant analizę
Šiame (ir kituose skyriuose) susipažinsime su įvairiais statistiniais analizės metodais, koeficientais, rodikliais, grafikais. Yra kelios pagrindinės su metodu susijusios kompetencijos:
- Parinkti: tinkamai situacijai pasirinkti tinkamą metodą ar rodiklį;
- Suprasti skaičiavimus: suprasti, kaip atliekami metodo skaičiavimai, t.y., kokia skaičiavimų matematika ir logika (ir bent jau paprasčiausius uždavinius mokėti patiems išspręsti „ranka“);
- Taikyti kompiuteriu: mokėti rodiklį apskaičiuoti bei metodą atlikti konkrečia kompiuterine programa;
- Suprasti rezultatus ir mokėti juos teisingai interpretuoti.
Tad analizuojant metodus patarčiau nepalikti „aklų dėmių“ ir metodą išmokti visapusiškai. Ši knyga skirta teorinei daliai apie rodiklius ir metodus, o kompiuterinių skaičiavimų dalis neįtraukta.
Tad dabar pereikime prie aprašomosios statistikos.
4.3 GA parametrai ir imties statistikos
Jeigu atliekant skaičiavimus naudojama visa generalinė aibė (GA), tada rezultatą – apskaičiuotąją GA charakteristiką – vadiname generalinės aibės parametru (pvz., GA vidurkis). Jei analogiškiems skaičiavimams naudojami imties duomenys, tada rezultatą – imties charakteristiką – vadiname imties statistika (pvz., imties vidurkis).
Terminu „skaitinės suvestinės“ vadinsime aprašomąsias statistikas, tokias kaip imties dydis, vidurkis, standartinis nuokrypis, dažnių lenteles ir kitus ne grafinius aprašomosios statistikos metodus (bei jų rezultatus).
Statistikomis vadinami dydžiai, apskaičiuoti iš imties duomenų (pvz., vidurkis).
4.4 Statistikų klasifikavimas
Imties statistikas galima skirstyti į kelias sąlygines grupes (pav. 4.1):

Pav. 4.1: Imties statistikų rūšys. Šiame skyriuje nagrinėsime aprašomąsias statistikas.
- Aprašomosios statistikos – charakteristikos, skirtos glaustai apibūdinti imties duomenis. Aprašomųjų statistikų pavyzdžių pateikta pav. 4.2.
- Įverčiai – tai, pagal turimus imties duomenis, geriausias spėjimas, koks yra tikrasis GA parametras (pvz., tikrasis vidurkis). Būna 2 rūšių:
- taškiniai įverčiai;
- intervaliniai įverčiai (pvz., pasikliautinieji intervalai).
- Statistinių kriterijų statistikos – tai dydžiai, kurių pagalba tikrinamos statistinės hipotezės ir daromos statistinės išvados (pvz., t statistika Stjudento t teste).
4.5 Suvestinės vienam kintamajam
Svarbiausios vieną kintamąjį aprašančios statistikos ir kitos skaitinės suvestinės pateiktos pav. 4.2.
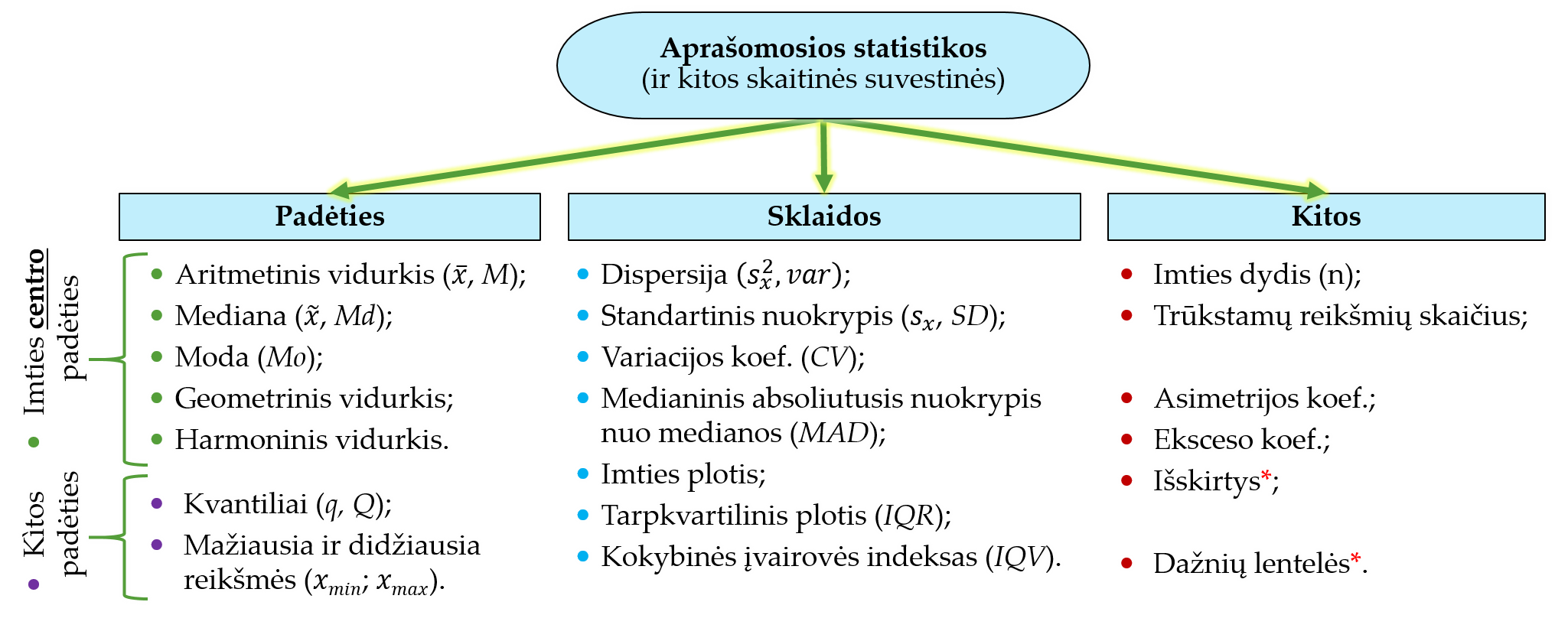
Pav. 4.2: Aprašomųjų statistikų ir kitų skaitinių suvestinių pavyzdžiai.
* – kitos suvestinės.
Keletas svarbių sąvokų:
- Imties dydis – tai imtyje esančių elementų (pvz., tiriamųjų, pacientų ar pan.) skaičius. Matematinėje statistikoje dar vadinamas imties tūriu.
- Sakykime, respondentas atsisakė atsakyti į klausimą, prietaisas, atlikęs keletą tyrimų, sugedo ar dėl kitokių priežasčių dalies duomenų negavome ar praradome. Tokios negautos duomenų reikšmės vadinamos praleistomis arba trūkstamomis reikšmėmis (angl. missing values). Dažnai tyrimuose žymimos
NA(angl. not available) arba kitu specialiuoju simboliu. - Empirinis kintamojo reikšmių pasiskirstymas, arba skirstinys (angl. distribution), – tai apibūdinimas, kiek kokių kintamojo reikšmių yra ir kaip tos reikšmės išsidėsto pagal pasitaikymo dažnumą: kurios – dažniausiai, kurios – rečiau, o kurių – apskritai nėra, ar reikšmių pasitaikymo dažnumas vidurkio atžvilgiu yra simetriškas, ar nėra pavienių ženkliai nuo duomenų centro nutolusių reikšmių ir pan.
- Statistinis dažnis (angl. frequency) parodo, kaip dažnai reikšmė pasitaiko duomenų eilutėje.
- Dažnių lentelė (angl. frequency table) parodo, kaip dažnai kiekviena iš reikšmių pasitaiko arba kaip dažnai patenka į tam tikrą reikšmių intervalą.
- Jei duomenis norime atvaizduoti dažnių lentele, skaitinės reikšmės gali būti grupuojamos į pasirinktus intervalus. Reikšmių grupavimas į intervalus angliškai vadinamas binning, tokio tipo intervalas – bin. O iš tokių duomenų sudaryta lentelė – grupuotųjų duomenų dažnių lentelė.
- Išskirtis – tai reikšmė (pvz., grafiko taškas), „išsiskirianti iš bendrosios masės“. Išskirtimis taip pat galima pavadinti taškus, kurie smarkiai nesiderina su mūsų pasirinktu statistiniu modeliu. Tai taškai, kuriems reiktų skirti dėmesio išsiaiškinti, ar tai duomenų surinkimo klaidos, ar iš tiesų neįprastos realiai egzistuojančios reikšmės. Terminas „išskirtis“ pats savaime nerodo, kad šį tašką reiktų pašalinti.
Imties dydis – tai statistika, kurią privaloma nurodyti kiekvienoje duomenų analizės ataskaitoje.
4.5.2 Kvantiliai ir kvartiliai
Kvantiliai – tai duomenų padėtį apibūdinančios charakteristikos.
Imties \(\beta\)-tosios eilės kvantilis (pažymėkime raide \(q\), o \(\beta \in [0; 1]\)) – yra konkreti duomenų eilutės reikšmė (arba dviejų reikšmių funkcija), kuri pagal imties dydį variacinę eilutę dalina į dvi dalis: vienoje yra daugmaž \(\beta\), kitoje – \((1-\beta)\) narių. Čia \(\beta\) yra dalis – skaičius tarp 0 ir 1 \((0 < \beta < 1)\). Atkreipkite dėmesį, kad kvantilis matuojamas tais pačiais matavimo vienetais, kaip ir tiriamieji duomenys: jei matuojame ilgį centimetrais, tai kvantilis yra tam tikras ilgis centimetrais, jei masę kilogramais, tai ir kvantilis bus tam tikra masė kilogramais. Pvz., jei kvantilis \(q_{\beta=0{,}2} = 35 \mu m\) (įprastai bus žymimas tiesiog \(q_{0{,}2} = 35 \mu m\)), tai reiškia, kad 20% mūsų imtyje esančių tiriamųjų yra mažesni už \(35 \mu m\) ir 80% didesni už šį kvantilį. Tai pat pastebėkite, jog skaičius \(\beta\) šalia kvantilio nurodo, kuri imties narių dalis yra mažesnė už kvantilio reikšmę.
Kvantilis \(q_{0.5}\) yra plačiausiai naudojamas ir turi specialų pavadinimą – mediana \((Md)\). Tai skaičius, variacinę eilutę dalinantis į dvi lygias dalis santykiu 50%:50%.
Kvartiliai – tai kvantiliai, dalijantys variacinę duomenų eilutę į 4 lygias dalis. Įprastai žymimi \(Q_1\), \(Md\), \(Q_3\).
4.5.4 Duomenų formos charakteristikos
Yra dvi pagrindinės duomenų formą aprašančios statistikos:
- Asimetrijos koeficientas, \(g_1\) (angl. skewness, trumpinama skew) – vertina skirstinio simetriškumą. Koeficiento ženklas nurodo asimetrijos kryptį:
- \(g_1 = 0\) – ideali simetrija;
- \(g_1 < 0\) – neigiama (kairioji) asimetrija;
- \(g_1 > 0\) – teigiama (dešinioji) asimetrija. Pastarąją galima bandyti koreguoti logaritmuojant.
- \(g_1 = 0\) – ideali simetrija;
- \(|g_1| < 0{,}5\) – maža asimetrija, beveik simetriška;
- \(0{,}5 < |g_1| < 1\) – vidutinio stiprumo asimetrija;
- \(1 < |g_1|\) – stipri asimetrija.
- Eksceso koeficientas (nedetalizuosime).
4.5.5 Statistinis dažnis ir dažnių lentelės
Kintamojo reikšmės dažnis \(f_i\) – tai skaičius, nurodantis, kiek kartų reikšmė \(x_i\) pasikartojo duomenų eilutėje. Kinta intervale nuo 0 iki \(+\infty\).
Kintamojo reikšmės santykinis dažnis \(\frac {f_i}{n}\) – tai skaičius, nurodantis, kurią duomenų eilutės dalį sudaro reikšmė \(x_i\). Įprastai tai skaičius tarp 0 ir 1 \(\left(0 \le \frac{f_i}{n} \le 1 \right)\). Gali būti išreikštas ir procentais. Čia \(n\) – visų elementų skaičius (imties dydis).
Kintamojo reikšmių dažnių lentelėse nurodoma, kiek kartų kiekviena diskrečiojo ar kategorinio kintamojo reikšmė pasikartojo.
Dažnių lentelės – tai pagrindinis kategorinių duomenų statistinio apibendrinimo būdas.
| Spalva | Skaičius | Dalis |
|---|---|---|
| Juoda | 35 | 0.354 |
| Žalia | 11 | 0.111 |
| Geltona | 30 | 0.303 |
| Raudona | 23 | 0.232 |
* – Lentelėje pateikti absoliutieji ir santykiniai dažniai.
4.5.6 Kaip statistiškai aprašyti vieno kintamojo reikšmes?
Prieš atliekant vieno kintamojo suvestines, reikia nustatyti kintamojo duomenų tipą. Panagrinėkime du kraštutinumus – nominaliuosius ir tolydžiuosius duomenis. Šiais atvejais – įprasti tokie pasirinkimai:
- Kategoriniams nominaliesiems duomenims pateikiama:
- imties dydis;
- dažnių lentelė.
- Tolydiesiems duomenims:
- imties dydis;
- duomenų centras (įprastai vidurkis arba mediana);
- duomenų sklaida (įprastai SD, kvartiliai Q1, Q3, IQR arba MAD).
Jei duomenys ranginiai arba skaitiniai diskretieji, jiems gali tikti ir tolydžiųjų, ir diskrečiųjų duomenų aprašymo metodai. Įvertinus, į ką – tolydžiuosius (t.y., kiekybinius) ar diskrečiuosius (t.y., nominaliuosius) duomenis – konkretus kintamasis panašesnis, parenkamas aprašomosios statistikos metodas. Įprasti pasirinkimai:
- Ranginiams duomenims:
- imties dydis*;
- dažnių lentelė*;
- mediana;
- kiti centrą (pvz., vidurkis) ir sklaidą (pvz., SD) aprašantys dydžiai naudojami tik tada, jei jie turi prasmę.
- Diskretiesiems skaitiniams duomenims:
- imties dydis;
- duomenų centras;
- duomenų sklaida;
- dažnių lentelė (įprasta tik tada, kai skirtingų reikšmių yra mažai).
* – privaloma.
4.5.7 Kaip pasirinkti kiekybiniams duomenims tinkamas suvestines?
Kai jau nustatėme, kad duomenys yra kiekybiniai (pvz., tolydieji), toliau žiūrime į duomenų pasiskirstymo formą ir įvertiname, ar yra išskirčių. Tokiu būdu nustatome, kokios statistikos geriausiai apibūdina duomenų centrą ir sklaidą (išsidėstymą apie tą centrą):
- Jei duomenys simetriški ir be ryškių išskirčių, įprastai centrui apibūdinti naudojamas aritmetinis vidurkis ir sklaidai – standartinis nuokrypis (SD).
- Jei duomenys smarkiai asimetriški arba turi ryškių išskirčių, labiau tinka išskirtims ir nukrypimams atsparios (robastiškos) statistikos: centrui – mediana, sklaidai – kvartiliai, MAD (medianinis absoliutusis nuokrypis nuo medianos), IQR (tarpkvartilinis plotis).
Galutinėje ataskaitoje tyrėjo nuožiūra pasirenkamas vienas labiausiai tinkantis centro padėties ir vienas sklaidos aprašymo būdas. Taip pat nurodomas ir imties dydis.
Statistiškai aprašant tolydžiuosius (kiekybinius) duomenis įprasta apibūdinti imties dydį, duomenų centro padėtį ir sklaidą.
4.5.8 Z reikšmės
Z reikšmė gaunama iš pradinės duomenų reikšmės atėmus vidurkį ir padalinus iš standartinio nuokrypio. Tai z transformacija, dar vadinama standartizavimu:
\[\begin{equation} z_i = \frac{x_i - \overline{x}}{s_x} \tag{4.13} \end{equation}\]
Z reikšmė parodo, kiek standartinių nuokrypių reikšmė yra nutolusi nuo vidurkio. Gali būti tiek teigiamas (jei nuokrypis į didesnių), tiek neigiamas dydis (jei nuokrypis į mažesnių reikšmių pusę).
4.6 Suvestinės kintamųjų porai
Sakykime, kad tiriame kintamųjų porą. Į duomenų lentelę ją įrašome kaip du stulpelius. Pačiu paprasčiausiu atveju, turint du vienos rūšies (abu tolydieji arba abu nominalieji) kintamuosius skaičiuojamas statistinio ryšio tarp kintamųjų stiprumas, o turint du skirtingų rūšių (vienas – tolydusis, kitas – nominalusis) – įprastai skaičiuojamas skirtumas tarp pogrupių centro padėčių. Jei tarp kintamųjų ryšys yra, tai reiškia, kad žinodami vieno kintamojo reikšmę, gauname informacijos ir apie galimą antro kintamojo reikšmę. Jei ryšio nėra – apie antrojo kintamojo reikšmę jokios informacijos negauname.
4.6.1 Du kiekybiniai kintamieji
Kovariacijos koeficientas tarp 2 kintamųjų, arba tiesiog kovariacija \((cov)\), tai dydis, parodantis, kaip kintant vieno kintamojo reikšmėms kinta kito kintamojo reikšmės. Imties duomenims apibrėžiama taip (žymėjimas \(_{xy}\) rodo, kad kovariaciją skaičiuojame tarp kintamųjų \(x\) ir \(y\)):
\[\begin{equation} cov_{xy} = \frac{1}{n-1} \sum_{i=1}^n {(x-\overline{x})(y-\overline{y})} \tag{4.14} \end{equation}\]
Trūkumas – kovariacijos matavimo vienetai priklauso nuo duomenų matavimo vienetų, todėl skirtingais vienetais matuojamiems dydžiams kovariacijos koeficiento verčių korektiškai palyginti neįmanoma. Kovariaciją standartizavę pagal kintamųjų standartinius nuokrypius gauname bedimensį dydį. Tai Pearson (Pirsono) tiesinės koreliacijos koeficientas \((r)\):
\[\begin{equation} r_{xy} = \frac{ cov_{xy} }{ s_x ~ s_y } \tag{4.15} \end{equation}\]
Arba:
\[\begin{equation} r_{xy} = \frac{\sum{(x-\overline{x})(y-\overline{y})}} {\sqrt{\sum{(x-\overline{x})^2}} \sqrt{\sum{(y-\overline{y})^2}}} \tag{4.16} \end{equation}\]
Koeficientą galima apibrėžti ir kaip sandaugą tarp z reikšmių sumų: \[\begin{equation} \begin{aligned} r_{xy} = \\ & = \frac{1}{n-1} \sum_{i=1}^n \left( \frac{x_i - \overline{x}}{s_x} \right) \sum_{i=1}^n \left( \frac{y_i - \overline{y}}{s_y} \right) \\ & = \frac{1}{n-1} \sum_{i=1}^n z_{xi} \sum_{i=1}^n z_{yi} \end{aligned} \tag{4.17} \end{equation}\]
Koreliacijos koeficientas kinta nuo -1 iki 1:
- \(0\) reiškia, kad ryšio nėra;
- \(-1\) – visiška atvirkštinė priklausomybė (vieno kintamojo reikšmėms didėjant, kito – mažėja);
- \(+1\) – visiška tiesioginė priklausomybė (vieno kintamojo reikšmėms didėjant, kito irgi didėja).
Pearson koreliacija tinkama, kai ryšys tarp kintamųjų tiesinis. Be tiesinės, dažnai naudojami ir ranginės koreliacijos koeficientai: Spearman \(r_s\) arba Kendall \(\tau\) (tau). Jie tinkami, kai ryšys tarp kintamųjų netiesinis, bet monotoninis (nedidėjantis arba nemažėjantis).
Plačiau koreliacinė analizė nagrinėjama skyriuje „20 Koreliacinė analizė: ryšys tarp kintamųjų“.
4.6.2 Porinės dažnių lentelės
Jei turime du nominaliuosius kintamuosius (t.y., kintamųjų porą), jų analizė pradedama sudarant porinę dažnių lentelę 1 (angl. cross-tabulation arba contingency table). Pavyzdys, kuriame pateikti tik absoliutieji dažniai:
| Rūko | Serga | Taip | Ne |
| Taip | 125 | 173 | |
| Ne | 99 | 603 |
Sudėtingesnis porinės dažnių lentelės pavyzdys, kurioje yra eilučių procentinė dalis, stulpelių ir eilučių sumos, praleistų reikšmių (<NA>) skaičius.
| Rūko | Lytis | M | V | <NA> | Suma |
| Taip | 147 (49.3%) | 143 (48.0%) | 8 (2.7%) | 298 (100.0%) | |
| Ne | 342 (48.7%) | 346 (49.3%) | 14 (2.0%) | 702 (100.0%) | |
| Suma | 489 (48.9%) | 489 (48.9%) | 22 (2.2%) | 1000 (100.0%) |
Dar vienas dažnių lentelės pavyzdys, kuriame pateikti absoliutieji dažniai (freq), bendroji (perc), eilučių (p.row) ir stulpelių (p.col) procentinės dalys.
gender F M NA Sum
smoker
Yes freq 147 143 8 298
perc 14.7% 14.3% 0.8% 29.8%
p.row 49.3% 48.0% 2.7% .
p.col 30.1% 29.2% 36.4% .
No freq 342 346 14 702
perc 34.2% 34.6% 1.4% 70.2%
p.row 48.7% 49.3% 2.0% .
p.col 69.9% 70.8% 63.6% .
Sum freq 489 489 22 1'000
perc 48.9% 48.9% 2.2% 100.0%
p.row . . . .
p.col . . . .
4.6.3 Ryšys tarp nominaliųjų kintamųjų
Ryšys tarp nominaliųjų kintamųjų gali būti matuojamas įvairiais koeficientais. Čia aptarsime kelis:
- Cramer V
- Goodman-Kruskal τ
- Goodman-Kruskal λ
Cramer V
Vienas iš galimų būdų įvertinti ryšio tarp dviejų kategorinių kintamųjų stiprumą – skaičiuoti Kramerio V koeficientą (angl. Cramer’s V). Šis koeficientas kinta:
- nuo 0, kai ryšio nėra;
- iki 1, kai tarp kintamųjų visiška priklausomybė.
Sakykime, jau turime porinę dažnių lentelę. Iš jos apsiskaičiuojame \(\chi^2\) (chi kvadratu) statistiką:
\[\begin{equation} \chi^2 = \sum^c_{i=1} \sum^r_{j=1} \frac { \left(n_{ij} - \frac{n_{i.} ~ n_{.j}} {n}\right)^2} { \frac {n_{i.} ~ n_{.j}} n } \tag{4.18} \end{equation}\]
Čia \(i\) ir \(j\) – eilutės ir stulpelio numeriai, \(r\) ir \(c\) – eilučių ir stulpelių skaičius, \(n_{i.}\) – \(i\)-tosios eilutės bei \(n_{.j}\) – \(j\)-ojo stulpelio dažnių suma, \(n_{ij}\) – \(i\) eilutėje ir \(j\) stulpelyje esančio langelio absoliutusis dažnis (empirinis dažnis), \(n\) – imties dydis. Pažymėjimas \(\frac{n_{i.} ~ n_{.j}}{n}\) yra tikėtinas (teorinis) dažnis.
Tada \(V\) gaunamas:
\[\begin{equation} V={\sqrt{ \frac{ \chi^2 / n }{ \min(c-1, ~ r-1) }}} \tag{4.19} \end{equation}\]
Koeficientas yra simetriškas: jei sukeisime kintamuosius vietomis, gausime tokią pačią koeficiento V reikšmę. Visgi koeficiento trūkumas yra neaiški tikimybinė skaitinės reikšmės interpretacija.
Goodman-Kruskal τ ir λ
Gudmano-Kraskalo (Goodman-Kruskal) koeficientai τ (tau) ir λ (lambda) taip pat naudojami ryšio tarp nominaliųjų kintamųjų stiprumui vertinti. Šie koeficientai iš principo parodo tą patį – kiek sumažėja klaida atspėti vieno (atsako) kintamojo reikšmę, pagal kito (aiškinamojo) kintamojo reikšmę lyginant su visiškai atsitiktiniu spėjimu. Tik koeficientų apskaičiavimo procedūros skiriasi (Minitab 21 Support 2021). Dėl skaičiavimų specifikos (atsiradusio nulio dalyboje), kai kuriais atvejais λ koeficiento reikšmė tampa lygi nuliui, nors neturėtų. Dėl šios priežasties labiau rekomenduočiau naudoti τ koeficientą.
Abu koeficientai kinta nuo 0 iki 1:
- 0 rodo, kad ryšio nėra (klaidos sumažėjimas 0%),
- 1 – kad visiška priklausomybė (klaidos sumažėjimas 100%).
Koeficientai τ ir λ yra asimetriški: jei dažnių lentelės eilučių ir stulpelių skaičius skiriasi, tai sukeitę kintamuosius vietomis gausime kitokią skaitinę reikšmę.
Yra ir daugiau metodų ryšio tarp kategorinių kintamųjų stiprumui vertinti.
Yra ir daugiau metodų ryšio tarp kategorinių kintamųjų stiprumui vertinti. Vienas iš jų – taip pat vertas dėmesio ir kai kuriose jo interpretacija netgi lengviau suvokiama nei anksčiau minėtųjų – yra galimybių (šansų) santykis, naudojamas 2×2 dažnių lentelėms. Šiame skyriuje jis nėra aptartas.
Informacijos šaltiniai
Porinė dažnių lentelė dar vadinama sąveikos lentele (Čekanavičius ir Murauskas 2006, p.49).↩︎
{target="_blank"}).](https://onlinestatbook.com/2/summarizing_distributions/graphics/balance1.jpg)