10. Pasikliautinieji intervalai (PI)

10.1.1 Statistikos skirstinys

Kalbant apie skirstinius, pagal tai, kieno tai skirstinys, mes galime turėti kelių „lygių“ skirstinius (pav. 10.1):

1. Generalinės aibės reikšmių skirstinys (angl. population distribution) – įprastai mes jo nežinome, todėl ir atliekame tyrimą.
2. Imties reikšmių skirstinys (angl. sample distribution) – tai į tyrimą patekusių tiriamųjų savybių reikšmių skirstinys.
3. Imties statistikų skirstinys (angl. sampling distribution) – jeigu sudarytume daug atsitiktinių imčių ir skaičiuotume jų vidurkius, tai kiekvienai imčiai turėtume po vidurkį. Vadinasi, galėtume sudaryti vidurkių skirstinį – tai ir būtų vienas iš imties statistikų pavyzdžių.
4. Pakartotinės atrankos (pvz., savirankos) metodu sudarytas statistikų skirstinys (angl. resampling distribution). Apie jį plačiau pakalbėsime skyriuje „10.4 Savirankos metodai“.

Pav. 10.1: Simuliacija: generalinės aibės, imties ir imties statistikos (vidurkio) skirstiniai. Juodi pilnaviduriai taškai vaizduoja į imtį patekusius elementus. Šaltinis .

Darant statistines išvadas, imtis turi būti atsitiktinė. Dėl šios priežasties kiekviena statistika, skaičiuota iš tokios imties, taip pat yra atsitiktinis dydis. Kiekvienas atsitiktinis dydis turi skirstinį. Pagal šį skirstinį ir yra vertinamos pasikliautinojo intervalo ribos. Klasikiniais vadinsime tuos metodus, kai statistikų skirstinys, pagal kurį skaičiuojami PI, yra aproksimuotas naudojant analitiškai išvestą formulę. Savirankos metodai statistikų skirstinį sudaro imties duomenims vykdydami daugybę perskaičiavimų.

10.1.2 PI „anatomija“

Pasikliautinąjį intervalą sudaro apatinė ir viršutinė ribos, dar vadinamos rėžiais (pažymėkime \(\hat{\theta}_{apatinis}\) ir \(\hat{\theta}_{viršutinis}\)). Norint sudaryti pasikliautinuosius intervalus, įprastai reikia žinoti taškinį statistikos įvertį (pažymėkime \(\hat{\theta}\)) ir prie jo pridėti bei iš jo atimti paklaidą.

\[\begin{equation} \hat{\theta}_{apatinis} = \hat{\theta} - paklaida_1 \\ \hat{\theta}_{viršutinis} = \hat{\theta} + paklaida_2 \tag{10.1} \end{equation}\]

Bendruoju atveju, taškinio įverčio atžvilgiu PI nebūtinai turi būti simetriški. Be to, yra metodų, kai PI įvertinimui taškinį įvertį žinoti nėra būtina. Visgi, atvaizduojant ir aprašant PI įprasta nurodyti tiek taškinį įvertį, tiek PI rėžius.

10.1.3 PI apibrėžimas

Praktikoje dažniausiai skaičiuojami 95% pasikliautinieji intervalai. Jie apibrėžiami taip: jei iš generalinės aibės imtume be galo daug atsitiktinių imčių (t.y., jei daug kartų kartotume tyrimą sudarydami vis naujas imtis) ir pagal jas sudarytume tam tikro parametro (sakykime, vidurkio) PI, tai maždaug 95 atvejais iš 100 PI būtų sudarytas taip, kad tarp jo ribų patektų ir tikroji parametro (pvz., generalinės aibės vidurkio \(\mu\)) reikšmė.

Su PI susijusi sąvoka – pasikliovimo lygmuo Q. Iš principo, tai tikimybė, rodanti, kaip dažnai intervalai būna sudaromi teisingai, jei naudojame tam tikrą PI sudarymo metodą. Kitais žodžiais kalbant, Q parodo mūsų pasitikėjimą PI sudarymo metodu (pav. 10.2).

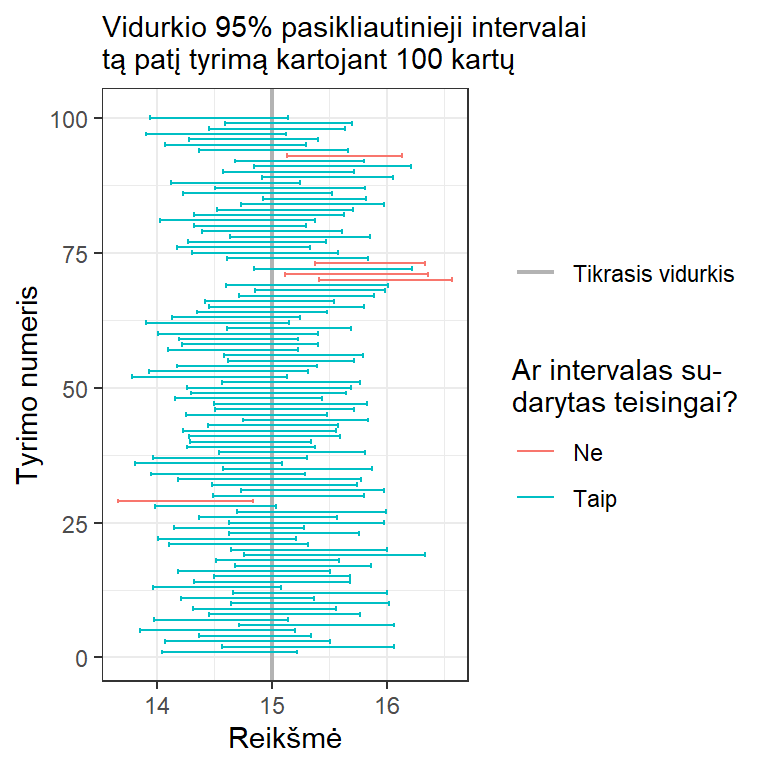
Pav. 10.2: Jei skaičiuojame 95% pasikliautinuosius intervalus, tai maždaug 95 atvejais iš 100 intervalai bus sudaryti teisingai (melsvos linijos). Tie 95% parodo mūsų pasitikėjimą intervalų sudarymo taisykle.

Apie tai, kas yra pasikliautinieji intervalai, plačiau paaiškinta šaltinio (Čekanavičius ir Murauskas 2014, p.25) skyriuje „Parametrų įverčiai ir jų pasikliautinieji intervalai“ (skyrius trumpas, rekomenduoju perskaityti).

10.2.1 Vidurkio PI, kai GA dispersija žinoma ar imtis didelė

Kai duomenys – normalieji, o generalinės aibės dispersija žinoma, vidurkio PI galima skaičiuoti pagal formulę (10.2). Situacija, kai tikrasis vidurkis nežinomas, o duomenų išsisklaidymas aplink jį (dispersija) – žinomas, įprastai yra tik hipotetinė. Tačiau formulė ganėtinai paprasta ir mokymosi tikslais iliustruoti, kaip konstruojamas PI, tinkama. Ši formulė taip pat naudojama ir tada, kai imties dydis pakankamai didelis (vienų autorių teigimu, bent 30, kitų – bent 50).

Ši formulė tinka normaliai pasiskirsčiusiems duomenims arba duomenims, kurių yra tiek daug, kad centrinė ribinė teorema ima veikti pakankamai smarkiai. (Centrinė ribinė teorema teigia, kad kuo didesnė imtis, tuo labiau jos vidurkio skirstinys supanašėja su normaliuoju.)

\[\begin{equation} \hat{\mu}_{1,2} = \overline{x} \mp z_{\left(\frac{1-Q}{2}\right)}{\sigma \over \sqrt{n}} \tag{10.2} \end{equation}\]

Formulėje:
\(\hat{\mu}_{1}\) – apatinė vidurkio pasikliautinojo intervalo riba (mažesnis skaičius);
\(\hat{\mu}_{2}\) – viršutinė vidurkio pasikliautinojo intervalo riba (didesnis skaičius);
\(\overline{x}\) – imties reikšmių vidurkis;
\(\sigma\) – generalinės aibės standartinis nuokrypis (arba imties standartinis nuokrypis, jei duomenų pakankamai daug);
\(n\) – imties dydis;
\(Q\) – pasikliovimo lygmuo (tikimybė: skaičius tarp 0 ir 1, įprastai – 0,95);
\({\left(\frac{1-Q}{2}\right)}\) – galime pažymėti kaip tikimybę \(\alpha^*\);
\(z_{\alpha^*}\) – \(z\) koeficientas – daugiklis, dar vadinamas standartinio normaliojo skirstinio \(1-\alpha^*\) lygmens kvantiliu (skaičius, priklausantis nuo norimo pasikliovimo lygmens). Jis imamas iš lentelių arba apskaičiuojamas programomis „R“, „GeoGebra“ (pav. 10.3) ar kitomis.

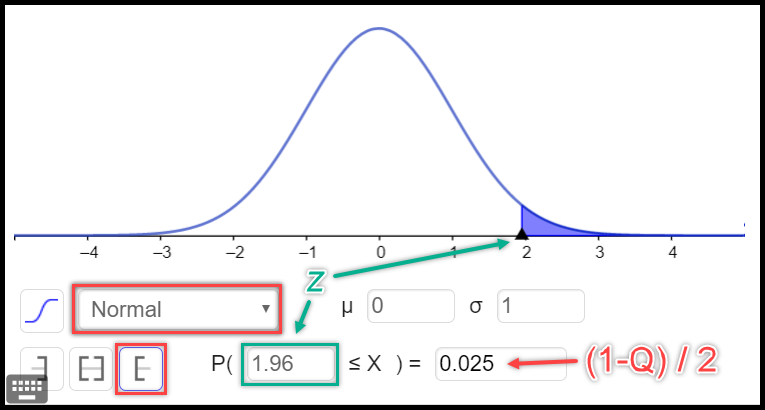
Pav. 10.3: Koeficiento \(z\) skaičiavimas programa „GeoGebra“. Naudojamas standartinis normalusis skirstinys. Koeficiento reikšmė nuo imties dydžio nepriklauso. Q – pasikliovimo lygmuo. Žalsva spalva pažymėta vieta, kur gauname atsakymą (\(z\) koeficientą), kai teisingai užpildome visus kitus laukelius.

Siekiant apsiskaičiuoti reikiamą imties dydį, kad būtų pasiektas norimas tikslumas (intervalo ilgis), gali būti naudojama iš (10.2) formulės išvesta lygtis (10.4).

Mažoms normaliai pasiskirsčiusioms imtims taikoma kita formulė, kurioje naudojamas \(t\) koeficientas (žr. 10.2.2 skyriuje).

10.2.2 Vidurkio PI, kai GA dispersija nežinoma

Kai GA dispersija nežinoma, tada vidurkio PI skaičiavimo formulėje naudojame iš duomenų apskaičiuotą dispersiją. Tokiu atveju vietoje \(z\) koeficiento reikia naudoti \(t\) koeficientą, kurio dydis priklauso nuo imties dydžio. Tad formulė (10.3) įprastai yra tinkamesnė, kai analizuojame mūsų pačių surinktus duomenis. Ši formulė tinka normaliai pasiskirsčiusiems duomenims, arba duomenims, kurių yra tiek daug, kad ima veikti centrinė ribinė teorema. (Centrinė ribinė teorema teigia, kad kuo didesnė imtis, tuo labiau jos vidurkio skirstinys supanašėja su normaliuoju.)

\[\begin{equation} \hat{\mu}_{1,2} = \overline{x} \mp t_{\left(\frac{1-Q}{2}\right)}^{(n-1)} {s \over \sqrt{n}} \tag{10.3} \end{equation}\]

Formulėje:
\(\hat{\mu}_{1}\) – apatinė vidurkio pasikliautinojo intervalo riba (mažesnis skaičius);
\(\hat{\mu}_{2}\) – viršutinė vidurkio pasikliautinojo intervalo riba (didesnis skaičius);
\(\overline{x}\) – imties reikšmių vidurkis;
\(s\) – imties reikšmių standartinis nuokrypis;
\(n\) – imties dydis;
\(Q\) – pasikliovimo lygmuo (tikimybė: skaičius tarp 0 ir 1, įprastai 0,95);
\({\left(\frac{1-Q}{2}\right)}\) – galime pažymėti kaip tikimybę \(\alpha^*\);
\(t_{\alpha^*}^{(n-1)}\) – daugiklis, dar vadinamas Stjudento koeficientu arba Stjudento skirstinio (su \(n-1\) laisvės laipsnių) \(1-\alpha^*\) lygmens kvantiliu (skaičius, priklausantis nuo norimo pasikliovimo lygmens). Jis imamas iš lentelių arba apskaičiuojamas programomis „R“, „GeoGebra“ (pav. 10.4) ar kitomis.

Ši formulė tinka normaliai pasiskirsčiusiems duomenims, arba duomenims, kurių yra tiek daug, kad ima veikti centrinė ribinė teorema. (Centrinė ribinė teorema teigia, kad kuo didesnė imtis, tuo labiau jos vidurkio skirstinys supanašėja su normaliuoju.) Jei skaičiavimus atliekame imties duomenims, formulė su \(t\) koeficientu yra universalesnė: tinka ir tada, kai imtis maža. Jei taškų yra iki 15 – pasiskirstymas privalo būti idealiai normalusis. Pastaba: kai imtis mažesnė nei 20, statistinių normalumo prielaidos tikrinimo metodų (žr. 16 skyriuje) rezultatai yra nepatikimi.

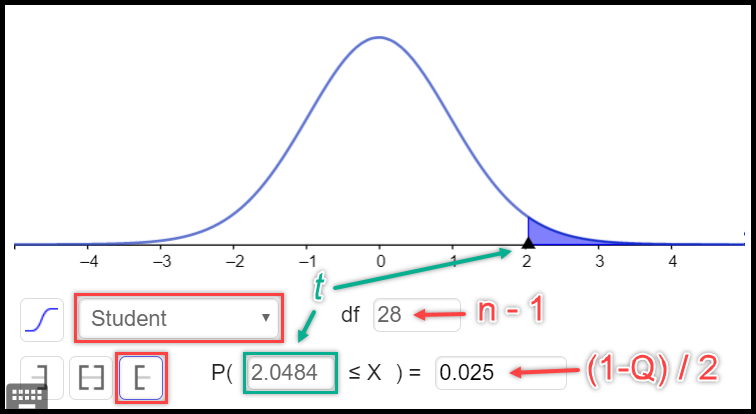
Pav. 10.4: Koeficiento \(t\) skaičiavimas programa „GeoGebra“. Naudojamas Stjudento skirstinys, kurio forma priklauso nuo imties dydžio (n). Q – pasikliovimo lygmuo. Žalsva spalva pažymėta vieta, kur gauname atsakymą (\(t\) koeficientą), kai teisingai užpildome visus kitus laukelius.

10.2.3 Imties dydžio skaičiavimas norimam vidurkio PI ilgiui

Jei norime apskaičiuoti reikiamą imties dydį, kurio reikia norimam tikslumui pasiekti, tai padaryti iš formulės su \(t\) koeficientu (10.3) yra ganėtinai sudėtinga. Todėl tokiai situacijai įprastai naudojama formulė su \(z\) koeficientu (10.2), kurio reikšmė nepriklauso nuo imties dydžio. Iš formulės išreikštą imties dydį aprašo lygtis (10.4):

\[\begin{equation} n = \left( {2 \cdot \sigma\cdot z_{\left(\frac{1-Q}{2}\right)} } \over \Delta\hat{\mu} \right)^2 \tag{10.4} \end{equation}\]

Formulėje:
\(n\) – imties dydis;
\(\Delta\hat{\mu}\) – vidurkio pasikliautinojo intervalo ilgis;
\(\sigma\) – (hipotetinis) standartinis nuokrypis;
\(Q\) – pasikliovimo lygmuo (tikimybė);
\({\left(\frac{1-Q}{2}\right)}\) – galime pažymėti kaip tikimybę \(\alpha\);
\(z_{\alpha}\) – \(z\) koeficientas – daugiklis, dar vadinamas standartinio normaliojo skirstinio \(1-\alpha\) lygmens kvantiliu (skaičius, priklausantis nuo norimo pasikliovimo lygmens).

Rezultatą apvaliname iki sveikųjų skaičių į didesnių reikšmių pusę, tarkime, 60,02 → 61. Kitu atveju intervalas bus per trumpas (t.y., nebus pasiektas norimas tikslumas).

10.4.1 Savirankos metodai ir imties dydis

Savirankos metodai tinka ir mažoms imtims. Visgi, imties dydis turėtų būti pakankamai didelis, pvz., 20 ar daugiau tiriamųjų/stebėjimų kiekviename pogrupyje, kuriam skaičiuojamas PI. Kitu atveju gali būti gauti klaidingi rezultatai (įprastai pernelyg siauras intervalas) dėl mažo imties dydžio ir nepakankamai reprezentatyvios imties. Jei jūsų imtis itin maža, siūlau temą apie savirankos metodą ir imties dydį panagrinėti išsamiau.

10.4.2 Baziniai principai

I etapas. Iš turimos duomenų imties (o ne visos generalinės aibės, GA) pakartotinai imame imtis grąžintiniu imties sudarymo būdu – vykdome pakartotinę atranką (pakartotinai atrenkame, t.y., sudarome, imtis). Jas vadinkime pakartotinėmis imtimis (angl. resamples). Stabiliam rezultatui pasiekti įprastai reikia \(10^3\)-\(10^4\) tokių imčių. Kiekvienos jų dydis toks, kaip pradinės imties (\(n\)).

II etapas. Kiekvienai pakartotinei imčiai apskaičiuojame mus dominančios statistikos (pvz., vidurkio) įvertį: kiek yra imčių, tiek bus ir vidurkio įverčių, kurie šiek tiek tarpusavyje skiriasi. Tad sudaromas statistikų skirstinys (pav. 10.7). Šiame etape reiktų įvertinti, ar skirstinys yra normalusis, ar simetriškas, ir pagal tai pasirinkti tolimesnius analizės metodus.

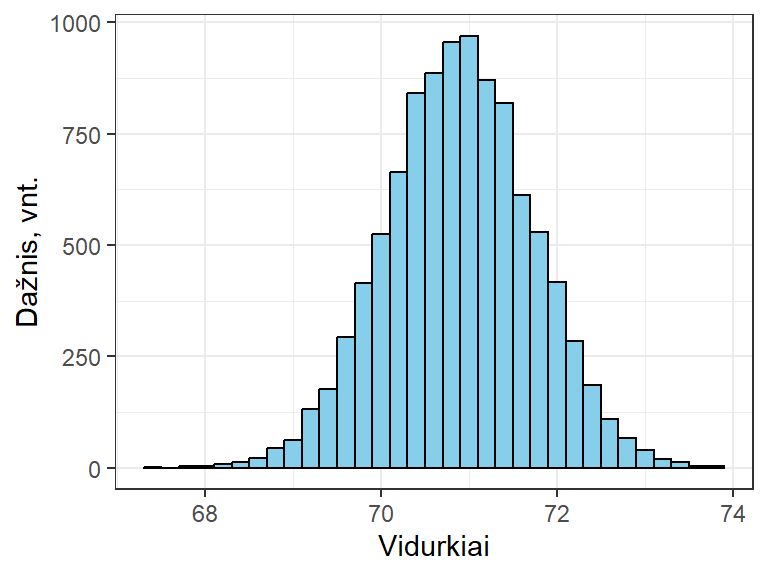
Pav. 10.7: Savirankos metodu apskaičiuotų tūkstančio vidurkių skirstinys (pavyzdys).

III etapas Pagal statistikų skirstinį apskaičiuojamos PI ribos. Tam gali būti naudojami keli metodai. Panagrinėkime du:

1. Procentilių metodą.
2. Koreguotąjį procentilių metodą \((BC_a)\).

Jei skirstinys yra normalusis ir žinome, kad statistika yra nepaslinktoji (pvz., vidurkis), galime naudoti patį paprasčiausią – procentilių metodą. Tiesiog apskaičiuojame skirstinio procentilius ties 2,5% ir 97,5% (tarp jų kaip tik telpa 95%) – tai ir bus PI ribos.

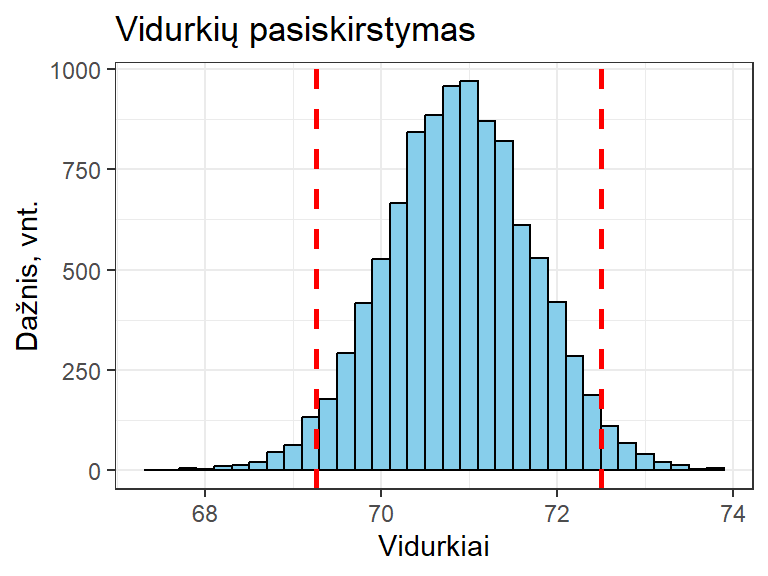
Pav. 10.8: Procentilių metodu įvertintos PI ribos (punktyrinės linijos).

Visgi, statistikų skirstinys ne visada yra normalusis, o statistikos gali būti paslinktosios. Tad sprendžiant nemažą dalį statistikos uždavinių, koreguotasis procentilių metodas \(BC_a\) (angl. bias corrected and accelerated) (Efron 1987) laikomas vienu tiksliausių PI įvertinimui, nes atsižvelgia į netikslumus, kylančius dėl statistikos paslinktumo (angl. bias) ir skirstinio asimetrijos (acceleration). Tad šį metodą rekomenduočiau rinktis kaip pagrindinį. Visgi jo trūkumas yra tas, kad skaičiavimai gali trukti šiek tiek (ar net ženkliai) ilgiau nei taikant procentilių metodą.

10.4.3 Rekomenduojami informacijos šaltiniai

Daugiau teorinės medžiagos apie savirankos metodus galite rasti šiuose šaltiniuose:

1. „Bootstrap Methods and Permutation Tests“ (Hesterberg ir kt. 2017);
2. Savirankos būdu apskaičiuoti PI (Brightwell ir Dransfield 2013):
   1. principai ;
   2. kaip atlikti? (R programos kodai, demonstruojantys skaičiavimo principus);
   3. tinkamas ir netinkamas taikymas .

10.5.1 Metodų aprašymo gairės

Aprašant PI rezultatus pateikiamos abi intervalo ribos, pasikliovimo lygmuo, tiksliai nurodomas naudotas metodas bei kompiuterinė programa bei jos priedai, kuriais atlikti skaičiavimai, ir tikslios jų versijos. Įprastai (bet ne visada) pateikiamas taškinis įvertis. Metodikos dalyje galima nurodyti skaičiavimo formulę. Taip pat svarbu nurodyti informacijos šaltinį, kuris aprašo metodą (ypač proporcijų PI skaičiavimo atveju, nes galimų metodų yra daug). Įprastai rezultatai pateikiami arba tik grafiškai, arba tik tekste.

10.5.2 Rezultatų pateikimo pavyzdžiai

Aprašymas tekste rezultatų dalyje gali atrodyti taip:
„… ilgio vidurkis yra 3 cm (95% PI 2,54–3,46) …“ arba
„… 95% PI [2,54; 3,46] …“, arba (anglų kalba)
„… 95% CI [2.54, 3.46] …“.

Tik būtina paaiškinti, kad „PI“ yra pasikliautinasis intervalas (angl. CI – confidence interval). Pasikliautinuosius intervalus galima pateikti ir lentele ar grafiku.

Savirankos būdu skaičiuotų PI aprašymo pavyzdys.
Metodikos dalyje: „Pasikliautinieji intervalai skaičiuoti savirankos metodu sudarant 3000 replikacijų ir intervalų ribas įvertinant koreguotuoju procentilių metodu \(BC_a\) (Efron 1987). Skaičiavimams naudotas programos R (versija 4.3.3) paketas boot (versija 1.3.30).“
Rezultatų dalyje: „Tarp kintamųjų nustatyta vidutinio stiprumo koreliacija (Kendall \(\tau\) = 0,57 95% PI [0,52; 0,62]).“ Pastaba: apie koreliacinę analizę rašoma skyriuje „20 Koreliacinė analizė: ryšys tarp kintamųjų.“

10.5.3 PI braižymas

Pradėkime nuo to, kad statistinio grafiko paskirtis – tiksliai, aiškiai ir suprantamai perteikti informaciją.

Skaitinius (kiekybinius) kintamuosius apibendrinančias statistikas (vidurkį, medianą ir pan.) stulpeliais vaizduoti nėra korektiška, nes stulpeliai gali iškreipti duomenų suvokimą. Taip yra todėl, kad įprastai stulpeliai braižomi nuo grafiko apačios (dažnai nuo 0 ribos) iki vidurkio (ar kitos statistikos), o viršuje paliekama tuščia erdvė. Taip susidaro įspūdis, kad apatinė grafiko dalis yra svarbesnė, nes pats stulpelio buvimas ją per daug akcentuoja. Atkreipkite dėmesį į tai, kad pačioje apatinėje šios srities dalyje duomenų gali ir nebūti (pvz., pav. 10.9 A ir B: žemiau ribos lygios 100 gramų taškų apskritai nėra, bet stulpelio dalis ten atvaizduota). Tuo tarpu gali susidaryti įspūdis, kad srityje virš vidurkio duomenų nėra (pvz., pav. 10.9 grupės G-1 reikšmės viršija 400, tačiau grafike B ties 400 yra tuštuma). Tad šiuo atveju informacija perteikta nepakankamai tiksliai.

Efektyvesnis būdas – rezultatus atvaizduoti taškais (pav. 10.9 C). Tada perdėtų akcentų nesuteikiama nei sričiai virš, nei sričiai žemiau vidurkio.

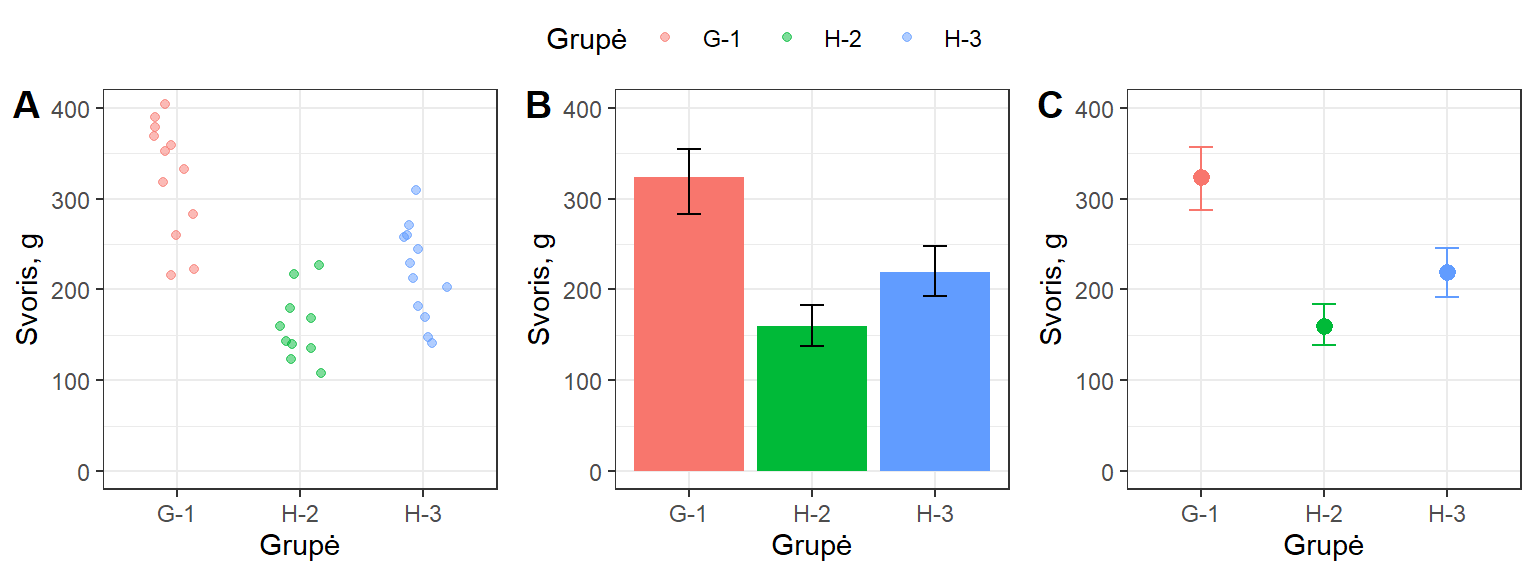
Pav. 10.9: Duomenys ir jų vidurkiai su pasikliautinaisiais intervalais (PI). A – Duomenys atvaizduoti taškais. B – Vidurkiai atvaizduoti stulpeliais (nerekomenduojama). C – Vidurkiai atvaizduoti taškais.

Proporcija apibūdina kategorinius (ar diskrečiuosius) kintamuosius. Tad šią aprašomąją statistiką vaizduoti stulpeliu yra prasminga ir korektiška (pav. 10.10).

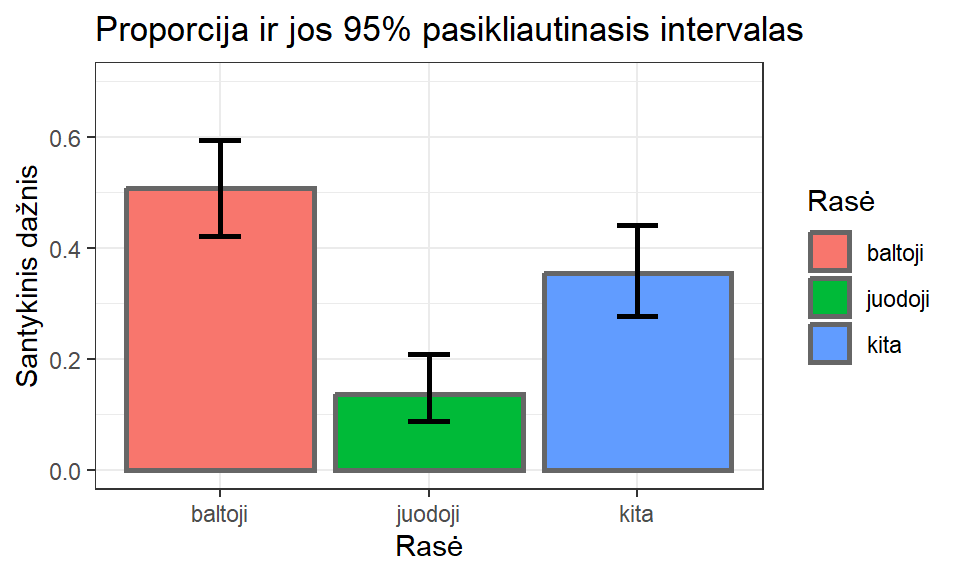
Pav. 10.10: Proporcijos ir jų pasikliautinieji intervalai.