17. Sklaidos lyginimas

Tikslas – susipažinti su statistinių hipotezių apie sklaidą (pvz., dispersijas) tikrinimo būdais ir išmokti patikrinti lygių dispersijų prielaidą.

Dispersija, standartinis nuokrypis (SD), MAD, IQR yra sklaidos matai. Hipotezėms tikrinti įprastai yra naudojama dispersija. Kriterijus, kuriuo siekiama patikrinti, ar skirtumai tarp dispersijų yra statistiškai reikšmingi, gali būti taikomas kaip:

  • pagrindinis kriterijus, pvz., jei norima įvertinti kokybę, pastovumą arba stabilumą, jei jie išreiškiami kaip sklaida (mažiau sklaidos → daugiau kokybės),
  • prielaidos apie lygias dispersijas (dar vadinama homoskedastiškumo arba dispersijų homogeniškumo prielaida) tikrinimo kriterijus (McDonald 2014j).

Situacija, kai kelių grupių dispersijos yra lygios, vadinama dispersijų homogeniškumu arba homoskedastiškumu.

Tikrinant prielaidas pradedantiesiems rekomenduoju Levene’o (skaitoma „Li-vỹ-no“) kriterijų su Brown-Forsythe (Brauno-Forsaito) pataisa (centras – mediana) (Brown ir Forsythe 1974), nes jis tinka ir normaliesiems, ir nuo normalumo nukrypusiems duomenims. Šis ir kai kurie kiti dispersijų (sklaidos) lyginimo kriterijai pateikti pav. 17.1 esančioje schemoje.

Vertinant skirtumus tarp dispersijų reikia kliautis ne tik statistiniais kriterijais, bet būtina atlikti ir aprašomąją statistiką: apskaičiuoti dispersijas, taip pat standartinius nuokrypius, IQR ir/arba MAD kiekvienai lyginamai grupei. Rekomenduojama pažiūrėti, kaip smarkiai skiriasi mažiausia ir didžiausia reikšmės. Pvz., ar skirtumas tarp dispersijų (ne tarp SD) mažesnis nei 3 kartai, ar didesnis. Taip pat svarbu nusibraižyti grafiką ir jame palyginti, sakykime, stačiakampės diagramos dėžučių plotį.

17.1 Pasirinkimų schema: sklaida

Statistiniai kriterijai dispersijoms (sklaidai) lyginti pateikti schemoje 17.1.

Schema yra supaprastinta ir tik rekomendacinio pobūdžio. Jos tikslas – būti „atspirties tašku“ renkantis analizės metodą. Konkrečiu atveju gali būti išlygų, papildomų sąlygų arba pasirinkimo variantų, kurie schemoje nepažymėti.

Schema, rekomenduojanti, kurį **dispersijų** lyginimo metodą pasirinkti. Įprastai prielaidų tikrinimui tinkamiausias yra Levene/Brown-Forsythe metodas, kai kiekvienos grupės centru laikoma mediana. Spalvinio žymėjimo reikšmės pateiktos skyriuje „\@ref(ht-schemos) [Schemos metodams pasirinkti](#ht-schemos)“.

Pav. 17.1: Schema, rekomenduojanti, kurį dispersijų lyginimo metodą pasirinkti. Įprastai prielaidų tikrinimui tinkamiausias yra Levene/Brown-Forsythe metodas, kai kiekvienos grupės centru laikoma mediana. Spalvinio žymėjimo reikšmės pateiktos skyriuje „12.4 Schemos metodams pasirinkti“.

Schemoje 17.1 skaičiais pažymėtų punktų paaiškinimai:

  • 1 \(\chi^2\) skaitoma „chi kvadratu“.
  • 2 Yra keli Livyno–Brauno-Forsaito kriterijaus variantai:
    1. Klasikinis Livyno kriterijus, kai duomenų centru laikomas vidurkis. Labiausiai tinka, kai duomenys yra daugmaž simetriški (NIST/SEMATECH 2012a).
    2. Brauno-Forsaito kriterijus (t.y., Livyno kriterijus su Browno-Forsaito pataisa), kai duomenų centru laikoma mediana. Tinka ir tada, kai duomenys yra asimetriški (NIST/SEMATECH 2012a). Tai pagrindinis kriterijaus variantas jį atliekant programa „R“.
      3 Literatūroje (pvz., (Čekanavičius ir Murauskas 2004, p.77)) ir statistinėse programose (pvz., „R“) dažnai vadinamas tiesiog Livyno kriterijumi, bet pažymint, kad centru laikytos medianos.

17.2 Statistinės hipotezės lyginant dispersijas

Kai naudojamas \(F\) kriterijus hipotezei apie dviejų grupių dispersijų lygybę tikrinti, statistinės hipotezės formuluojamos taip:

  • \(H_0\): dispersijos lygios, \(\sigma^2_1 = \sigma^2_2\) (skirtumo nėra);
  • \(H_1\):
    • arba dispersijos skiriasi, \(\sigma^2_1 \ne \sigma^2_2\) (dvipusė alternatyva),
    • arba \(\sigma^2_1 < \sigma^2_2\),
    • arba \(\sigma^2_1 > \sigma^2_2\) (vienpusės alternatyvos).

Jei naudojami kriterijai, kuriais tikrinama hipotezė apie kelių (2 ar daugiau) dispersijų lygybę, hipotezės:

  • \(H_0\): dispersijos lygios, \(\sigma^2_1 = \sigma^2_2 = ... = \sigma^2_n\) (skirtumo nėra);
  • \(H_1\): bent dviejų grupių (neaišku kurių) dispersijos skiriasi, \(\sigma^2_i \ne \sigma^2_j\) (dvipusė alternatyva).

Kriterijus lygina iš karto visų grupių dispersijas, todėl gaunama viena \(p\) reikšmė.

Jei reikšmingumo lygmuo \(\alpha = 0{,}05\), tai, kai:

  • \(p\ge 0{,}05\), teigiame, kad skirtumas tarp dispersijų yra statistiškai nereikšmingas (neatmetame \(H_0\));
  • \(p< 0{,}05\), teigiame, kad skirtumas tarp dispersijų yra statistiškai reikšmingas (priimame \(H_1\)).

Įprastai, kai \(p \ge 0{,}05\), laikoma, kad lygių dispersijų prielaida tenkinama (nes skirtumai tarp dispersijų nėra statistiškai reikšmingi).

17.3 Statistiniai kriterijai

17.3.1 \(\chi^2\) kriterijus vienos imties dispersijai lyginti su reikšme

Yra \(\chi^2\) (chi-kvadratu) kriterijaus variantas, skirtas vienos imties dispersijos lyginimui su konkrečia reikšme. Tinka, jei duomenys griežtai normalieji ir imtis pakankamo dydžio (įprastai taikant \(\chi^2\) kriterijus reikia, kad imties dydis būtų bent 30). Apie jį plačiau rašoma (NIST/SEMATECH 2012c).

Rezultatų pavyzdys

Rezultatų pavyzdys kriterijų taikant programa „R“:

    One Sample Chi-Square test on variance

data:  y
X-squared = 0.12333, df = 5, p-value = 0.0005439
alternative hypothesis: true variance is not equal to 2.5
95 percent confidence interval:
 0.02402753 0.37094445
sample estimates:
variance of x 
   0.06166667

Tarp kompiuterinės programos rezultatų turėtumėte pamatyti:

  • metodo pavadinimą (One Sample Chi-Square test on variance),
  • \(\chi^2\) statistikos reikšmę (X-squared = 0.12333),
  • \(\chi^2\) skirstinio parametrų reikšmes (df = 5),
  • \(p\) reikšmę (p-value = 0.0005439),
  • alternatyvos rūšį (is not equal to, t.y., dvipusė alternatyva).

Taip pat tarp rezultatų pateikta dispersijos reikšmė (0.06166667) ir jos pasikliautinasis intervalas (95 percent confidence interval:, 0.02402753 0.37094445).

17.3.2 F kriterijus dviejų imčių dispersijoms lyginti

\(F\) kriterijus skirtas lygiai dviejų imčių dispersijoms lyginti, jei duomenys griežtai normalieji ir kiekviena imtis pakankamo dydžio. Jei duomenys ne normalieji, kriterijus labiau vertins nuokrypį nuo normalumo nei skirtumą tarp dispersijų. Apie kriterijų plačiau rašo (NIST/SEMATECH 2012d).

Rezultatų pavyzdys

Rezultatų pavyzdys kriterijų taikant programa „R“:

    F test to compare two variances

data:  y by grupe
F = 2.7143, num df = 2, denom df = 2, p-value = 0.5385
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
   0.06959707 105.85714286
sample estimates:
ratio of variances 
          2.714286

Tarp kompiuterinės programos rezultatų turėtumėte pamatyti:

  • metodo pavadinimą (F test to compare two variances),
  • \(F\) statistikos reikšmę (F = 2.7143),
  • \(F\) skirstinio parametrų reikšmes (num df = 2, denom df = 2),
  • \(p\) reikšmę (p-value = 0.5385),
  • alternatyvos rūšį (is not equal to, t.y., dvipusė alternatyva).

Taip pat tarp rezultatų pateiktas dviejų grupių dispersijų santykis (2.714286) ir jo pasikliautinasis intervalas (95 percent confidence interval:, 0.06959707 105.85714286). Pastaba: skirtumo nėra, kai santykis lygus 1.

17.3.3 Bartlett kriterijus kelių imčių dispersijoms lyginti

Bartleto (Bartlett) kriterijus skirtas kelių imčių dispersijų lyginimui, jei duomenys griežtai normalieji ir kiekviena imtis pakankamo dydžio. Jei duomenys ne normalieji, kriterijus labiau vertins nuokrypį nuo normalumo nei skirtumą tarp dispersijų. Apie kriterijų plačiau rašo (NIST/SEMATECH 2012b), (Čekanavičius ir Murauskas 2004, p.75), (Venclovienė 2010, p.244).

Rezultatų pavyzdys

Rezultatų pavyzdys kriterijų taikant programa „R“:

    Bartlett test of homogeneity of variances

data:  y by grupe
Bartlett's K-squared = 0.38328, df = 1, p-value = 0.5359

Tarp kompiuterinės programos rezultatų turėtumėte pamatyti:

  • metodo pavadinimą (Bartlett test of homogeneity of variances),
  • \(K^2\) statistikos reikšmę (K-squared = 0.38328),
  • \(\chi^2\) skirstinio parametrų reikšmes (df = 1),
  • \(p\) reikšmę (p-value = 0.5359).

17.3.4 Levene ir Brown-Forsythe kriterijai kelių imčių dispersijoms lyginti

Livyno (Levene) – Brauno-Forsaito (Brown-Forsythe) kriterijai tinka ir tada, kai duomenys yra šiek tiek nukrypę nuo normalumo. Kai centras – vidurkis, kriterijus turėtų vadintis Levene’o (Levene 1960), kitais atvejais – Brown-Forsythe (Brown ir Forsythe 1974) vardu. Plačiau apie šiuos kriterijus rašo (NIST/SEMATECH 2012a), (Čekanavičius ir Murauskas 2004, p.76), (Venclovienė 2010, p.245).

Rezultatų pavyzdys

Šio kriterijaus, taikyto programa „R“, rezultatų pavyzdys pateiktas pav. 17.2.

Levene ir Brown-Forsythe kriterijų rezultatai.

Pav. 17.2: Levene ir Brown-Forsythe kriterijų rezultatai.

Kriterijus yra pagrįstas tikimybių iš \(F\) skirstinio skaičiavimu, tad kaip pagal rezultatų lentelę gauti \(p\) reikšmę, rodoma pav. 17.3.

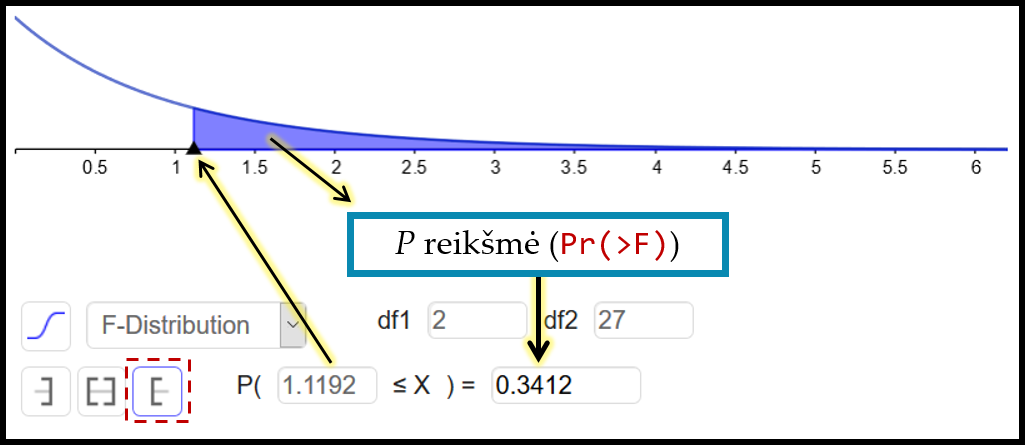
Levene / Brown-Forsythe kriterijaus $p$ reikšmės skaičiavimas programos „Geogebra“ tikimybių skaičiuokle. Visais atvejais imama tikimybė „daugiau už“. Rezultatai tie patys, kaip pav. \@ref(fig:09-Levene-test-result).

Pav. 17.3: Levene / Brown-Forsythe kriterijaus \(p\) reikšmės skaičiavimas programos „Geogebra“ tikimybių skaičiuokle. Visais atvejais imama tikimybė „daugiau už“. Rezultatai tie patys, kaip pav. 17.2.

Levene’o / Brown-Forsythe kriterijaus rezultatų lentelėje labiausiai mus dominantis dalykas yra \(p\) reikšmė. Ji pateikta stulpelyje Pr(>F) ir yra lygi 0,34 (suapvalinta). Šis rezultatas rodo, kad skirtumas tarp dispersijų nėra statistiškai reikšmingas (lygių dispersijų prielaida tenkinama).

Galima Levene ir Brown-Forsythe kriterijų rezultatų pateikimo forma.

Pav. 17.4: Galima Levene ir Brown-Forsythe kriterijų rezultatų pateikimo forma.

Dar keli pavyzdžiai:

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1     0.4 0.5614
       4      
Levene's Test for Homogeneity of Variance (center = "mean")
      Df F value Pr(>F)
group  1  0.6429 0.4676
       4

Tarp kompiuterinės programos rezultatų turėtumėte pamatyti:

  • metodo pavadinimą (Levene's Test for Homogeneity of Variance (center = "mean")),
  • \(F\) statistikos reikšmę (F value = 0.6429 arba statistic),
  • \(F\) skirstinio parametrų reikšmes (Df, 1 (skaitiklio laisvės laipsniai, l.l.) ir 4 (vardiklio l.l.) arba df1 ir df2),
  • \(p\) reikšmę (Pr(>F) = 0.4676 arba p, arba p-value).

17.4 Rezultatų aprašymas: sklaida

Jei kriterijus taikomas kaip pagrindinis analizės metodas, aprašydami rezultatus laikykitės skyriuje „11.7 Rezultatų aprašymo principai“ išdėstytų principų. Pvz., „…skirtumas tarp dispersijų buvo statistiškai nereikšmingas (Brown-Forsythe kriterijus, \(F(2; ~27) = 1{,}12, ~ p = 0{,}341\)).“ Taip pat reikia nurodyti kiekvienos grupės dispersijas arba standartinius nuokrypius. Jei grupių daug, šie rezultatai pateikiami lentele. Rekomenduojama pateikti grafiką, kuriame būtų lyginamos grupių dispersijos (sklaida).

Jei kriterijus taikomas kaip prielaidų tikrinimo metodas, įprastai užtenka teigti, kad, pvz., „lygių dispersijų prielaida tikrinta Brown-Forsythe kriterijumi“ bei „dispersijų homogeniškumo prielaida buvo tenkinama“ arba „visos modeliui keliamos prielaidos buvo tenkinamos“, arba „lygių dispersijų prielaida buvo pažeista, todėl… (darėme tą ir aną)“.

Informacijos šaltiniai

Brown M.B., Forsythe A.B. Robust Tests for the Equality of Variances, Journal of the American Statistical Association 69(346): 364–367 (1974). DOI: 10.1080/01621459.1974.10482955.
Čekanavičius V., Murauskas G. Statistika ir jos taikymai II. Vilnius: TEV (2004).
Levene H. Robust tests for equality of variances. Olkin I. ir kt., sud. Contributions to Probabilityand Statistics: Essays in Honor of Harold Hotelling. Menlo Park, CA: StanfordUniversity Press. (1960).
McDonald J.H. Homoscedasticity and heteroscedasticity. Handbook of Biological Statistics. Baltimore, Maryland: Sparky House Publishing. (2014j). Prieiga per internetą: http://www.biostathandbook.com/homoscedasticity.html.
NIST/SEMATECH 1.3.5.10. Levene Test for Equality of Variances. e-Handbook of Statistical Methods (Engineering Statistics Handbook). (2012a). Prieiga per internetą: https://www.itl.nist.gov/div898/handbook/eda/section3/eda35a.htm.
NIST/SEMATECH 1.3.5.7. Bartlett’s Test. e-Handbook of Statistical Methods (Engineering Statistics Handbook). (2012b). Prieiga per internetą: https://www.itl.nist.gov/div898/handbook/eda/section3/eda357.htm.
NIST/SEMATECH 1.3.5.8. Chi-Square Test for the Variance. e-Handbook of Statistical Methods (Engineering Statistics Handbook). (2012c). Prieiga per internetą: https://www.itl.nist.gov/div898/handbook/eda/section3/eda358.htm.
NIST/SEMATECH 1.3.5.9. F-Test for Equality of Two Variances. e-Handbook of Statistical Methods (Engineering Statistics Handbook). (2012d). Prieiga per internetą: https://www.itl.nist.gov/div898/handbook/eda/section3/eda359.htm.
Venclovienė J. Statistiniai metodai medicinoje. Kaunas: Vytauto didžiojo universitetas (2010). Prieiga per internetą: https://www.vdu.lt/cris/bitstream/20.500.12259/271/1/ISBN9789955125587.pdf.