16. Normalumo tikrinimas

Tikslas – išmokti patikrinti vienmačio normalumo (normaliojo pasiskirstymo) prielaidą.

16.1 Pasiskirstymo normalumas

Normalumu statistikoje vadinama situacija, kai duomenys yra pasiskirstę pagal normalųjį (Gauso) skirstinį. Normalumo prielaida – tai reikalavimas, kad duomenys skirstytųsi (daugmaž) normaliai. Daugelis klasikinės statistikos metodų, vadinamų parametriniais, sukurti grindžiant šia prielaida. Tad prieš taikant tokius kriterijus, reikia įsitikinti, kad reikalavimas yra tenkinamas, nes kitu atveju smarkiai padidėja I rūšies klaidos (klaidingų atradimų) tikimybė (McDonald 2014k). Statistiniai normalumo tikrinimo kriterijai padeda įvertinti, ar duomenų pasiskirstymo nukrypimas nuo normaliojo yra statistiškai reikšmingas, grafiniai būdai – nustatyti nuokrypio pobūdį ir dydį. Normalumas gali būti vienmatis (pav. 16.1) – skaičiuojamas pagal vieną kiekybinį kintamąjį (to mums beveik visada ir reikia šio kurso metu) ar daugiamatis (pav. 16.2) – skaičiuojamas pagal kelis kiekybinius kintamuosius (pvz., tiesinė koreliacinė analizė reikalauja, kad būtų tenkinama dvimačio normalumo prielaida).

„Normalieji duomenys“ = „pagal normalųjį skirstinį pasiskirstę duomenys.“

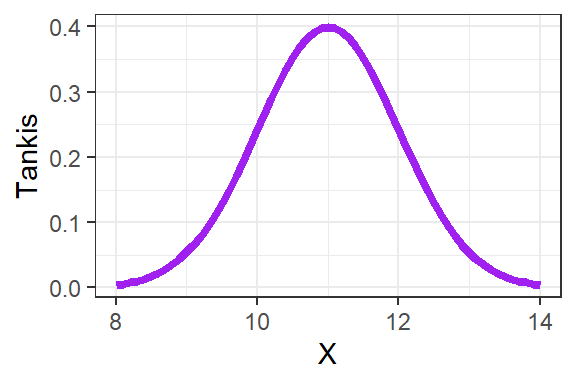
Pav. 16.1: Vienmačio normaliojo skirstinio pavyzdys (tankio funkcija).

Pav. 16.2: Dvimačio normaliojo skirstinio pavyzdys (interaktyvus grafikas). Vaizduojama tankio funkcija.

Toliau šiame skyriuje kalbėsime tik apie vienmatį normalumą.

16.2 Pasirinkimų schema: normalumas

Normalumo prielaidai tikrinti yra keletas būdų, kurių pavyzdžiai pateikti pav. 16.3. Rekomenduoju geriausiai įsiminti kvantilių palyginimo (QQ) diagramą ir Shapiro-Wilk kriterijų, kuriuos šio kurso metu naudosime dažniausiai.

Schema yra supaprastinta ir tik rekomendacinio pobūdžio. Jos tikslas – būti „atspirties tašku“ renkantis analizės metodą. Konkrečiu atveju gali būti išlygų, papildomų sąlygų arba pasirinkimo variantų, kurie schemoje nepažymėti.

$Metodai vienmačio pasiskirstymo **normalumui** tikrinti. Spalvinio žymėjimo reikšmės pateiktos skyriuje „\@ref(ht-schemos) [Schemos metodams pasirinkti](#ht-schemos)“.$

Pav. 16.3: Metodai vienmačio pasiskirstymo normalumui tikrinti. Spalvinio žymėjimo reikšmės pateiktos skyriuje „12.4 Schemos metodams pasirinkti“.

Schemoje 16.3 skaičiais pažymėtų punktų paaiškinimai:
¹ Šis apribojimas galioja kriterijų taikant programa „R“. Apskritai, jei imtis per maža (pvz., $n_i < 20$), kriterijus gali klaidingai rodyti, kad normalumo prielaida tenkinama (nors iš tiesų trūksta duomenų statistiniam reikšmingumui pasiekti).
² Pvz., histogramos ir teorinės normaliosios kreivės palyginimas.

Įprastai duomenų normalumą reikia tikrinti kiekvienam tiriamam pogrupiui atskirai, o ne visiems turimiems duomenims iš karto.

Normalumo prielaida yra tenkinama tik tada, jei padarome išvadą, kad kiekvienos grupės pasiskirstymas yra daugmaž normalusis.

„Normaliojo vakarėlio“ taisyklė: vakarėlis normalus tik tada, jei visi jame dalyvaujantys yra normalūs.

16.3 Statistiniai kriterijai normalumui tikrinti

Yra keletas kriterijų (angl. statistical tests) vienmačio pasiskirstymo normalumui tikrinti: Shapiro-Wilk’o (Shapiro ir Wilk 1965), Anderson-Darling, Kolmogorovo-Smirnovo su Lilliefor’o pataisa ir kiti. Tikrinant prielaidą reikia pasirinkti tik vieną, kuris, jūsų nuomone, labiausiai tinka. Taikant šiuos kriterijus, statistinės hipotezės formuluojamos taip:

$H_0$: pasiskirstymas yra normalusis, $X \sim \mathcal{N}(\mu, ~\sigma^2)$ (nuokrypio nuo normalumo nėra);
$H_1$: pasiskirstymas nėra normalusis, $X \not\sim \mathcal{N}(\mu, ~\sigma^2)$ (nuokrypis nuo normalumo yra).

Kiekvienas iš statistinių kriterijų naudoja skirtingą nuokrypio nuo normalumo matą (kriterijaus statistiką), pagal kurį skaičiuojama $p$ reikšmė. Ši, negriežtai kalbant, parodo, kokia tikimybė gauti mūsų tyrime apskaičiuotą nuokrypį nuo normalumo arba dar didesnį, jei iš tiesų pasiskirstymas yra normalusis. Įprastai reikšmingumo lygmuo (tikimybė $\alpha$) – riba, kurią pasirenkame sprendimui priimti – yra lygi $\alpha = \frac{1}{20} = 0{,}05$. Tokiu atveju (kai $\alpha = 0{,}05$):

jei $p \ge 0{,}05$, tada neturime pagrindo atmesti $H_0$: duomenų pasiskirstymo nuokrypis nuo normaliojo yra statistiškai nereikšmingas ir normalumo prielaida tenkinama;
jei $p < 0{,}05$, duomenų pasiskirstymo nuokrypis nuo normaliojo yra statistiškai reikšmingas ir normalumo prielaida pažeidžiama.

Jei jūsų naudojama kompiuterinė programa skaičiuoja ir koreguotąsias reikšmės (p adjusted), tai prielaida tikrinama pagal įprastines (nekoreguotąsias) $p$.

Hipotezė apie skirstinių normalumą tikrinama kiekvienai grupei atskirai, tad gaunama tiek $p$ reikšmių, kiek yra lyginamų grupių.

16.3.1 Normalumo tikrinimas ir imties dydis

Prisiminkite, kad mažoms imtims (tarkime, kai n < 20) kriterijui gali nepakakti statistinės galios atmesti nulinę hipotezę, todėl tokioje situacijoje dažnai gausime klaidinantį rezultatą, kad nuokrypiai nuo normalumo yra nereikšmingi. Tad iš mažų imčių darytomis išvadomis (jei tokiomis išvadomis apskritai galima tikėti), kad normalumo prielaida tenkinama, neturėtume tikėti, bet turėtume atkreipti dėmesį, jei rezultatas statistiškai reikšmingas (Field 2016, p.413).

Didelėms imtims naudojant statistinius kriterijus net maži nuokrypiai bus pripažįstami statistiškai reikšmingais. Iš centrinės ribinės teoremos (CRT) žinome, kad vidurkių skirstinys smarkiai supanašėja su normaliuoju, kai imtis didelė. Tad kai kurie autoriai (Field 2016, p.413) tokioms imtims normalumo kriterijų siūlo visai nenaudoti ir dėl normalumo prielaidos apskritai nesijaudinti. Kiti (Clapham 2016; McDonald 2014k), jei normalumas tikrinamas kaip $t$ kriterijaus ar dispersinės analizės prielaida (šios analizės nėra labai jautrios nedideliems normalumo prielaidos pažeidimams, jei imtys didelės), siūlo naudoti grafinius būdus, nes normalumo kriterijus gali būti per jautrus nukrypimams nuo normalumo. Normalumui tikrinti skirti grafikai (QQ diagrama, histograma ar kiti) parodo nuokrypio nuo normalumo pobūdį ir stiprumą. Taip pat yra siūlymų didelių imčių atveju naudoti mažesnį reikšmingumo lygmenį, pvz., $0{,}001$.

Apibendrinti galima McDonald (2014k) mintimi laikytis taisyklių, kurios yra nusistovėjusios jūsų tyrimų srityje, ir daryti taip, kaip daro daugelis šios srities tyrėjų.

16.3.2 Resursai

Rekomenduojami resursai apie normalumo tikrinimą apskritai:

„Normality“ (McDonald 2014k).

Resursai apie Shapiro-Wilk kriterijų:

Resursai apie Lilliefor’o / Kolmogorovo-Smirnovo kriterijų:

„10: Kolmogorov-Smirnov test“

16.4 Grafiniai būdai normalumui tikrinti

Vienmačio (t.y., įvertinamo pagal vieną kintamąjį) normalumo prielaidą ar jos pažeidimus preliminariai galime įvertinti pagal vienmačio pasiskirstymo grafikus – histogramą, branduolių tankio grafiką ar net stačiakampės diagramos, jei nukrypimai labai ryškūs. Kartu su šiais grafikais rekomenduojama nusibrėžti ir specializuotus, tokius kaip kvantilių palyginimo diagrama (pav. 16.6, 16.7).

16.4.1 Kvantilių palyginimo (QQ) diagrama

Kvantilių palyginimo, arba kvantilių-kvantilių (QQ), diagrama (angl. quantile-quantile plot, QQ plot) (Wilk ir Gnanadesikan 1968) yra grafinis būdas, skirtas palyginti skirstinių atitikimą. Dažnai juo lyginama, ar empirinių – ypač tolydžiųjų – duomenų pasiskirstymas atitinka teoriniu modeliu (pvz., normaliuoju) aprašomą pasiskirstymą. Iš šio apibūdinimo aišku, kad QQ diagrama gali būti naudojama ne tik normalumui tikrinti. Visgi aptarkime, kaip naudojama būtent šiuo tikslu.

QQ diagramos x ašyje įprastai atidedami teorinio modelio kvantiliai, o y ašyje – empirinių duomenų kvantiliai (kai kuriose programose x ir y ašys gali būti sukeistos vietomis). X ašyje gali būti tiek labiausiai jūsų duomenis atitinkančio normaliojo skirstinio (pav. 16.4), tiek ir standartinio normaliojo (pav. 16.5) skirstinio kvantiliai. Visais atvejais, kuo QQ diagramos taškų išsidėstymas panašesnis į tiesę, einančią ties grafiko įstrižaine, tuo duomenys geriau atitinka modelį. Ypač svarbu, kad vienoje tiesėje būtų duomenų taškai, esantys tarp pirmojo $(Q_1)$ ir trečiojo $(Q_3)$ kvartilių. Visi kiti orientyrai (papildoma atskaitos tiesė ir jos pasikliautinieji intervalai, kaip pav. 16.5) yra tik pagalbiniai dalykai.

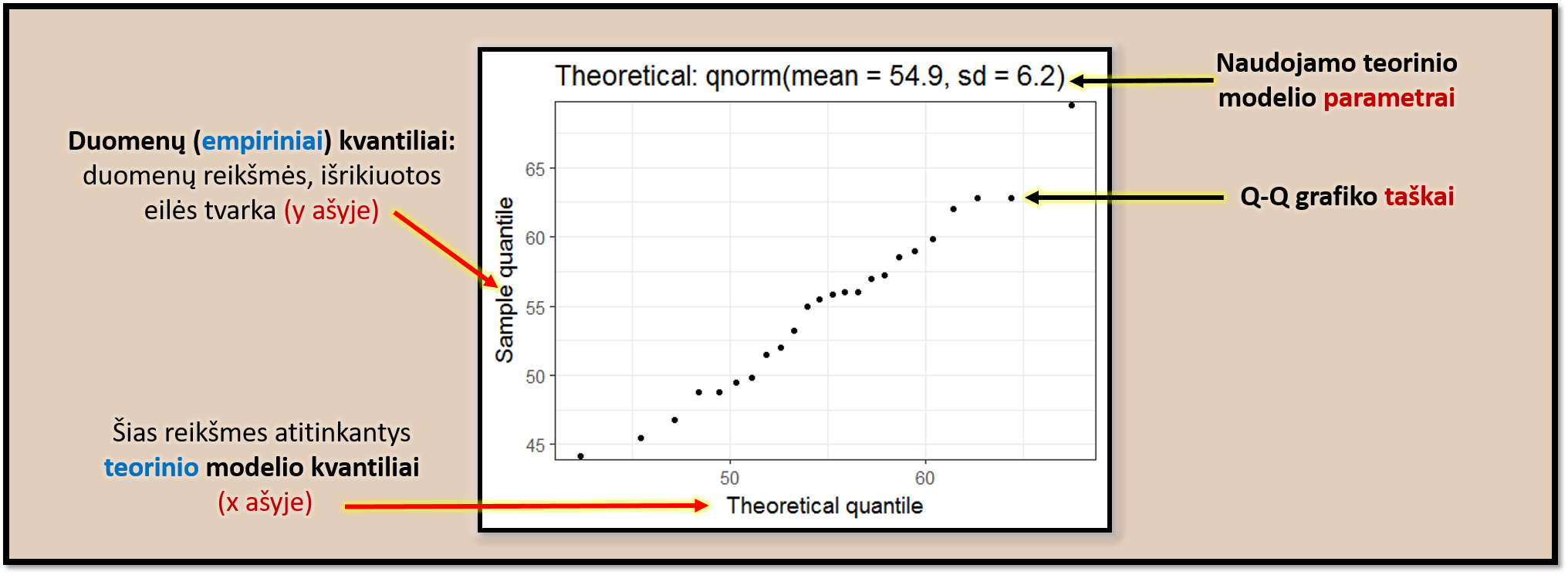
Pav. 16.4: Įprasta kvantilių-kvantilių (QQ) diagrama.

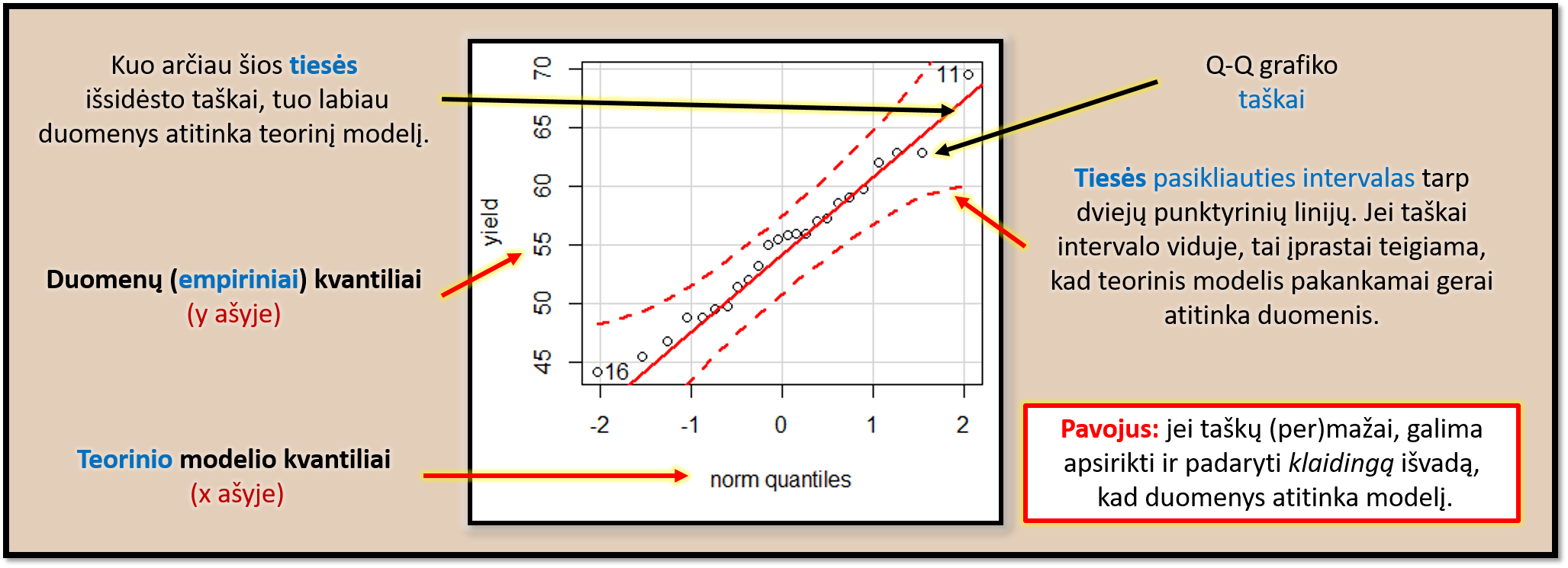
Pav. 16.5: Kvantilių-kvantilių (QQ) diagrama su atskaitos tiese ir šios tiesės pasikliautinuoju intervalu.

Kuo labiau pasiskirstymas skiriasi nuo teorinio, tuo labiau taškai nukrypsta nuo išsidėstymo vienoje tiesėje ties įstrižaine. Keletas pavyzdžių, kaip atrodo skirstinį atitinkantys ir aiškiai jo neatitinkantys duomenys, vaizduojama pav. 16.6 ir 16.7. Kai kurių grupių QQ grafikai padidintai rodomi pav. 16.8. O pav. 16.9 iliustruoja problemą, jei taškų yra labai mažai.

Jei reikia įvertini, ar QQ diagramoje matomi nuokrypiai yra statistiškai reikšmingi, galite naudoti Shapiro-Wilk normalumo kriterijų.

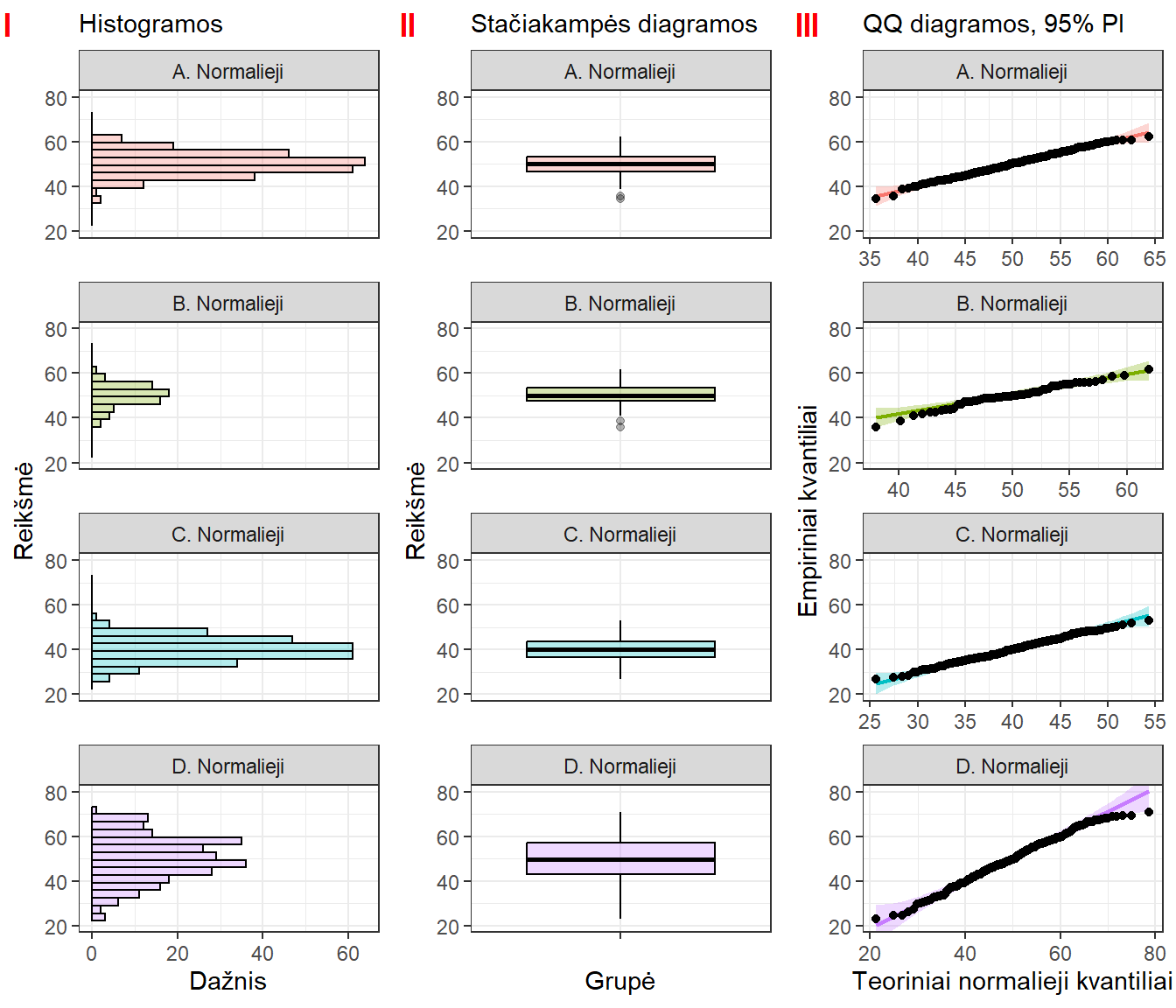
$Normalieji duomenys atvaizduoti skirtingais būdais: histogramomis (I), stačiakampėmis diagramomis (II) ir QQ (kvantilių palyginimo) diagramomis, kurios empirinį skirstinį lygina su normaliuoju (III). Jei duomenys daugmaž normalieji, taškai išsidėsto daugmaž į vieną tiesę ties grafiko įstrižaine. Nuokrypis nuo šios kreivės rodo nuokrypį nuo normalumo. Duomenys tie patys, kaip ir \@ref(fig:plot-c1-2) bei \@ref(fig:plot-c5-6-7-8) paveiksluose: **A** -- lyginamoji grupė, **B** -- imties dydis mažesnis, **C** -- mažesnis vidurkis, **D** -- sklaida didesnė. QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.$

Pav. 16.6: Normalieji duomenys atvaizduoti skirtingais būdais: histogramomis (I), stačiakampėmis diagramomis (II) ir QQ (kvantilių palyginimo) diagramomis, kurios empirinį skirstinį lygina su normaliuoju (III). Jei duomenys daugmaž normalieji, taškai išsidėsto daugmaž į vieną tiesę ties grafiko įstrižaine. Nuokrypis nuo šios kreivės rodo nuokrypį nuo normalumo. Duomenys tie patys, kaip ir 5.8 bei 5.11 paveiksluose: A – lyginamoji grupė, B – imties dydis mažesnis, C – mažesnis vidurkis, D – sklaida didesnė. QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.

$Ne normalieji ir turintys išskirčių duomenys atvaizduoti skirtingais būdais: histogramomis (I), stačiakampėmis diagramomis (II) ir QQ (kvantilių palyginimo) diagramomis, kurios empirinį skirstinį lygina su normaliuoju (III). Jei duomenys daugmaž normalieji, taškai išsidėsto daugmaž į vieną tiesę ties grafiko įstrižaine. Nuokrypis nuo šios kreivės rodo nuokrypį nuo normalumo. Duomenys tie patys, kaip ir \@ref(fig:plot-c1-2) bei \@ref(fig:plot-c5-6-7-8) paveiksluose: **E** -- dvi viršūnės, **F** -- dešinioji asimetrija, **G** -- kairioji asimetrija, **H** -- dvi galimos išskirtys. QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.$

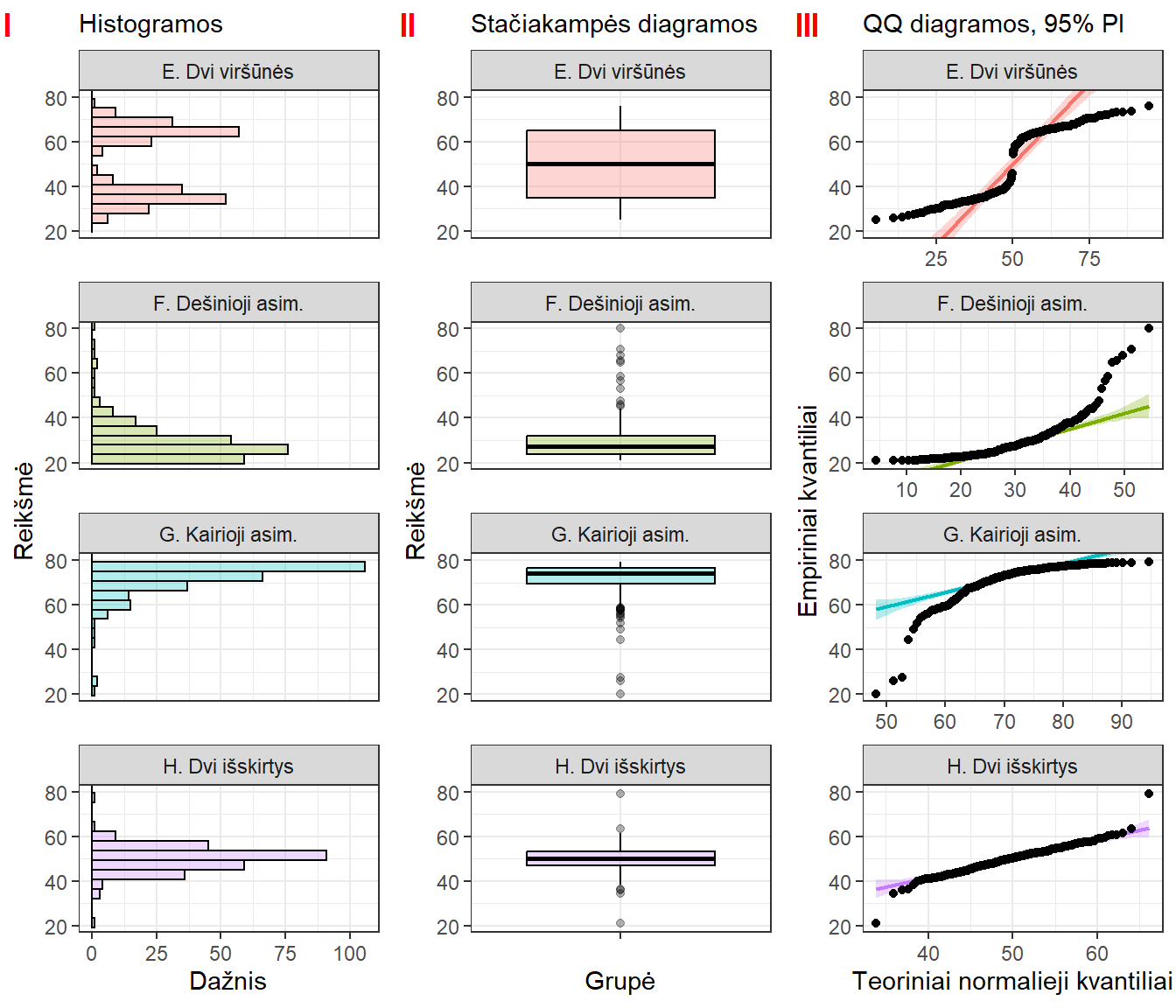
Pav. 16.7: Ne normalieji ir turintys išskirčių duomenys atvaizduoti skirtingais būdais: histogramomis (I), stačiakampėmis diagramomis (II) ir QQ (kvantilių palyginimo) diagramomis, kurios empirinį skirstinį lygina su normaliuoju (III). Jei duomenys daugmaž normalieji, taškai išsidėsto daugmaž į vieną tiesę ties grafiko įstrižaine. Nuokrypis nuo šios kreivės rodo nuokrypį nuo normalumo. Duomenys tie patys, kaip ir 5.8 bei 5.11 paveiksluose: E – dvi viršūnės, F – dešinioji asimetrija, G – kairioji asimetrija, H – dvi galimos išskirtys. QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.

$Padidintos QQ diagramos. Duomenys tie patys, kaip ir \@ref(fig:plot-c1-2), \@ref(fig:plot-c5-6-7-8), \@ref(fig:07-qq-4a), \@ref(fig:07-qq-4b) paveiksluose: **B** -- normalieji duomenys, **F** -- dešinioji asimetrija, **G** -- kairioji asimetrija, **H** -- dvi galimos išskirtys. QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.$

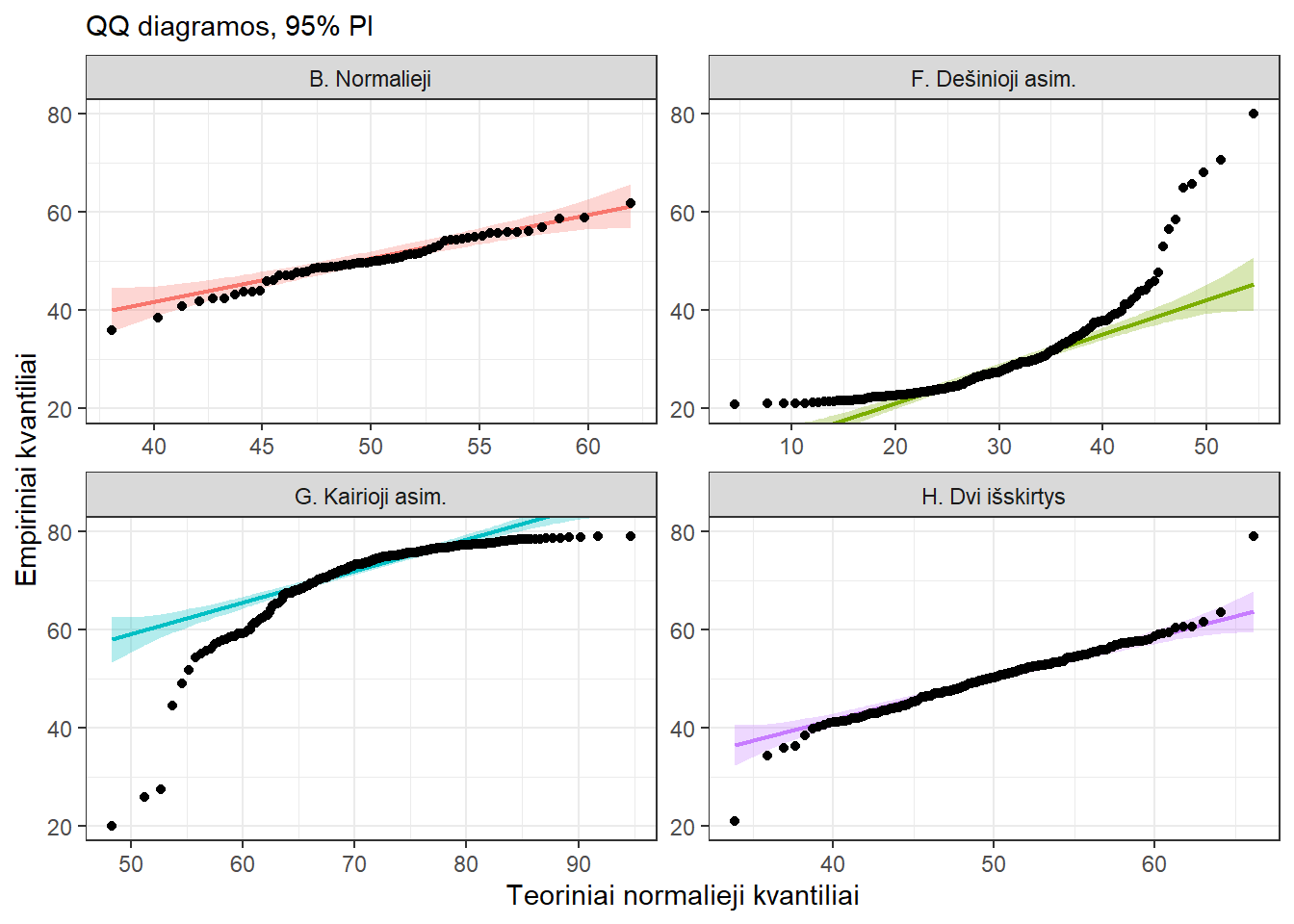
Pav. 16.8: Padidintos QQ diagramos. Duomenys tie patys, kaip ir 5.8, 5.11, 16.6, 16.7 paveiksluose: B – normalieji duomenys, F – dešinioji asimetrija, G – kairioji asimetrija, H – dvi galimos išskirtys.
QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.

$QQ diagramos, **kai imtys mažos**: pav. \@ref(fig:07-qq-4c) vaizduojamų duomenų poaibis (grupėje po 10 narių). Kai imties dydžiai maži, sunku vertinti nuokrypius nuo normalumo. QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.$

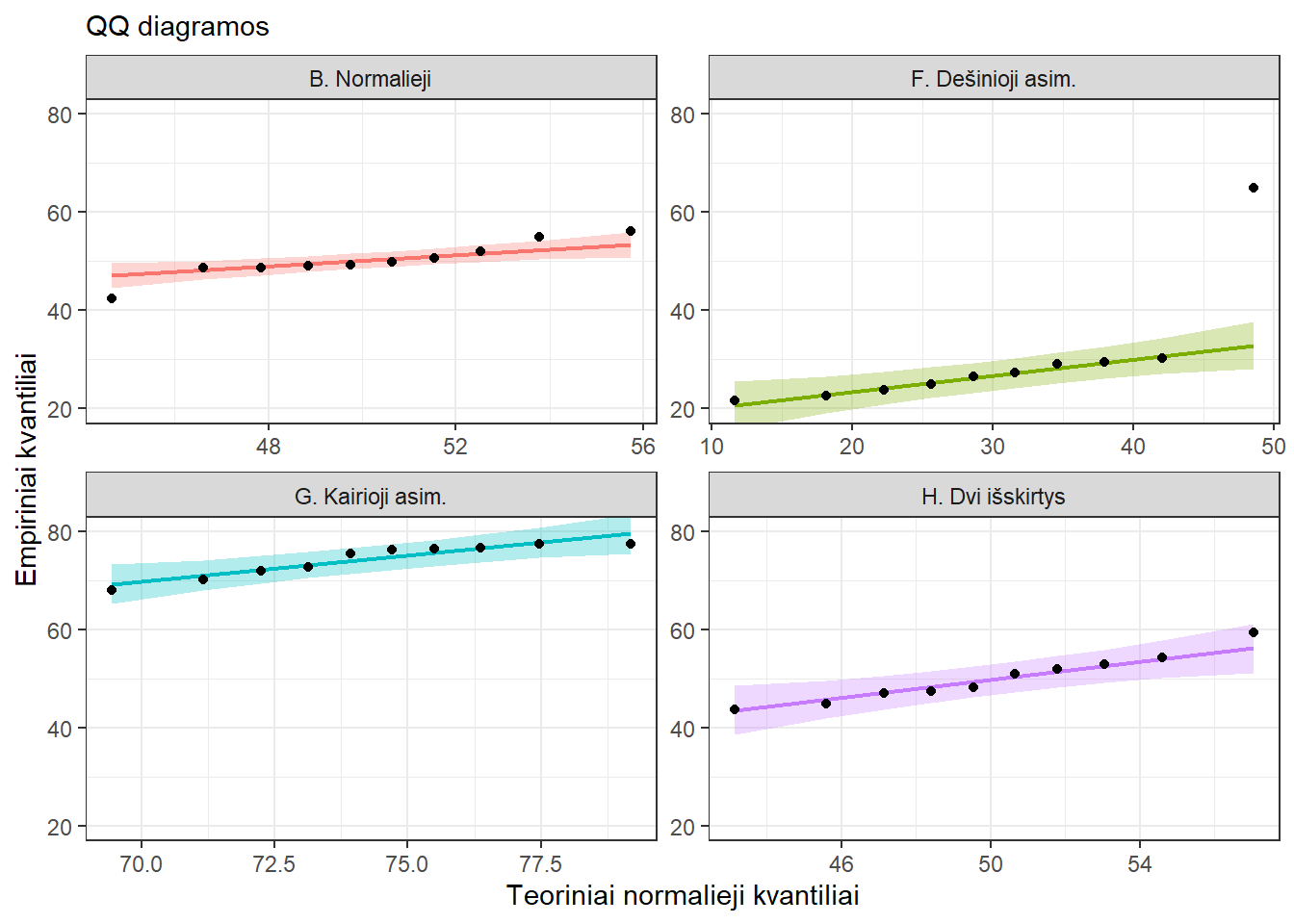
Pav. 16.9: QQ diagramos, kai imtys mažos: pav. 16.8 vaizduojamų duomenų poaibis (grupėje po 10 narių). Kai imties dydžiai maži, sunku vertinti nuokrypius nuo normalumo. QQ diagramos vaizduojamos su pagalbine linija ir 95% jos pasikliautinuoju intervalu.

O štai vienas iš galimų algoritmų, kaip braižoma QQ diagrama:

Sudaroma duomenų variacinė eilutė (reikšmių išdėstymas nuo mažiausios iki didžiausios);
Kiekvienai reikšmei priskiriama kvantilio eilė (skaičius nuo 0 iki 1):
- Pvz., taškas, variacinę eilutę dalijantis į 2 lygias dalis yra mediana, tad jo eilė yra 0,5.
- Pirmojo ir trečiojo kvartilių (Q1 ir Q3) eilė yra atitinkamai 0,25 ir 0,75.
Pagal iš duomenų įvertintus skirstinio parametrus, parenkamas konkretus skirstinys:
- pvz., jei norime tikrinti normalumą, iš duomenų įvertiname vidurkį ir dispersiją (normaliojo skirstinio parametrus $\mu$ ir $\sigma^2$).
Naudodami sudarytą skirstinio lygtį ir duomenų taškų kvantilių eilę, apskaičiuojame teorinius kvantilius.
X ašyje atidedame teorinius kvantilius, Y ašyje – empirinius. Tai ir yra QQ diagrama.
Papildomai galime atidėti pagalbinę tiesę ir tam yra keletas būdų. Vienas jų:
- nubrėžti tiesę per Q1 ir Q3 atitinkančius taškus.

Papildomi resursai:

Apie kvantilių skaičiavimą „StatQuest: Quantiles and Percentiles, Clearly Explained!!!“ .
Apie QQ diagramos sudarymą „StatQuest: Quantile-Quantile Plots (QQ plots), Clearly Explained“ .

16.4.2 Tikimybių palyginimo (PP) diagrama

Tikimybių palyginimo (tikimybių-tikimybių, PP) diagrama interpretuojama analogiškai, kaip ir QQ diagrama. Tik joje atidedami ne kvantiliai, o teorinės ir empirinės tikimybės (pav. 16.10).

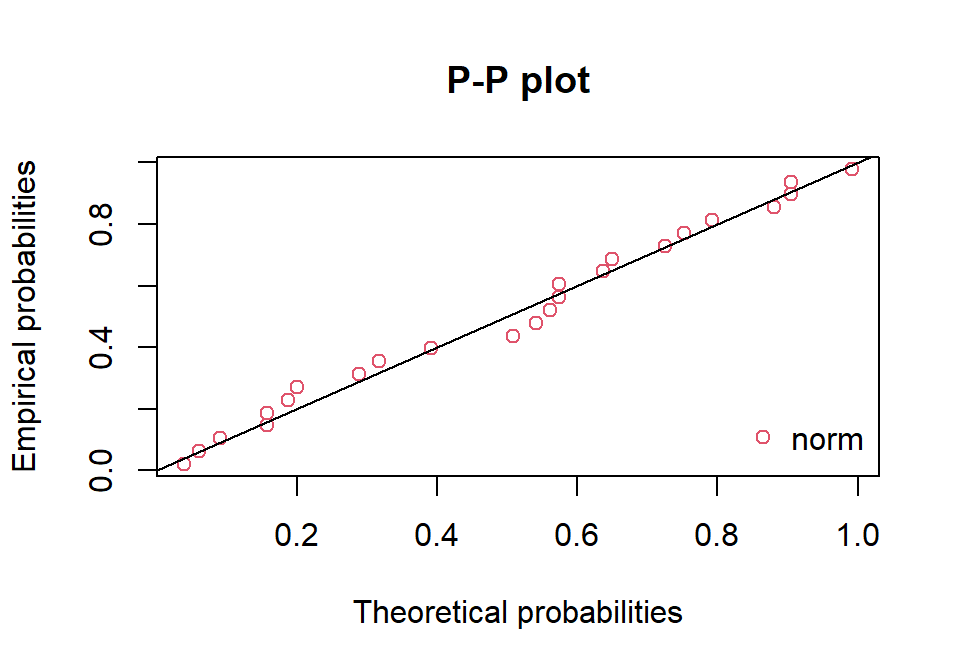
Pav. 16.10: PP diagramos pavyzdys.

16.4.3 Kitų tipų grafikai

Teorinį ir empirinį pasiskirstymą galima lyginti ir pagal kito tipo grafikus, pvz.:

empirines histogramas lyginti su teorine tikimybės tankio kreive (pav. 16.11);
empirinį branduolių tankį su teoriniu tikimybės tankiu;
empirinius sukauptuosius santykinius dažnius ir teorinio normaliojo pasiskirstymo funkciją (pav. 16.12).

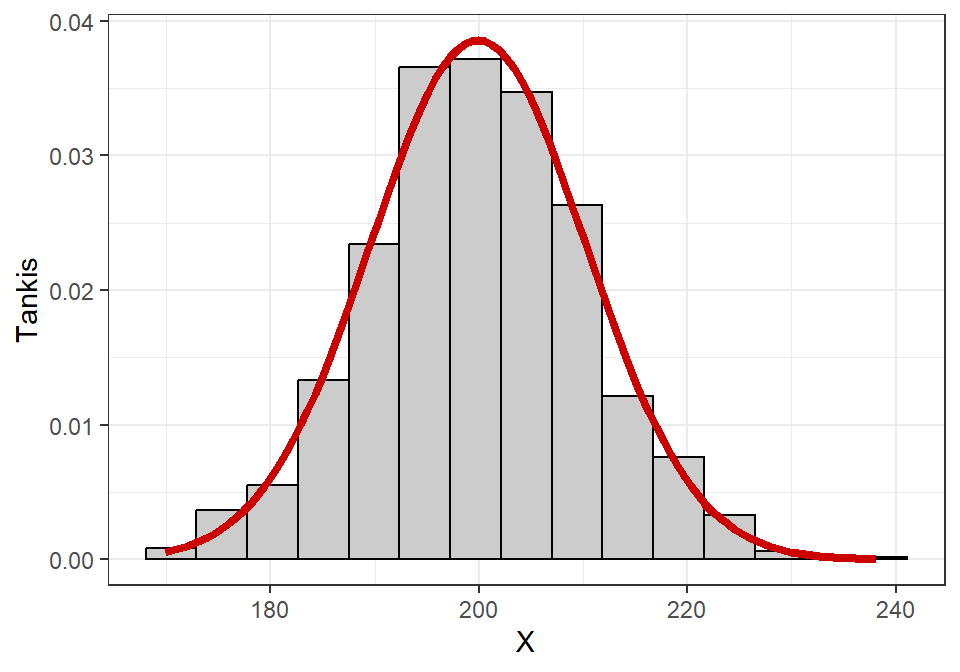
Grafiko, kuriame lyginama teorinė normaliojo tankio kreivė (raudona linija) ir empirinė histograma.
Iššūkis braižant šio tipo grafiką – histogramos stulpelių aukštį paversti į tankio vienetų matavimo skalę.

Pav. 16.11: Grafiko, kuriame lyginama teorinė normaliojo tankio kreivė (raudona linija) ir empirinė histograma. Iššūkis braižant šio tipo grafiką – histogramos stulpelių aukštį paversti į tankio vienetų matavimo skalę.

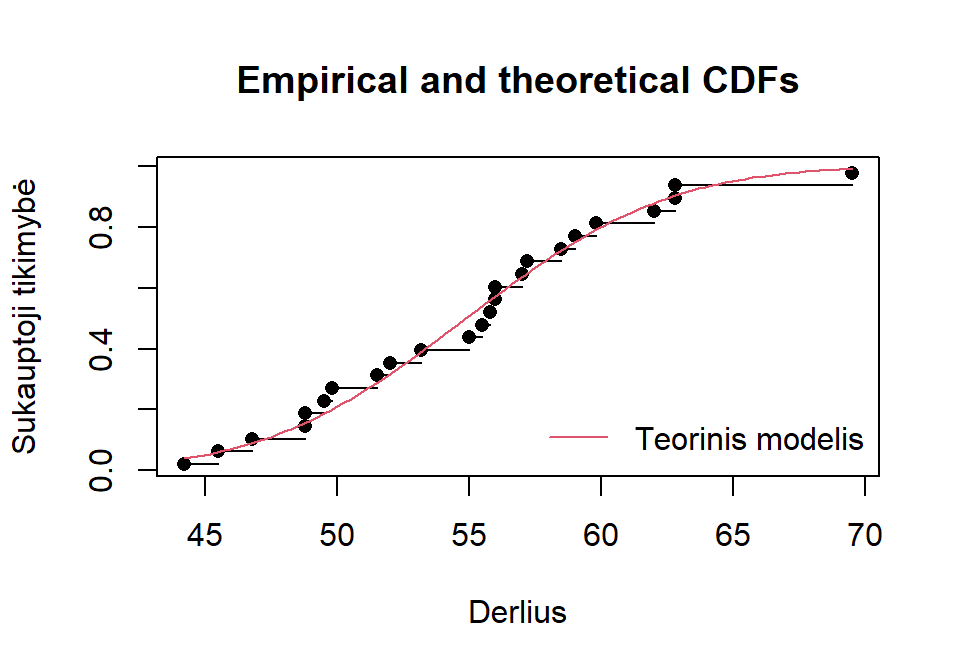
Grafiko, kuriame lyginama teorinė (raudona linija) ir empirinė (juodi taškai) kreivės, pavyzdys.
$CDF$ -- tikimybių pasiskirstymo funkcija (angl. *cumulative distribution function*).

Pav. 16.12: Grafiko, kuriame lyginama teorinė (raudona linija) ir empirinė (juodi taškai) kreivės, pavyzdys. $CDF$ – tikimybių pasiskirstymo funkcija (angl. cumulative distribution function).

Skirtumo tarp šių dviejų (pasiskirstymo ir sukauptųjų santykinių dažnių) funkcijų reikšmingumą lygina Lilliefor’o/Kolmogorovo-Smirnovo kriterijus normalumui tikrinti (pastaba: šis kriterijus yra ganėtinai konservatyvus).

16.5 Transformacijos

Jei duomenų pasiskirstymas atrodo nukrypęs nuo normalumo, galima bandyti įvairias transformacijas – logaritmavimą ($Y' = ln(Y)$), šaknies traukimą ($Y' =\sqrt{Y}$), kėlimą laipsniu, Box-Cox ar kitokias transformacijas (Čekanavičius ir Murauskas 2004, p.7; McDonald 2014e; McDonald 2014k) – ir normalumo tikrinimą kartoti jau transformuotiems duomenims. Tačiau transformacijos padeda ne visada. Be to, kuo sudėtingesnė transformacija, tuo sunkiau gautus rezultatus interpretuoti.

16.6 Rezultatų aprašymas: normalumas

Kriterijus įprastai taikomas kaip prielaidų tikrinimo metodas, tad užtenka teigti, kad, pvz., „normalumo prielaida tikrinta Shapiro-Wilk kriterijumi ir kvantilių palyginimo diagrama“ bei „normalumo prielaida buvo tenkinama“ arba „visos modeliui keliamos prielaidos buvo tenkinamos“, arba „normalumo prielaida buvo pažeista, todėl… (darėme tą ir aną)“.

Informacijos šaltiniai

Čekanavičius V., Murauskas G. Statistika ir jos taikymai II. Vilnius: TEV (2004).

Clapham M.E. 9: Shapiro-Wilk test (2016). Prieiga per internetą: https://youtu.be/dRAqSsgkCUc.

Field A. An Adventure in Statistics: The Reality Enigma. London: Sage (2016). Prieiga per internetą: https://us.sagepub.com/en-us/nam/discovering-statistics/book237529.

McDonald J.H. Data transformations. Handbook of Biological Statistics. Baltimore, Maryland: Sparky House Publishing. (2014e). Prieiga per internetą: http://www.biostathandbook.com/transformation.html.

McDonald J.H. Normality. Handbook of Biological Statistics. Baltimore, Maryland: Sparky House Publishing. (2014k). Prieiga per internetą: http://www.biostathandbook.com/normality.html.

Shapiro S.S., Wilk M.B. An analysis of variance test for normality (complete samples), Biometrika 52(3-4): 591–611 (1965). DOI: 10.1093/biomet/52.3-4.591.

Wilk M.B., Gnanadesikan R. Probability plotting methods for the analysis for the analysis of data, Biometrika 55(1): 1–17 (1968). DOI: 10.1093/biomet/55.1.1.