15. Ryšys tarp kategorinių kintamųjų

Sąsaja ir nepriklausomumas – tai labai susijusios sąvokos: jei du požymiai (kategoriniai kintamieji)¹⁰ yra susiję, vadinasi, priklausomi. Jei sąsajos nenustatome – gali būti visaip: ir priklausomi, ir nepriklausomi. Iš principo, šiame poskyryje mokysimės tirti, ar sąsaja tarp kategorinių kintamųjų yra statistiškai reikšminga, ir įvertinti jos stiprumą.

15.1 Dažnių lentelės sudarymas

Įprastinė veiksmų seka tiriant kategorinius kintamuosius:

(dažnių lentelė ir prielaidų tikrinimas) sudaroma ir paanalizuojama dažnių lentelė,
(statistinis reikšmingumas) pagal ją nusprendžiama, kokiu būdu reikia tikrinti statistinį sąsajos reikšmingumą,
(efekto dydis) patikrinus reikšmingumą, pasirenkamas metodas sąsajos stiprumui vertinti,
įvykdžius minėtąsias analizes, padaroma galutinė išvada.

Išskyrus tai, kad sudaroma dažnių lentelė, principas lieka toks pats, kaip koreliacinės analizės metu. Tik ryšio reikšmingumas ir stiprumas skaičiuojami naudojant atskiras funkcijas.

Kategorinių duomenų analizės principas: pirma susidarome dažnių lentelę ir toliau kitomis funkcijomis analizuojame šią lentelę.

Duomenys analizei gali būti pateikti dviem formomis:

kaip duomenų lentelė, kurioje yra 2 kategoriniai (ar diskretieji) kintamieji (lentelė 15.1);
kaip dažnių lentelė (lentelė 15.2).

Lentelė 15.1: Ryšiui tarp 2 kategorinių kintamųjų reikalinga duomenų struktūra 1: lentelė su 2 kategoriniais (diskrečiaisiais) kintamaisiais.
Kintamasis 1	Kintamasis 2
A	Katinas
B	Katinas
C	Katinas
A	Papūga
B	Papūga

Lentelė 15.2: Ryšiui tarp 2 kategorinių kintamųjų reikalinga duomenų struktūra 2: porinė dažnių lentelė.
	Katinas	Papūga
A	3	8
B	4	3
C	12	2

15.2 Aprašomoji statistika ir grafikai

Sudarytą absoliučiųjų dažnių lentelę galime pasiversti į išplėstinę dažnių lentelę ir ją paanalizuoti.

                     Katinas   Papūga    (Suma)
                                       
A       Dažnis             3        8       11
        % bendras       9.4%    25.0%    34.4%
        % eilut.       27.3%    72.7%        .
        % stulp.       15.8%    61.5%        .
                                       
B       Dažnis             4        3        7
        % bendras      12.5%     9.4%    21.9%
        % eilut.       57.1%    42.9%        .
        % stulp.       21.1%    23.1%        .
                                       
C       Dažnis            12        2       14
        % bendras      37.5%     6.2%    43.8%
        % eilut.       85.7%    14.3%        .
        % stulp.       63.2%    15.4%        .
                                       
(Suma)  Dažnis            19       13       32
        % bendras      59.4%    40.6%   100.0%
        % eilut.           .        .        .
        % stulp.           .        .        .

Taip pat rezultatus galime atvaizduoti mozaikine (pav. 15.1) ar stulpeline diagrama.

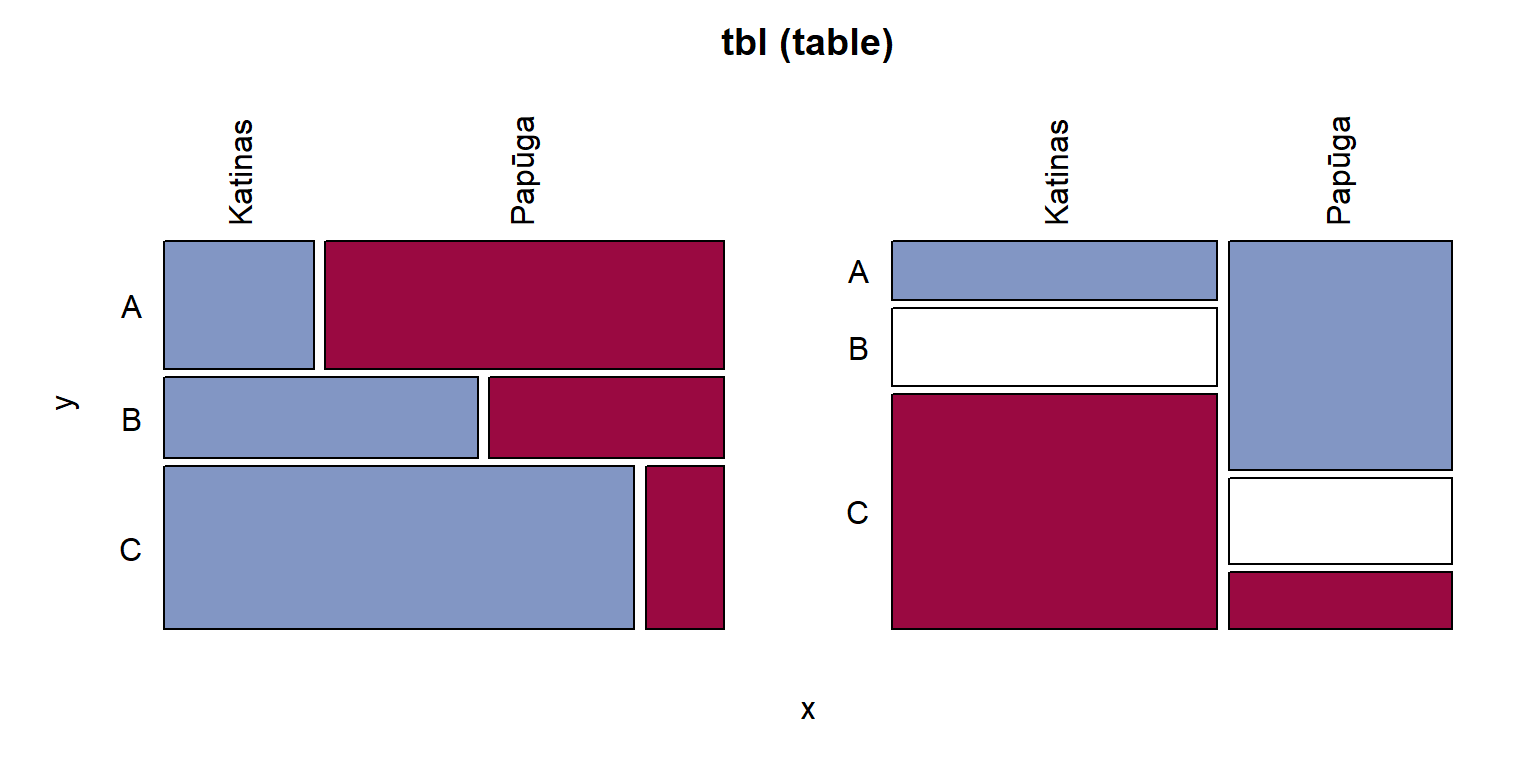
Pav. 15.1: Mozaikine diagrama atvaizduota porinė dažnių lentelė.

15.3 Statistinis reikšmingumas

Tradiciškai statistikoje uždavinys nustatyti, ar ryšys tarp kategorinių kintamųjų yra statistiškai reikšmingas, vadinamas požymių nepriklausomumo (angl., independence) tikrinimu. Tam gali būti naudojamas vienas iš šių kriterijų:

Fišerio tikslusis kriterijus. Šis kriterijus įprastai taikomas imtims, mažesnėms nei 1000, nes kitu atveju skaičiavimai gali užtrukti ilgai (McDonald 2014g). Taip pat tais atvejais, kai nekorektiška naudoti \(\chi^2\) (chi kvadratu) ar \(G\) požymių nepriklausomumo kriterijus. Tarkim, kai kažkurių pogrupių dažniai (dažnių lentelės langelių reikšmės) mažesni kaip 5.
Pirsono \(\chi^2\) kriterijus. \(\chi^2\) požymių nepriklausomumo kriterijus laikomas tinkamu naudoti, kai imties dydis yra bent 30, o 75% dažnių lentelės langelių teorinis (tikėtinas) dažnis yra 5 arba daugiau (Čekanavičius ir Murauskas 2006). Įprastai taikomas, kai imtis didesnė už 1000, nes mažoms imtims tikslesnis Fišerio tikslusis kriterijus (McDonald 2014b). Plačiau apie \(\chi^2\) tinkamumą skaitykite vadovėliuose (Čekanavičius ir Murauskas 2006, p.213–214) bei (McDonald 2014b).
\(G\) kriterijus (tikėtinumų santykio kriterijus). Toms pačioms situacijoms, kur tinka \(\chi^2\) kriterijus, kai kurie autoriai rekomenduoja taikyti tikėtinų santykio, t.y., \(G\) kriterijų (McDonald 2014i). \(G\) kriterijus įprastai naudojamas, kai imties dydis didesnis nei 1000, nes kitu atveju tikslesniu laikomas Fišerio tikslusis kriterijus (McDonald 2014i).

Kurį kriterijų – \(\chi^2\) ar \(G\) – rinktis, dažnai yra skonio dalykas, nes, nors \(G\) turi geresnes matematines savybes, o \(\chi^2\) – geriau žinomas, abu įprastai duoda labai panašius rezultatus. Daugiau aiškumo apsispręsti įneš ši pastraipa „Chi-square vs. G–test“ .

\(\chi^2\) bei \(G\) kriterijų statistikos yra apibrėžtos lygtimis (13.1) ir (13.2). Kai imtis didelė, tiek viena, tiek kita statistika skirstosi pagal \(\chi^2\) skirstinį su \((r-1)(c-1)\) laisvės laipsnių, kur \(r\) ir \(c\) atitinkamai pirmojo ir antrojo kategorinio kintamojo kategorijų skaičius.

Atkreipkite dėmesį, kad aptartieji kriterijai gali padėti atsakyti į klausimą „Ar tikėtina, kad požymiai susiję?“ (visgi, savo išvadas grįsti vien tik \(p\) reikšmėmis yra bloga praktika), bet neatsako – „Kaip labai? Koks sąsajos stiprumas?“ (dar reiktų išsiaiškinti efekto dydį, t.y., sąsajos stiprumą). Apie tai – kitame poskyryje.

15.4 Efekto dydis

Efekto dydį (t.y., ryšio stiprumą) galime įvertinti naudodami vieną iš kelių galimų kategorinių kintamųjų ryšio matų (apie šiuos koeficientus plačiau rašoma (Čekanavičius ir Murauskas 2006, p.216–221), (Mangiafico 2016b)). Juos galima suskirstyti į kelias grupes:

\(\chi^2\) statistika pagrįsti ryšio stiprumo matai;
Prognozavimo klaidos sumažėjimą parodantys matai;
Kiti.

15.4.1 \(\chi^2\) statistika pagrįsti ryšio stiprumo matai

Panagrinėkime tris (visais atvejais nulis rodo, kad sąsajos nėra) šio tipo atstovus:

Koeficientas \(\phi\) (Phi-Coefficient) – tarpusavio sutapimo rodiklis. Skaičiuojamas tik \(2 \times 2\) dažnių lentelėms. Kinta nuo 0 iki 1.
Kontingencijos koeficientas (Contingency Coeff.). Niekada neviršija 1. Didžiausia reikšmė priklauso nuo dažnių lentelės stulpelių ir eilučių skaičiaus.
Kramerio koeficientas \(V\) (Cramer's V). Kinta nuo 0 iki 1. \(2 \times 2\) dažnių lentelei koeficientai \(V\) ir \(\phi\) sutampa \((V = \phi)\). Koeficiento \(V\) apibrėžimas pateiktas išraiškoje (15.1), o tikslesnė jo skaitinės reikšmės interpretacija priklauso nuo analizuojamų grupių skaičiaus. Ji pateikta lentelėje 15.3. Reiktų žinoti, kad klasikinis \(V\) koeficientas yra paslinktasis – dažnai rodo stipresnį ryšio stiprumą, nei tas stiprumas yra. Todėl rekomenduojama naudoti koreguotąją/nepaslinktąją koeficiento versiją (Bergsma 2013).

\[\begin{equation} V = \sqrt{\frac{\chi^2/n}{min(k-1; r-1)}} \tag{15.1} \end{equation}\]Čia \(\chi^2\) (chi kvadratu) yra išraiškos (4.18) arba (13.1) rezultatas, \(n\) – imties dydis, \(r\) ir \(k\) – dažnių lentelės eilučių ir stulpelių skaičius.

Sąsajos tarp kategorinių kintamųjų stiprumui (efekto dydžiui) įvertinti siūlau naudoti (koreguotąjį) Kramerio \(V\).

15.4.2 Kramerio V koeficiento interpretacija

Kramerio V koeficientas iš aptartųjų yra panašiausias į koreliacijos koeficientus: kai jo reikšmė lygi nuliui – sąsajos nėra, kai reikšmė lygi 1 – visiška priklausomybė tarp kategorinių kintamųjų. Visgi tarpinių reikšmių interpretacija (kaip ir koreliacijos atveju) labai priklauso nuo mokslų srities, kuriai atliekama analizė, ir analizės tikslų. Pvz., Cohen (Kohenas) 1988 metais pateikė tokias gaires elgsenos (ne gamtos!) mokslams, kurios nurodytos 15.3 lentelėje. Tad kaip pastebite, interpretacija gali priklausyti ir nuo kategorijų skaičiaus.

Lentelė 15.3: Sąlyginė **Kramerio V** koeficiento interpretacija pagal Cohen (elgsenos mokslams). Šaltinis: (Mangiafico 2016b).
Efekto dydis	„mažas“	„vidutinis“	„didelis“
min. k = 2	0.10 – < 0.30	0.30 – < 0.50	≥ 0.50
min. k = 3	0.07 – < 0.20	0.20 – < 0.35	≥ 0.35
min. k = 4	0.06 – < 0.17	0.17 – < 0.29	≥ 0.29

Žymėjimai: min. k – mažiausias kategorijų skaičius dažnių lentelės eilutėse arba stulpeliuose.

15.4.3 Prognozės klaidos sumažėjimą rodantys matai

Šios klasės matų pavyzdžiai – Goodman-Kruskal \(\lambda\) bei Goodman-Kruskal \(\tau\) koeficientai, ¹¹˒ ¹² kurie matuoja tą patį dalyką, tik skaičiuojami kitaip. Jų interpretacija: 0 – klaidos sumažėjimas yra 0% palyginus su atsitiktiniu spėjimu, 1 – klaidos sumažėjimas yra 100%. T.y., labai aiški interpretacija. Koeficientas \(\lambda\) turi blogą savybę, kad kai kuriose situacijose grynai dėl to, kaip jis skaičiuojamas, gaunama reikšmė lygi 0, nors realiai ji turėtų būti didesnė už nulį. Todėl labiau rekomenduočiau naudoti \(\tau\).

15.4.4 Kiti efekto dydžio matai

Kaip efekto dydžiai ypač epidemiologijoje dažnai naudojami santykinė rizika (angl. relative risk)¹³ ar galimybių (šansų) santykis (angl. odds ratio)¹⁴. Kitose srityje gali būti naudojami entropijos koeficientas (angl. coefficient of uncertainty) ir kitokie matai.

15.5 Rezultatų aprašymas: ryšys tarp kategorinių kintamųjų

Aprašant sąsajos tarp dviejų kategorinių kintamųjų analizės rezultatus trumpai nurodoma, kas analizuota, apibūdinami analizuojami požymiai. Taip pat pateikiami tikslūs analizės metodų pavadinimai: tas, kuriuo tirtas sąsajos statistinis reikšmingumas, ir tas, kuriuo įvertintas sąsajos stiprumas. Pateikiama \(p\) reikšmė (įprastai 3 skaitmenų po kablelio tikslumu) ir sąsajos stiprumą apibūdinantis koeficientas (įprastai užtenka 2 skaitmenų po kablelio). Grafiškai rezultatai atvaizduojami tinkama mozaikine arba stulpeline diagrama.

Rezultatus galime aprašyti taip: „Ryšys tarp gyvūnų rūšies ir viruso tipo yra statistiškai reikšmingas, bet silpnas (Fišerio tikslusis kriterijus, \(p\) = 0,009, Kramerio V = 0,17).“

15.6 Rekomenduojami informacijos šaltiniai

Šiame konspekte pateikti tik esminiai sąsajos tarp kategorinių kintamųjų aspektai. Išsamiau teorija išdėstyta vadovėliuose (Čekanavičius ir Murauskas 2006, p.197–223) bei anglų kalba (McDonald 2014b; McDonald 2014g; McDonald 2014i). Praktinių pavyzdžių pateikta šiuose šaltiniuose: (Mangiafico 2016a), (Mangiafico 2016b).

Informacijos šaltiniai

Bergsma W. A bias-correction for Cramér’s V and Tschuprow’s T, J. Korean Stat. Soc. 42(3): 323–328 (2013). DOI: 10.1016/j.jkss.2012.10.002.

Čekanavičius V., Murauskas G. Statistika ir jos taikymai I. Vilnius: TEV (2006).

Mangiafico S.S. Association Tests for Nominal Variables. Summary and Analysis of Extension Program Evaluation in R. New Brunswick, NJ: Rutgers Cooperative Extension. (2016a). Prieiga per internetą: https://rcompanion.org/handbook/H_04.html.

Mangiafico S.S. Measures of Association for Nominal Variables. Summary and Analysis of Extension Program Evaluation in R. New Brunswick, NJ: Rutgers Cooperative Extension. (2016b). Prieiga per internetą: http://rcompanion.org/handbook/H_10.html.

McDonald J.H. Chi-square test of independence. Handbook of Biological Statistics. Baltimore, Maryland: Sparky House Publishing. (2014b). Prieiga per internetą: http://www.biostathandbook.com/chiind.html.

McDonald J.H. Fisher’s exact test of independence. Handbook of Biological Statistics. Baltimore, Maryland: Sparky House Publishing. (2014g). Prieiga per internetą: http://www.biostathandbook.com/fishers.html.

McDonald J.H. G–test of independence. Handbook of Biological Statistics. Baltimore, Maryland: Sparky House Publishing. (2014i). Prieiga per internetą: http://www.biostathandbook.com/gtestind.html.