1. Pradinės sąvokos

1.1 Statistika ir biostatistika

Statistiką galima apibūdinti kaip tikslųjį mokslą apie tyrimų planavimą (bent jau statistinius planavimo aspektus), duomenų rinkimą, sisteminimą, analizę ir gautų rezultatų interpretavimą (Bagdonavičius ir Kruopis 2015; Čekanavičius ir Murauskas 2006). Pačią statistiką galima suskirstyti į matematinę bei taikomąją. Pagrindinis matematinės statistikos dėmesys nukreiptas į matematikos ir tikimybių teorijos principus, statistikos teorijos ir metodų plėtrą bei tyrimus. Tai labiau teorinė, labiau abstrakti sritis, kuriai konkretūs tyrimo objektai ar konkrečios praktinio pritaikymo sritys mažiau svarbios. Tuo tarpu taikomoji statistika statistikos teoriją priartina prie tam tikros srities – žemės ūkio, inžinerijos, sporto, medicinos, kultūros, socialinių mokslų ar kitos – bei taiko statistikos principus šios srities problemoms spręsti (Martišius ir Kėdaitis 2013). Kai kurios taikomosios statistikos sritys netgi turi specifinius pavadinimus: psichologijos tyrimų metodologija ir statistika – psichometrija, ekonomikos statistika – ekonometrija, cheminių sistemų statistika – chemometrija, biomokslų (biologijos, genetikos, medicinos ir kitų bio sričių) statistika – biostatistika.

1.2 Statistikos dalys

Statistikos metodus galima suskirstyti į kelias pagrindines dalis:

1. Tyrimo planavimas – prieš vykdant tyrimą, visa jo eiga turi būti kruopščiai suplanuojama. Norint tinkamai suplanuoti tyrimą, reikia tiek specialybės srities (pvz., biologijos, genetikos), tiek statistikos žinių. Specialybinės tiriamos srities žinios nėra statistikos mokslo objektas, tad čia reikalingas tos srities ekspertas. Tačiau statistiniai aspektai yra, todėl čia taip pat reikalingas ir reikiamų statistikos žinių turintis ekspertas. Šio etapo metu suformuluojama tiriamoji problema, apibrėžiama, kas yra tyrėją dominantys tiriamieji ar objektai, nusprendžiama, kaip bus sudaroma tinkama tiriamųjų imtis, kokios savybės bus ištiriamos, kaip bus renkami duomenys, numatoma, kokios analizės metodų grupės bus naudojamos. Nuo to priklauso reikiamas tiriamųjų skaičius bei kitos subtilybės. Jei tyrimas prastai suplanuotas ar duomenų surinkimo stadija prastai įvykdyta, mažai tikėtina, kad kitos tyrimo ir duomenų analizės dalys atsvers šiuos trūkumus. Tad planavimui privalo būti skiriamas prideramas dėmesys.
2. Aprašomoji statistika (angl. descriptive statistics) – grafiniai ir skaitiniai duomenų sisteminimo metodai. Jais glaustai apibūdiname esmines surinktų duomenų savybes, o tai padeda gauti įžvalgų apie duomenis, interpretuoti rezultatus. Deja, aprašomosios statistikos metodai neįvertina paklaidų ir gautų rezultatų patikimumo (statistinio reikšmingumo), todėl įprastai reikalingi tolimesni analizės etapai. Visgi pagal šio etapo rezultatus pasirenkama ar patikslinama tolimesnė analizės eiga.
3. Statistinės išvados (angl. inferential statistics) – tai pagal imties duomenis padarytos išvados apie visą generalinę aibę (GA). Šio etapo metu vertinamos paklaidos bei rezultatų statistinis reikšmingumas. Statistinių išvadų darymas yra grindžiamas tikimybių teorijos dėsniais ir aksiomomis. Tad tam, kad būtų įmanoma įvertinti paklaidas ir išvados būtų korektiškos, imtis turi būti sudaryta tinkamai. Tai pasiekiama tik gerai suplanavus ir tinkamai įvykdžius tyrimą.

Pav. 1.1 („centrinė statistikos dogma“ ) vaizduoja, kaip susijusios tikimybių teorija, aprašomoji statistika ir statistinių išvadų darymas.

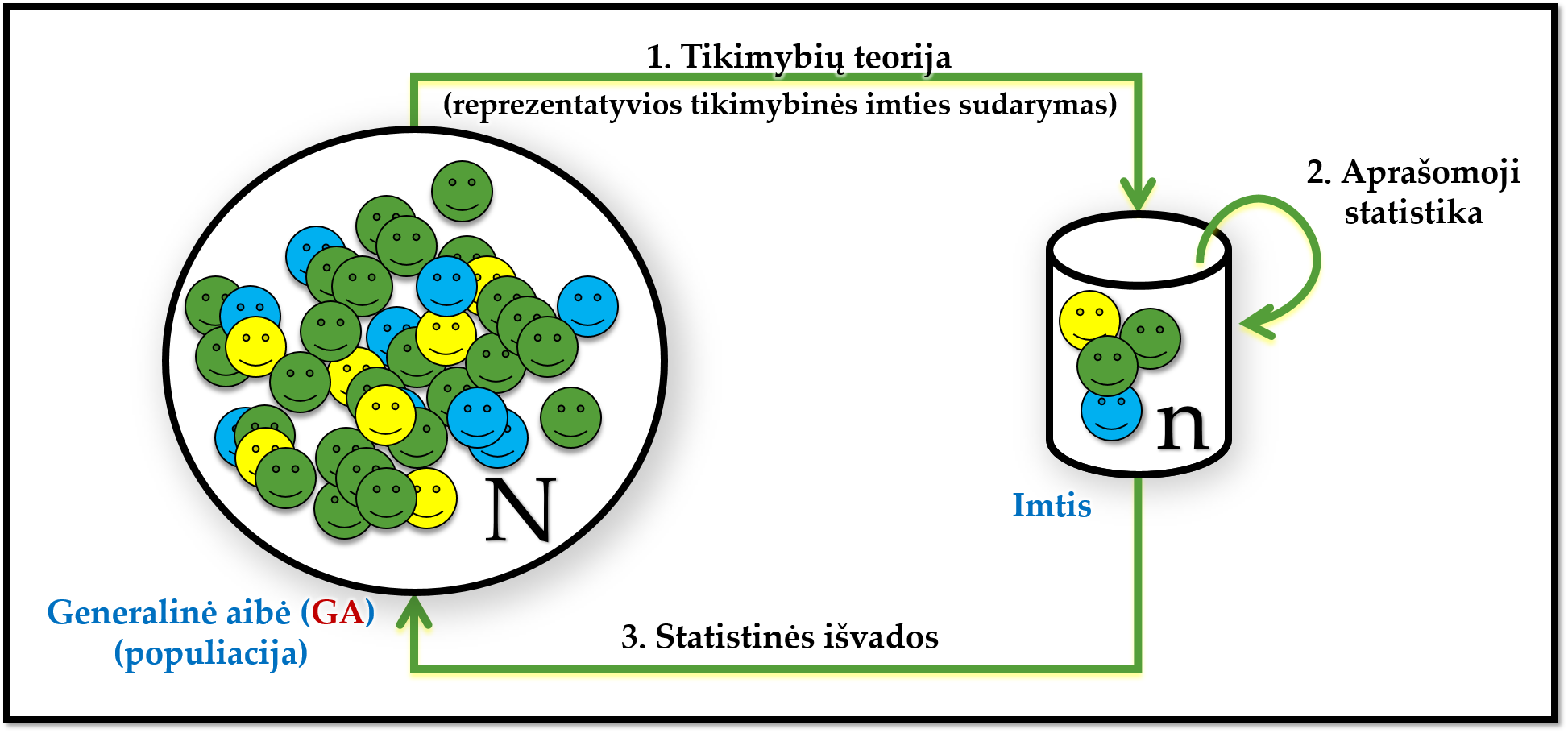
Pav. 1.1: Sąsaja tarp tikimybių teorijos, aprašomosios statistikos bei statistinių išvadų darymo.

Kiekviena iš šių dalių plačiau bus nagrinėjama atskiruose skyriuose. O dabar aptarkime kelias svarbiausias sąvokas.

1.3 Generalinė aibė, imtis ir duomenys

Statistikoje yra keli svarbūs pradiniai terminai: generalinė aibė (populiacija), imtis bei duomenys (pav. 1.2).

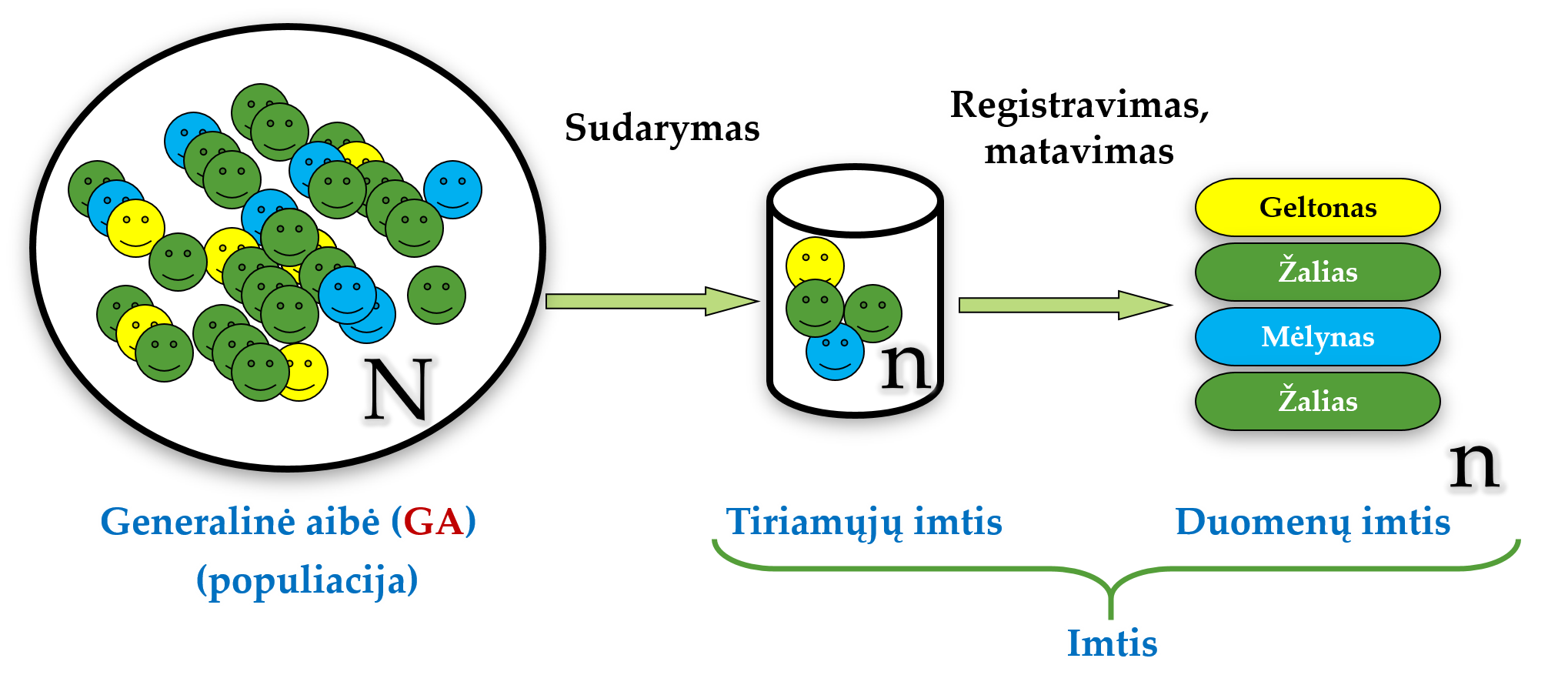
Pav. 1.2: Generalinė aibė, imtis ir duomenys. Iš visos tyrimo metu analizuojamos objektų visumos (generalinės aibės, GA) visiškai atsitiktinai arba kitu tikimybiniu būdu sudarome tiriamųjų imtį (paimame dalį GA). Tada išmatuojame ar užregistruojame vieną arba kelis mus dominančius tiriamųjų požymius ir taip gauname duomenis (duomenų imtį).

Generalinė aibė (GA), arba populiacija (statistikos prasme),– tai statistinio tyrimo metu tyrėją dominanti objektų visuma. Pvz., visi diabetikai.

Imtis – tai į tyrimą patekusi GA dalis (į tyrimą patekę tiriamieji ar objektai). Pvz., tik tie diabetikai, apie kuriuos surinkome duomenis.

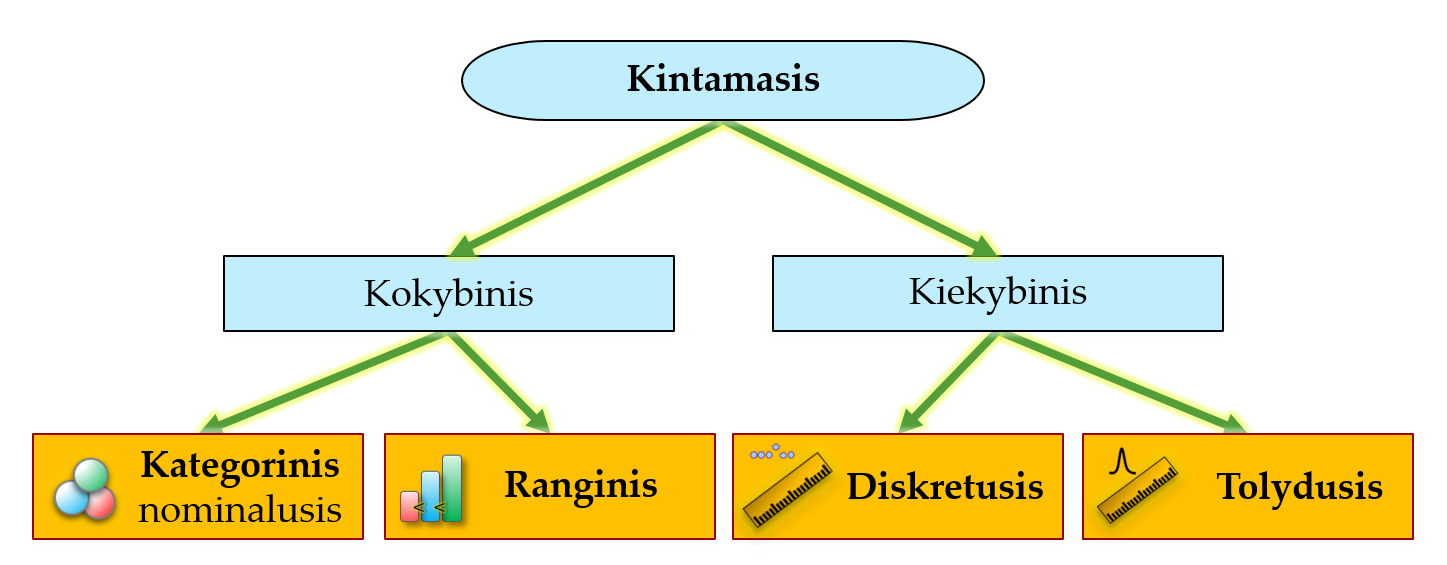
Duomenys – tai imties narių (tiriamųjų, objektų) savybių reikšmės. Savybės gali būti kokybinės (pvz., spalva) bei kiekybinės (pvz., svoris gramais).

Imties dydis – tai imtyje esančių elementų (objektų, tiriamųjų, stebėjimų) skaičius. Pvz., ištirtų diabetikų skaičius.

Pavyzdys. GA – tai visi 4-5 m. amžiaus naminiai šunys, imtis – tai į tyrimą patekę 4-5 m. amžiaus naminiai šunys, duomenys – į tyrimą patekusių šunų kailio spalva: šviesi, tamsi, marga, …

Statistiniam tyrimui tinkama imtis turėtų būti reprezentatyvi, tikimybinė ir pakankamo dydžio.

• Reprezentatyvi imtis yra tokia, kurioje pakankamai tiksliai atsispindi visos tyrimui svarbios GA savybės. Tai pagal tam tikrų savybių reikšmių pasiskirstymą yra tarsi maža GA kopija. Imtis turi būti reprezentatyvi tai GA, apie kurią daromos statistinės išvados (kartais duomenis surenkame netinkamu būdu, todėl jie neatspindi mus dominančios GA savybių – taip galim apgauti patys save), nes kitaip išvados bus klaidingos, jas nekorektiška apibendrinti visai GA. T.y., jei imtyje yra tik vyresni nei 60 m. amžiaus vyrai, tai didelis klausimas, ar ištyrę juos galime daryti išvadas apie visus žmones, tarp kurių yra ir moterys, vaikai, kūdikiai bei jaunimas.
• Tikimybinė imtis yra sudaryta pagal tikimybių teorijos principus: atsitiktinumas yra griežtai apibrėžtas ir kiekvienam GA elementui yra žinoma tikimybė patekti į imtį. Jei atsitiktinumas yra griežtai apibrėžtas, tai jį galime įvertinti, pvz., skaičiuodami paklaidas. Jei atsitiktinumas nėra griežtai apibrėžtas, tai jo įvertinti negalime, tad ir paklaidas skaičiuoti ar daryti apibendrinančias išvadas yra beprasmiška.
• Pakankamo dydžio. Per mažo dydžio imtys yra nereprezentatyvios ir iš jų padarytos išvados, tikėtina, bus klaidingos. Vien tik didelis imties dydis irgi pats savaime negarantuoja reprezentatyvumo, jei imtis sudaryta netinkamu būdu (pvz., jei yra netikimybinė).

Kelios pastabos:

• Atkreipkite dėmesį į tai, kad terminas „populiacija“ statistikoje reiškia ne tą patį, ką biologijoje, ekologijoje ar demografijoje, todėl, vengiant dviprasmybės, lietuvių kalba yra aprobuotas kitas statistinis terminas („populiacijos“ sinonimas) – generalinė aibė (GA).
• Terminas „imtis“ gali reikšti ir tiriamųjų imtį (pvz., į tyrimą įtraukti 4-5 m. amžiaus naminiai šunys), ir duomenų imtį (pvz., tyrimo metu užregistruota kiekvieno iš šių šunų kailio spalva). Tikiuosi, dėl to problemų nekils.

Plačiau su temomis apie statistinių duomenų tipus galite susipažinti vadovėliuose (Čekanavičius ir Murauskas 2006; McDonald 2014m).

1.4 Duomenų tipai statistikoje

Statistikoje kintamaisiais vadinamos tiriamųjų savybės. Duomenų analizės metodo pasirinkimas labai smarkiai priklausys nuo kintamojo prigimties. Pagal prigimtį statistiniai kintamieji skirstomi į 2 dideles grupes: kokybinius (kategorinius plačiąja prasme) ir kiekybinius. Šie, savo ruožtu, skaidomi į 4 pagrindinius tipus (pav. 1.3). Vieną kintamąjį sudaro to paties tipo duomenys, tad terminus „duomenų tipai“ ir „kintamųjų tipai“ naudosime kaip sinonimus.

Pav. 1.3: Pagrindiniai statistinių kintamųjų duomenų tipai.

• Kokybiniai (kategoriniai) kintamieji:
  • nominalieji (angl. nominal variable) – tai tokie kintamieji, kurių reikšmių (vadinamos kategorijomis) išdėstymo tvarka nesvarbi, t.y., reikšmės natūralios eilės tvarkos neturi. Matavimo vienetų irgi neturi. Pvz., ląstelės spalva – violetinė, raudona, melsva, bespalvė, – ląstelės forma – apvali, kvadratinė, pailga, netaisyklinga. Kartais kategorijos užkoduojamos skaičiais, pvz., 0 – sveikas, 1 – serga, bet dėl to kintamasis netampa kiekybiniu. Čia 0 ir 1 – tai tik kategorijų kodai, kurių eilės tvarka nesvarbi.
  • ranginiai (angl. ranked/ordered variable) – tai tokie kintamieji, kurių reikšmės (vadinamos kategorijomis) turi natūralią didėjimo ar mažėjimo tvarką, tačiau atstumas tarp gretimų reikšmių nėra pastovus ar tiksliai išmatuojamas. Įprastai matavimo vienetų neturi. Pvz., ląstelės dydžio kategorija – maža, vidutinė, didelė; savijauta – labai prasta, prasta, neutrali, gera, puiki. Ranginiams priklauso ir balais matuojami duomenys.
• Kiekybiniai kintamieji:
  • kiekybiniai diskretieji (angl. discrete variable) – tai tokie skaitiniai kintamieji, kurie yra suskaičiuojami. Jie turi baigtinį (suskaičiuojamą) galimų reikšmių skaičių ir atstumas tarp dviejų galimų gretimų reikšmių yra pastovus ir gali būti tiksliai išmatuotas. Paprasčiau sakant, kiekybiniai diskretieji kintamieji išreiškiami teigiamais ir neigiamais sveikaisiais skaičiais bei nuliu. Įprastai aprašo kieno nors skaičių, pvz., ląstelių skaičių, dantų skaičių, kėdžių skaičių, į paskaitą atėjusių studentų skaičių, sėkmingų bandymų skaičių, raudonų mėgintuvėlių skaičių;
  • tolydieji (angl. continuous variable) – tai skaitiniai kintamieji, kurie įprastai yra išmatuojami ar užregistruojami (bet ne suskaičiuojami). Gali įgyti ir trupmeniniais skaičiais užrašomas reikšmes (tarkim, 2,2354), teoriškai gali būti išmatuoti daugybės skaitmenų po kablelio tikslumu. Pasirinktame reikšmių intervale tarp dviejų skaičių (tarkim, tarp 2,2 ir 2,4) gali įgyti be galo daug reikšmių, nes skaitmenų po kablelio gali būti be galo daug. Įprastai turi konkrečius matavimo vienetus, nors gali būti išreikšti ir santykiniais vienetais ar būti bedimensiai dydžiai. Pvz., ląstelės svoris kilogramais, ilgis centimetrais, trukmė sekundėmis (kai skaičiuojamos ir sekundžių dalys), regėjimo aštrumas dioptrijomis, santykis tarp ilgio (metrais) ir pločio (metrais), šviesos intensyvumas santykiniais vienetais. Įprastai tokius skaičius suapvaliname iki tam tikro tikslumo tik dėl to, kad negalime išmatuoti be galo tiksliai arba praktiniam naudojimui užtenka ir mažesnio baigtinio tikslumo. Visgi teoriškai matuojamas kintamasis išlieka tolydusis.

1.5 Duomenų struktūros statistikoje

„Duomenų struktūra“ yra sąvoka, labiau siejama su darbu kompiuteriu nei su statistika. Visgi atliekant tyrimą svarbus dalykas yra nuspręsti, kokia forma rinksime, organizuosime ir saugosime duomenis. Mūsų pasirinkimas priklauso nuo tyrimo srities, sprendžiamo uždavinio ir duomenų rinkinio sudėtingumo. Šio kurso metu daugiausiai dirbsime su dviem formomis (duomenų struktūromis) – duomenų sekomis ir duomenų lentelėmis (duomenų sekomis, stulpeliais išdėliotomis į lentelės pavidalą) – tad siūlau skirti pakankamai daug laiko, kad tinkamai perprastumėte šias dvi struktūras.

1.5.2 Duomenų lentelė

Tvarkingosios duomenų lentelės – statistiniam tyrimui svarbiausia duomenų organizavimo forma. Ji yra standartizuota ir pritaikyta darbui statistinėmis programomis. Tvarkingos duomenų lentelės sudarymo principas: viena eilutė skirta vienam tiriamajam (ar vienam įrašui), vienas stulpelis – vienai savybei (kintamajam), o langeliuose – kiekvieno tiriamojo savybių reikšmės (žiūrėti pav. 1.4).

Pav. 1.4: Duomenų lentelės struktūra.

Atkreipkite dėmesį, kad stulpelių pavadinimai nurodo tiriamųjų savybes. Be to, lentelė turi turėti pavadinimą. Rekomenduojama lentelei suteikti prasmingą pavadinimą, kuris glaustai apibendrintų lentelėje surinktus duomenis ir/arba tyrimo esmę.

Duomenų lentelė gali būti gaunama vienos ar kelių duomenų sekų reikšmes surašius kaip stulpelius. Tik svarbu, kad pirma kiekvienos sekos reikšmė apibūdintų pirmą tiriamąjį, antra – antrąjį ir t.t. T.y., kad eilės tvarka atitiktų.

Terminas „tvarkingoji duomenų lentelė“ apibūdina duomenų pateikimo formą, bet neapibūdina turinio, pvz., ar duomenyse yra praleistų reikšmių.

Visgi, vykdant tyrimą, duomenis rekomenduoju rinkti iš karto duomenų lentelės pavidalu, papildomai pasidarant duomenų lentelės aprašymą. Aprašymas reikalingas tam, kad jūsų kolegos, vadovas arba jūs pats/pati po 6 mėnesių tiksliai žinotumėte, kokie duomenys šioje lentelėje. Aprašyme bent trumpai apibūdinkite tyrimą, jo tikslą, nurodykite duomenų rinkimo metodus ir prietaisus, pateikite kintamųjų aprašymą, kuriame nurodyti matavimo vienetai.

Rekomendacija: (1) surinktus duomenis iš karto surašykite į duomenų lentelės pavidalą ir (2) būtinai pasidarykite duomenų lentelės kintamųjų aprašymą.

Tvarkingųjų duomenų lentelių principai plačiau išdėstyti straipsnyje (Wickham 2014).

Užduotis 1.5

1. Kas yra tvarkingoji duomenų lentelė? Kas jos stulpeliuose ir kas – eilutėse?
2. Ar tvarkingojoje duomenų lentelėje gali būti praleistų reikšmių?
3. Išvardinkite 4 pagrindinius statistinei analizei svarbius duomenų tipus ir nurodykite bent po 2-3 jiems būdingas charakteristikas.
4. „Lenktynėse dalyvavo 8 žirgai. Juodi žirgai trasą įveikė per 3,2, 4,6 ir 4,0 min., šyvi – per 3,1 ir 4,2 min., bėri – per 3,9, 3,3, ir 4,1 min.“ Šioje pastraipoje pateiktą informaciją parašykite tvarkingosios duomenų lentelės pavidalu.